初中人教版12.3 角的平分线的性质当堂达标检测题

人教版2021年八年级上册：12.3 角的平分线的性质 课时练习

一．选择题

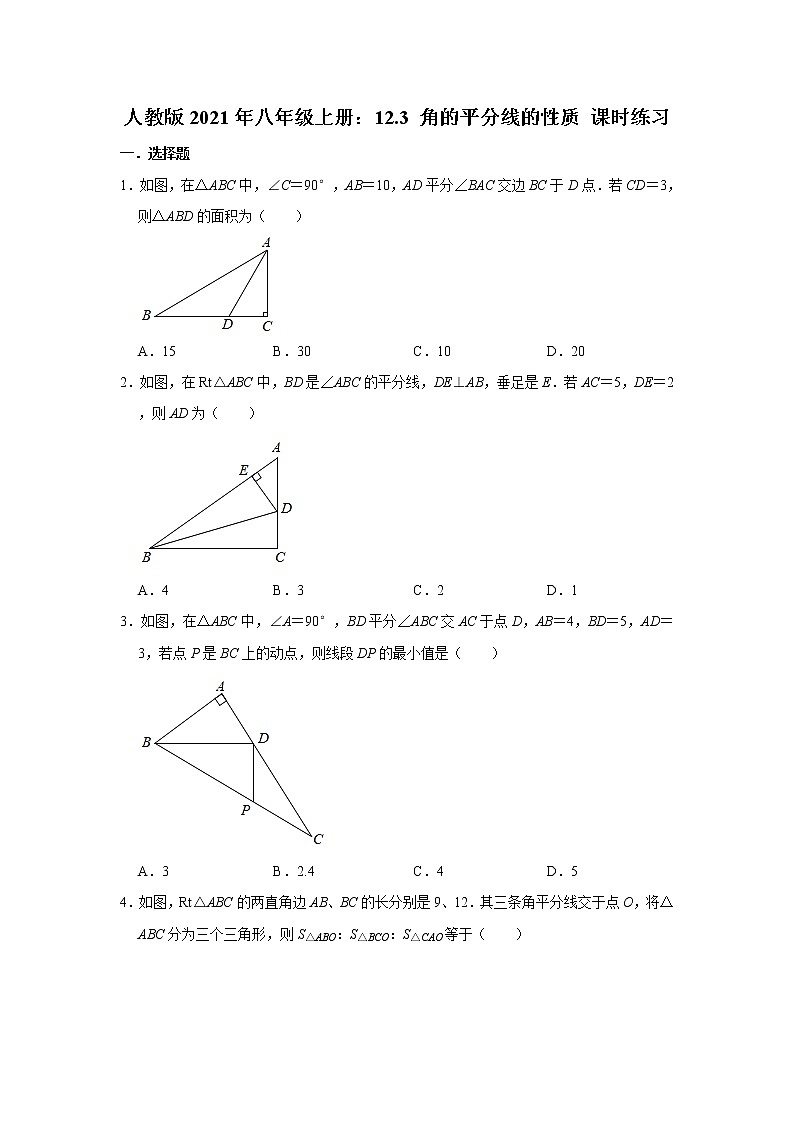
1．如图，在△ABC中，∠C＝90°，AB＝10，AD平分∠BAC交边BC于D点．若CD＝3，则△ABD的面积为（　　）

A．15 B．30 C．10 D．20

2．如图，在Rt△ABC中，BD是∠ABC的平分线，DE⊥AB，垂足是E．若AC＝5，DE＝2，则AD为（　　）

A．4 B．3 C．2 D．1

3．如图，在△ABC中，∠A＝90°，BD平分∠ABC交AC于点D，AB＝4，BD＝5，AD＝3，若点P是BC上的动点，则线段DP的最小值是（　　）

A．3 B．2.4 C．4 D．5

4．如图，Rt△ABC的两直角边AB、BC的长分别是9、12．其三条角平分线交于点O，将△ABC分为三个三角形，则S△ABO：S△BCO：S△CAO等于（　　）

A．1：1：1 B．1：2：3 C．3：4：5 D．2：3：4

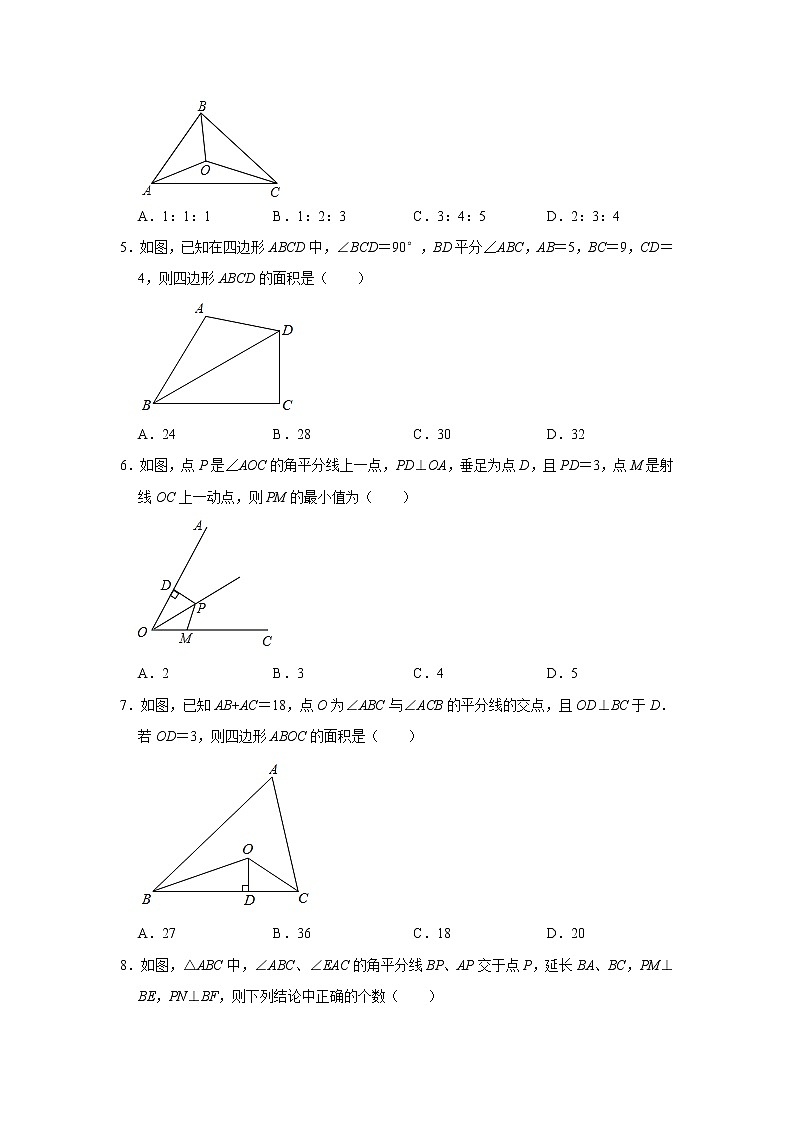
5．如图，已知在四边形ABCD中，∠BCD＝90°，BD平分∠ABC，AB＝5，BC＝9，CD＝4，则四边形ABCD的面积是（　　）

A．24 B．28 C．30 D．32

6．如图，点P是∠AOC的角平分线上一点，PD⊥OA，垂足为点D，且PD＝3，点M是射线OC上一动点，则PM的最小值为（　　）

A．2 B．3 C．4 D．5

7．如图，已知AB+AC＝18，点O为∠ABC与∠ACB的平分线的交点，且OD⊥BC于D．若OD＝3，则四边形ABOC的面积是（　　）

A．27 B．36 C．18 D．20

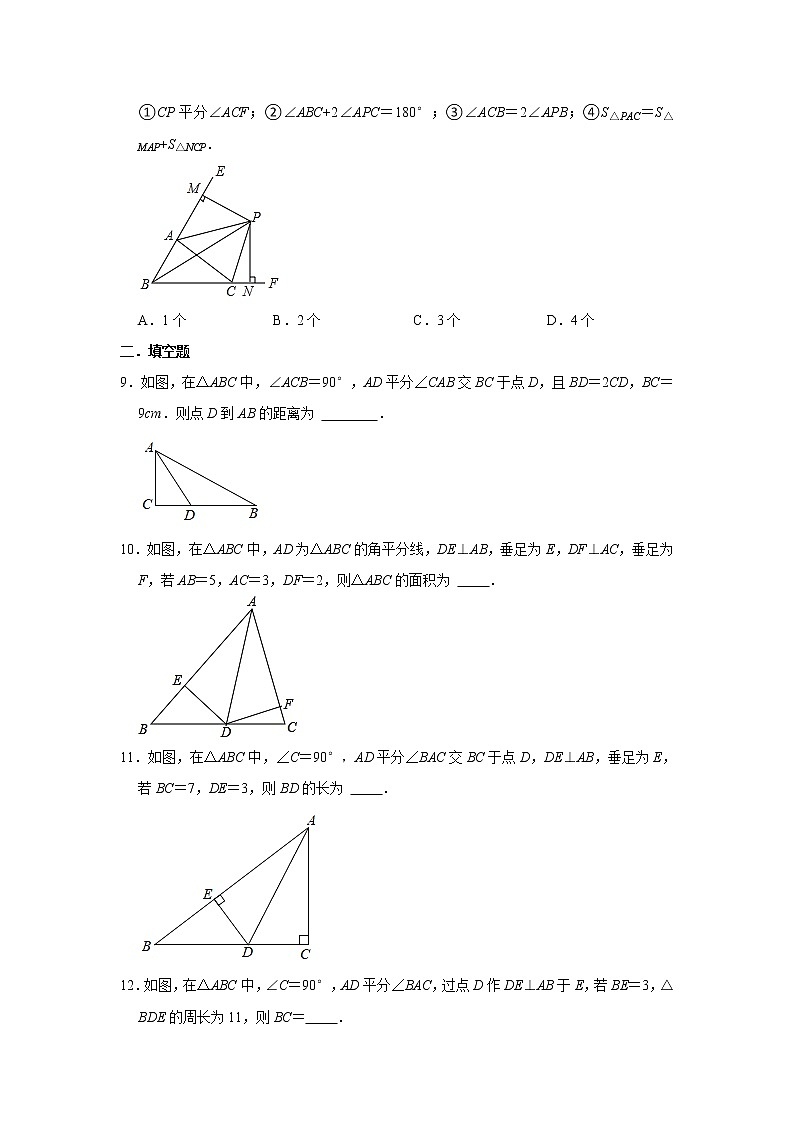
8．如图，△ABC中，∠ABC、∠EAC的角平分线BP、AP交于点P，延长BA、BC，PM⊥BE，PN⊥BF，则下列结论中正确的个数（　　）

①CP平分∠ACF；②∠ABC+2∠APC＝180°；③∠ACB＝2∠APB；④S△PAC＝S△MAP+S△NCP．

A．1个 B．2个 C．3个 D．4个

二．填空题

9．如图，在△ABC中，∠ACB＝90°，AD平分∠CAB交BC于点D，且BD＝2CD，BC＝9cm．则点D到AB的距离为 　    　．

10．如图，在△ABC中，AD为△ABC的角平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，若AB＝5，AC＝3，DF＝2，则△ABC的面积为 　 　．

11．如图，在△ABC中，∠C＝90°，AD平分∠BAC交BC于点D，DE⊥AB，垂足为E，若BC＝7，DE＝3，则BD的长为 　 　．

12．如图，在△ABC中，∠C＝90°，AD平分∠BAC，过点D作DE⊥AB于E，若BE＝3，△BDE的周长为11，则BC＝　 　．

13．如图所示，AD是△ABC的平分线，DF⊥AB于点F，DE＝DG，若S△DEF＝2，S△ADG＝9：则△ADE的面积为 　 　．

14．如图，△ABC的周长为20cm，若∠ABC，ACB的平分线交于点O，且点O到AC边的距离为cm，则△ABC的面积为 　   　cm2．

三．解答题

15．如图，在△ABC中，AD为∠BAC的平分线，DE⊥AB于E，DF⊥AC于F，△ABC的面积是64cm2，AB＝20cm，AC＝12cm，求DE的长．

16．点P为△ABC三内角平分线的交点，∠ACB＝90°，AB＝10cm，AC＝6cm，BC＝8cm，求：点P到三边的距离．

17．如图，在△ABC中，∠BAC＝90°，AB＝6，AC＝8，BC＝10，若AD平分∠BAC交BC于点D，求BD的长．

18．如图，已知△ABC的周长是20，BO和CO分别平分∠ABC和∠ACB，OD⊥BC于点D，OE⊥AB于点E，OF⊥AC于点F，且OD＝3，求△ABC的面积．

19．如图，BD平分∠ABC交AC于点D，DE⊥AB于E，DF⊥BC于F，AB＝6，BC＝8，若S△ABC＝28，求DE的长．

20．如图，DE⊥AB于E，DF⊥AC于F，若BD＝CD、BE＝CF．

（1）求证：AD平分∠BAC；

（2）直接写出AB+AC与AE之间的等量关系．

21．如图，在△ABC中，∠CAB＝60°，∠CAB的平分线AP与∠CBA的平分线BP相交于点P，连接CP．

（1）求证：CP平分∠ACB；

（2）若AP＝4，△ABC的周长为20，求△ABC的面积．

参考答案

一．选择题

1．解：如图，过点D作DE⊥AB于E，

∵∠C＝90°，AD平分∠BAC，

∴DE＝CD＝3，

∴△ABD的面积＝AB•DE＝×10×3＝15．

故选：A．

2．解：∵BD是∠ABC平分线，DE⊥AB，∠C＝90°，

∴DE＝CD＝2，

∵AC＝5，

∴AD＝AC﹣CD＝5﹣2＝3，

故选：B．

3．解：当DP⊥BC时，DP的值最小，

∵BD平分∠ABC，∠A＝90°

当DP⊥BC时，

DP＝AD，

∵AD＝3，

∴DP的最小值是3，

故选：A．

4．解：过O点作OD⊥AB，OE⊥BC，OF⊥AC，垂足分别为D，E，F，

∵△ABC的三条角平分线交于点O，

∴OD＝OE＝OF，

在Rt△ABC中，AB＝9，BC＝12，

∴AC＝，

∴S△ABO：S△BCO：S△CAO＝，

故选：C．

5．解：过D点作DH⊥AB于H，如图，

∵BD平分∠ABC，DC⊥BC，DH⊥BA，

∴DH＝DC＝4，

∴S四边形ABCD＝S△ABD+S△BCD＝×5×4+×9×4＝28．

故选：B．

6．解：根据垂线段最短可知：当PM⊥OC时，PM最小，

当PM⊥OC时，

又∵OP平分∠AOC，PD⊥OA，PD＝3，

∴PM＝PD＝3，

故选：B．

7．解：过O点作OE⊥AB于E，OF⊥AC于F，连接OA，如图，

∵点O为∠ABC与∠ACB的平分线的交点，

∴OE＝OF＝OD＝3，

∴四边形ABOC的面积＝S△ABO+S△ACO

＝•AB•OE+•AC•OF

＝×3×（AB+AC）

＝×3×18

＝27．

故选：A．

8．解：①过点P作PD⊥AC于D，

∵PB平分∠ABC，PA平分∠EAC，PM⊥BE，PN⊥BF，PD⊥AC，

∴PM＝PN，PM＝PD，

∴PM＝PN＝PD，

∴点P在∠ACF的角平分线上，故①正确；

②∵PM⊥AB，PN⊥BC，

∴∠ABC+90°+∠MPN+90°＝360°，

∴∠ABC+∠MPN＝180°，

在Rt△PAM和Rt△PAD中，

，

∴Rt△PAM≌Rt△PAD（HL），

∴∠APM＝∠APD，

同理：Rt△PCD≌Rt△PCN（HL），

∴∠CPD＝∠CPN，

∴∠MPN＝2∠APC，

∴∠ABC+2∠APC＝180°，②正确；

③∵PA平分∠CAE，BP平分∠ABC，

∴∠CAE＝∠ABC+∠ACB＝2∠PAM，∠PAM＝∠ABC+∠APB，

∴∠ACB＝2∠APB，③正确；

④由②可知Rt△PAM≌Rt△PAD（HL），Rt△PCD≌Rt△PCN（HL）

∴S△APD＝S△APM，S△CPD＝S△CPN，

∴S△APM+S△CPN＝S△APC，故④正确，

故选：D．

二．填空题

9．解：过D点作DE⊥AB于E，如图，

∵AD平分∠CAB，DC⊥AC，DE⊥AB，

∴DE＝DC，

∵BD＝2CD，BC＝9cm，

∴CD＝BC＝3cm，

∴DE＝3cm，

即点D到AB的距离为3cm．

故答案为3cm．

10．解：∵AD为△ABC的角平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，

∴DE＝DF＝2，

∵AB＝5，AC＝3，

∴S△ABC＝S△ABD+S△ACD

＝AB•DE+AC•DF

＝×5×2+×3×2

＝5+3

＝8．

故答案为：8．

11．解：∵AD平分∠BAC，DE⊥AB，∠C＝90°，

∴CD＝DE，

∵DE＝3，

∴CD＝3，

∴BD＝BC﹣CD＝7﹣3＝4．

故答案为：4．

12．解：∵△ABC中，∠C＝90°，

∴AC⊥CD，

∵AD平分∠BAC，DE⊥AB，

∴DE＝CD，

∵△BDE的周长为11，BE＝3，

∴△BDE的周长是：BE+BD+DE＝BE+BD+CD＝BE+BC＝3+BC＝11．

∴BC＝8，

故答案为：8．

13．解：过点D作DH⊥AC于H，

∵AD是△ABC的角平分线，DF⊥AB，DH⊥AC，

∴DH＝DF，

在Rt△DEF和Rt△DGH中，

，

∴Rt△DEF≌Rt△DGH（HL），

∴△DEF的面积＝△DGH的面积＝2，

同理可证，Rt△ADF≌Rt△ADH，

∴△ADF的面积＝△ADH的面积＝9﹣2＝7，

∴△ADE的面积＝△ADF的面积﹣△DEF的面积＝7﹣2＝5，

故答案为：5．

14．解：连接OA，过O作OE⊥AB于E，OG⊥AC于G，OF⊥BC于F，

∵∠ABC，ACB的平分线交于点O，

∴OE＝OF，OG＝OF，

∴OE＝OF＝OG，

∵点O到AC边的距离为cm，

∴OE＝OF＝OG＝cm，

∵△ABC的周长为20cm，

∴AB+BC+AC＝20cm，

∴△ABC的面积S＝S△ABO+S△BCO+S△ACO

＝

＝××（AB+BC+AC）

＝×20

＝15（cm2），

故答案为：15．

三．解答题

15．解：∵AD为∠BAC的平分线，DE⊥AB，DF⊥AC，

∴DE＝DF，

∵S△ABD+S△ACD＝S△ABC，

∴×20×DE+×12×DF＝64，

即10DE+6DE＝64，

∴DE＝4（cm）．

答：DE的长为4cm．

16．解：∵点P为三角形三个内角平分线的交点，作PD⊥BC于D，PE⊥AC于E，PF⊥AB于F，连接PA，PB，PC，如图，

∴PD＝PE＝PF，

设PD＝PE＝PF＝R，

由三角形的面积公式得：S△ACB＝S△APC+S△APB+S△BPC，

∴×AC×BC＝×AC×R+×BC×R+×AB×R，

6×8＝6R+8R+10R，

R＝2，

即PD＝2cm．

答：点P到三边的距离为2cm．

17．解：过A点作AH⊥BC于H，过D点作DE⊥AB于E，DF⊥AC于F，如图，

∵AH•BC＝AC•AB，

∴AH＝＝，

∵AD平分∠BAC，

∴DE＝DF，

∵AB•DE+AC•DF＝AB•AC，

∴3DE+4DF＝24，

∴DE＝，

∵S△ABD＝AH•BD＝AB•DE，

∴BD＝＝．

18．解：∵OB、OC分别平分∠ABC和∠ACB，OD⊥BC于点D，OE⊥AB于点E，OF⊥AC于点F，

∴OE＝OF＝OD，

∵OD＝3，

∴OE＝OF＝OD＝3，

∵△ABC的周长是20，

∴S△ABC＝×AB×OE+×BC×OD+×AC×OF＝×（AB+BC+AC）×3

＝×20×3＝30．

19．解：∵BD平分∠ABC交AC于点D，DE⊥AB，DF⊥BC，

∴DE＝DF，

∵AB＝6，BC＝8，S△ABC＝28，

∴S△ABC＝S△ABD+S△BCD＝AB•DE+BC•DF＝DE•（AB+BC）＝28，

即DE（6+8）＝28，

∴DE＝4．

20．（1）证明：∵DE⊥AB于E，DF⊥AC于F，

∴∠E＝∠DFC＝90°，

∴△BDE与△CDF均为直角三角形，

∵

∴△BDE≌△CDF（HL）．

∴DE＝DF，

∵DE⊥AB于E，DF⊥AC于F，

∴AD平分∠BAC；

（2）AB+AC＝2AE．

证明：∵BE＝CF，AD平分∠BAC，

∴∠EAD＝∠CAD，

∵∠E＝∠AFD＝90°，

∴∠ADE＝∠ADF．

在△AED与△AFD中，

∵，

∴△AED≌△AFD（ASA）．

∴AE＝AF．

∴AB+AC＝AE﹣BE+AF+CF＝AE+AE＝2AE．

21．（1）证明：过点P作PD⊥AB于D，作PE⊥BC于E，作PF⊥AC于F，

则PD，PE，PF分别是P到AB，BC，CA的距离，

∵AP平分∠CAB，BP平分∠ABC，

∴PD＝PF，PD＝PE，

∴PF＝PE，

∴CP平分∠ACB；

（2）解：∵∠CAB＝60°，

∴∠PAB＝30°，

在Rt△PAD中，PA＝4，

∴PD＝2，

∴S△ABC＝S△APB+S△BPC+S△CPA

＝AB•PD+BC•PE+CA•PF

＝（AB+BC+CA）•PD

＝×20×2

＝20．