人教版九年级上册第二十三章 旋转综合与测试精品课时练习

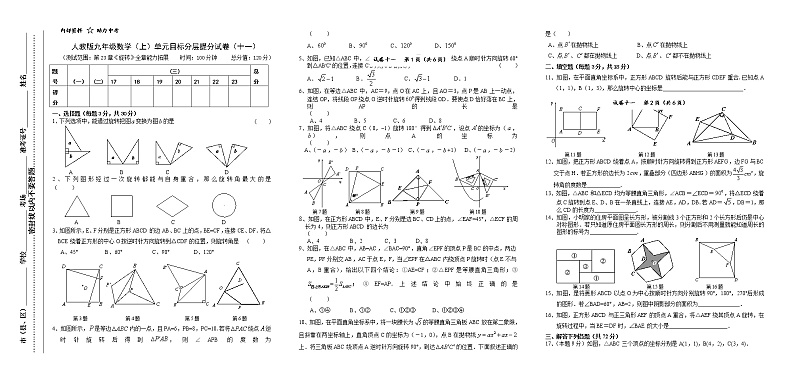
    人教版九年级数学（上）单元目标分层提分试卷（十一）

   （测试范围：第23章《旋转》全章能力拓展    时间：100分钟     总分值：120分）

一、选择题（每题3分，共30分）

1、下列选项中，能通过旋转把图变换为图的是                             ( 　　)

      A                 B               C                    D   

2、下列图形经过一次旋转都能与自身重合，那么旋转角最大的是              （     ）

    A              B                  C                 D

3、如图所示，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．将△BCE绕着正方形的中心O按逆时针方向旋转到△CDF的位置，则旋转角是  （　 　）

A、45°        B、60°        C、90°        D、120°

     第3题                第4题                   第5题              第6题

4、如图所示，是等边内的一点，且PA=6，PB=8，PC=10.若将绕点逆时针旋转后得到，则∠APB的度数为                             （     ）

   A、        B、        C、        D、

5、如图，已知△ABC中，∠C=90°，AC=BC=，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B，则C′B的长为                               （　 　）

A．        B．        C．        D．1

6、如图，在等边△ABC中，AC＝9，点O在AC上，且AO＝3，点P是AB上一动点，连结OP，将线段OP绕点O逆时针旋转得到线段OD．要使点D恰好落在BC上，则AP的长是                                                         （     ）

A、4       B、5       C、6        D、8

7、如图，将△ABC绕点C（0，1）旋转180°得到，设点的坐标为（，），则点A的坐标为                                                      （     ）

A、（－，－） B、（－，－－1） C、（－，－+1）  D、（－，－－2）

     第7题            第8题                 第9题                   第10题

8、如图，在正方形ABCD中，E、F分别是边BC、CD上的点，∠EAF=45°，△ECF的周长为4，则正方形ABCD的边长为                                       （     ）

A、4           B、2        C、3       D、8

9、如图，在△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC的中点，两边PE，PF分别交AB，AC于点E，F，当∠EPF在△ABC内绕顶点P旋转时（点E不与A，B重合），给出以下四个结论：①AE=CF；②△EPF是等腰直角三角形；③；④EF=AP.上述结论中始终正确的是                   （     ）

    A、①④       B、①②       C、①②③      D、①②③④

10、如图，在平面直角坐标系中，将一块腰长为的等腰直角三角板ABC放在第二象限，且斜靠在两坐标轴上，直角顶点C的坐标为（－1，0），点B在抛物线上．将三角板ABC绕顶点A逆时针方向旋转90°，到达的位置．下面叙述正确的是（    ）

A、点在抛物线上              B、点在抛物线上

 C、点、都在抛物线上       D、点、都不在抛物线上

二、填空题（每题3分，共18分）

11、如图，在平面直角坐标系中，正方形ABCD旋转后能与正方形CDEF重合.已知点A（1，1），B（1，3），那么旋转中心的坐标是_____________________________．

       第11题                        第12题                      第13题

12、如图，把正方形ABCD绕着点A，按顺时针方向旋转得到正方形AEFG，边FG与BC交于点H．若正方形的边长为2，重叠部分（四边形ABHG）的面积为，旋转角的度数是____________.

13、如图，△ABC和△ECD均为等腰直角三角形，∠ACB＝∠ECD＝，将△ECD绕着点C旋转到点E、D、B在一条直线上，连接AE，AD，DB.若AD＝，DB＝1，那么CD的长度为_______________.

14、如图，小明家的住房平面图呈长方形，被分割成3个正方形和2个长方形后仍是中心对称图形．若只知道原住房平面图长方形的周长，则分割后不用测量就能知道周长的图形的标号为_________________.

          第14题                        第15题                  第16题

15、如图，是将菱形ABCD以点O为中心按顺时针方向分别旋转90°，180°，270°后形成的图形．若∠BAD=60°，AB=2，则图中阴影部分的面积为_______________．

16、如图，正方形ABCD与正三角形AEF的顶点A重合，将△AEF绕其顶点A旋转，在旋转过程中，当BE＝DF时，∠BAE的大小是_____________________．

三、解答下列各题（共72分）

17、（本题9分）如图，△ABC三个顶点的坐标分别是A(1，1)，B(4，2)，C(3，4)．

(1)请画出△ABC向左平移5个单位

长度后得到的△A1B1C1；

(2)请画出△ABC关于原点对称的△A2B2C2；

(3)在轴上求作一点P，使△PAB周

长最小，请画出△PAB，并直接写出

点P的坐标．

18、（本题10分）如图所示，把正方形ABCD绕点C按顺时针方向旋转得到正方形 （此时，点落在对角线AC上，点落在CD的延长线上），交AD于点E，连接、CE．

求证：（1）≌；

     （2）直线CE是线段的垂直平分线．

19、（本题10分）（1）如图，正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，延长CD到点G，使DG=BE，连结EF，AG．求证：EF=FG．

（2）如图，等腰直角三角形ABC中，∠BAC=90°，AB=AC，点M，N在边BC上，且∠MAN=45°，若BM=1，CN=3，求MN的长．

       图1                       图2

20、（本题10分）如图1，点A是线段BC上一点，△ABD和△ACE都是等边三角形.
（1）连结BE，CD，求证：BE=CD；

（2）如图2，将△ABD绕点A顺时针旋转得到.
①当旋转角为_____________度时，边落在AE上；
②在①的条件下，延长交CE于点P，连接，.当线段AB，AC满足什么数量关系时，与全等？并给予证明.

                                       图1                           图2

21、（本题10分）【动手操作】：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点．如图①、②、③是旋转三角板得到的图形中的3种情况.

【解决问题】：

（1）三角板绕点P旋转，观察线段PD与PE之间有什么数量关系？并结合图②说明理由．

（2）三角板绕点P旋转，△PBE是否能成为等腰三角形？若能，直接写出CE的长；若不能，请说明理由．

          图①                          图②                             图③

22．（本题10分）如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．

（1）求证：AE=BC；

（2）如图2，过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角（0°＜＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；

（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．

     图1                         图2                           备用图

23、（本题12分）如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，

∠B=∠E=30°.

        图1                图2                                     图3

（1）操作发现

如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，

填空：①线段DE与AC的位置关系是_________；

②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是_________________.

（2）猜想论证

当△DEC绕点C旋转到图3所示的位置时，小明猜想（1）中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC、CE边上的高，请你证明小明的猜想.

（3）拓展探究

已知∠ABC=60°，点D是其角平分线上一点，

BD=CD=4，DE//AB交BC于点E（如图4）.

若在射线BA上存在点F，使S△DCF=S△BDE，

请直接写出相应的BF的长.