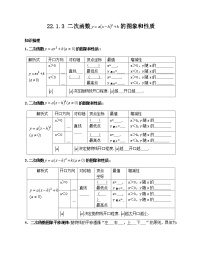
初中数学人教版九年级上册22.1.4 二次函数y＝ax2＋bx＋c的图象和性质第3课时导学案

这是一份初中数学人教版九年级上册22.1.4 二次函数y＝ax2＋bx＋c的图象和性质第3课时导学案，共5页。学案主要包含了知识点总结1等内容，欢迎下载使用。

y=ax2 、y=ax2+k 、 y=a(x-h)2
先完成下列表格(前三个函数):
【探究】 二次函数y=a(x-h)2+k的图象和性质
左下图为抛物线y=0.5x2 与 y=0.5(x+2)2 ，右下图为抛物线y=0.5x2 与 y=0.5x2-3，
在同一直角坐标系中,画出二次函数y=0.5(x+2)2-3的图象.
（思考：列表时，如何对横坐标取值可以使画出的图象比较美观？）

认真观察二次函数y=0.5(x+2)2-3的图象，并完成上面表格的最后一列和下列填空.
（1）二次函数 y=0.5(x+2)2-3的图象与二次函数y=0.5x2、 y=0.5x2-3、y=0.5(x+2)2的图象的
相同点是 、 ; 不同点是 、 .
（2）y=0.5(x+2)2-3的开口方向是 ，顶点坐标是 ，对称轴是 ，
当x= 时，y的最 值是 ，y=0.5(x+2)2-3不存在最 值；
（3）试用类比的方法写出下列形式的二次函数的最值和其图象的开口方向、顶点坐标、对称轴。
（4） ①抛物线y=0.5x2-3向 平移 个单位长度可以得到抛物线y=0.5(x+2)2-3
②抛物线y=0.5(x+2)2向 平移 个单位长度可以得到抛物线y=0.5(x+2)2-3
③抛物线y=0.5x2经过怎样的平移可以得到抛物线y=0.5(x+2)2-3 ？

(5)用类比的方法完成下列填空。
①抛物线y=-x2 可以得到抛物线y=-(x-2)2-6
②抛物线y=0.5x2 可以得到抛物线y=0.5(x-3)2+1
③抛物线y=0.2x2经过怎样的变换可以得到抛物线y=-0.2(x+1)2-3？
（6）对于函数y=0.5(x+2)2-3 的图象，
当 时，y随着x的增大而增大，图象从左到右呈 的趋势
当 时，y随着x的增大而减小，图象从左到右呈 的趋势
【知识点总结1】
抛物线y=a(x-h)2+k有如下特点:
(1)当a>0时,开口向上 ; 当a<0时,开口向下。
抛物线y=a(x-h)2+k的开口方向由a的正负决定
抛物线y=a(x-h)2+k的开口大小由 决定
(2)抛物线 y=a(x-h)2+k的对称轴是 .
(3)抛物线 y=a(x-h)2+k的顶点坐标是 . y=a(x-h)2+k 称为二次函数的 。
y=ax2+bx+c 称为二次函数的 。

(4)抛物线 y=a(x-h)2+k的增减性：
如果a > 0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
如果a < 0,当 时,y随x的增大而增大,当 时,y随x的增大而减小.
将抛物线y=ax2先向 或向 平移|k|个单位长度(k>0时,向 平移;k<0时,向 平移),
可得到抛物线y=ax2+k,
然后再将抛物线y=ax2+k向 或向 平移|h|个单位长度
(h>0时,向 平移;h<0时,向左平移),就可以得到抛物线y=a(x-h)2+k,
当然也可以先左、右移，再上、下移.
（6）二次函数y=a(x-h)2+k的最值：
当a>0时,y不存在最 值，y有最 值；当x= 时，
当a<0时,y不存在最 值，y有最 值；当x= 时，
(7)对于二次函数y=a(x-h)2+k，x的取值范围是 ；当a>0时，y的取值范围是：
当a<0时，y的取值范围是：

(8)对于二次函数y=a(x-h)2+k
①当a>0时,它的图象有最 点，y有最 值，y不存在最 值；
在对称轴的左侧，抛物线呈现 的趋势，y随x的增大而 ；
在对称轴的右侧，抛物线呈现 的趋势，y随x的增大而 ；
②当a<0时,它的图象有最 点，y有最 值，y不存在最 值；
在对称轴的左侧，抛物线呈现 的趋势，y随x的增大而 ；
在对称轴的右侧，抛物线呈现 的趋势，y随x的增大而 ；
y=0.5x2
y=0.5x2-3
y=0.5(x+2)2
y=0.5(x+2)2-3
开口方向
对称轴
顶点坐标
最值
增减性
函数解析式
开口方向
顶点坐标
对称轴
最值
y=-3(x-1)2-4
y=2(x-1)2-4
y= (x+1)2-5
y=-(x-1)2+2