北师大版必修42.2向量的减法说课课件ppt

这是一份北师大版必修42.2向量的减法说课课件ppt，共24页。PPT课件主要包含了怎样用向量来表示呢，长度相等方向相反，探究点向量减法，向量减法法则，1起点相同，1画出向量，练一练，2填空，例2化简，-OB-M0等内容，欢迎下载使用。
上周日杨恒从家骑车到八里河公园游玩, 然后再由八里河公园返回家中,我们把八里河公园记作B点,杨恒家记作A点,那么杨恒的位移是多少?
2.类比相反数的概念,我们如何定义上述两个向　　　　　　　　　量的关系?
与 长度相等、方向相反的向量，叫作　的相反向量.
３．类比相反数的性质,说明相反向量有哪些性质?
求两个向量差的运算，叫作向量的减法.
1.了解相反向量的概念.2.掌握向量的减法，会求两个向量的差.（重点）3.掌握向量减法的运算，并理解其几何意义.（难点）
如图，作 以OA,OB为边作平行四边形OACB，连接BA.
不难看出，向量 表示向量 与 　的和，也就是向量
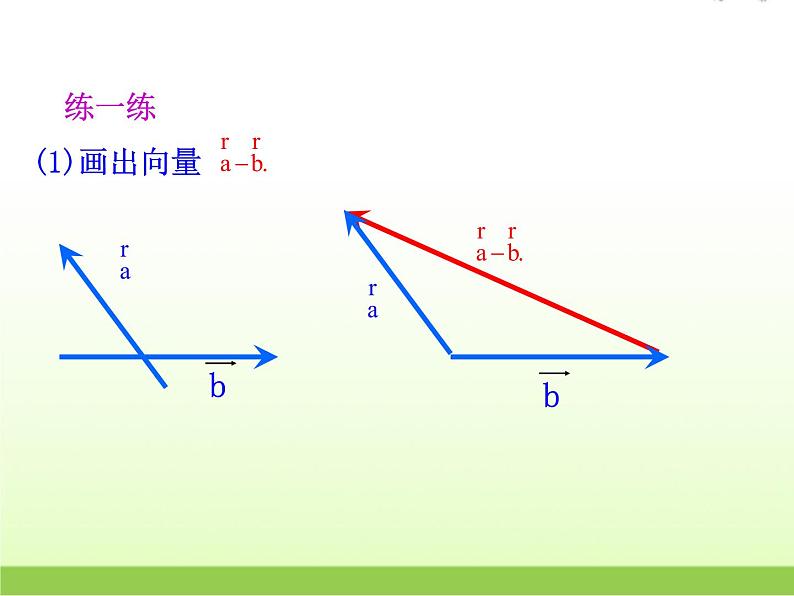
已知向量 如何作
两个向量起点相同，则两个向量的差就是连接两向量终点，指向被减向量终点的向量.
(2)由减向量的终点指向被减向量的终点.
(3)向量的差仍是向量.
同起点，连终点，指向被减.
(3)如图， 求作
以 为邻边的四边形是矩形
1.化简 的结果等于( )A. B. C. D.2.化简 为( )A. B. C. D.
4、如图，已知一点O 到平行四边形ABCD的三个顶点A，B，C的向量分别为 试用向量 表示 .
1.向量的减法的定义.
3. 可以表示为从向量 的终点指向向量 的终点的向量
２.向量减法可以看作一个向量加上 另一个向量的相反向量.
P80 练习 1、2习题2----2 A组 4、5