高中数学北师大版必修45从力做的功到向量的数量积课前预习ppt课件

这是一份高中数学北师大版必修45从力做的功到向量的数量积课前预习ppt课件，共21页。PPT课件主要包含了复习回顾，知识梳理，非零向量，类型二求向量的模，类型三求向量的夹角等内容，欢迎下载使用。
1.了解平面向量数量积的物理背景，即物体在力F的作用下产生位移s所做的功.2.掌握平面向量数量积的定义和运算律，理解其几何意义.3.会用两个向量的数量积求两个向量的夹角以及判断两个向量是否垂直．
知识点一　两向量的夹角
思考1　平面中的任意两个向量都可以平移至同一起点，它们存在夹角吗？若存在，向量的夹角与直线的夹角一样吗？
知识点二 平面向量数量积的物理背景及其定义
一个物体在力F的作用下产生位移s，如图．
思考1　如何计算这个力所做的功？
思考2　力做功的大小与哪些量有关？
W＝|F||s|cs θ
与力的大小、位移的大小及它们之间的夹角有关
(1)数量积：已知两个非零向量a与b，它们的夹角为θ，我们把______________叫作a与b的数量积(或内积)，记作a·b，即a·b＝____________.(2)数量积的特殊情况当两个向量相等时，a·a＝__________.当两个向量e1，e2是单位向量时，e1·e2＝______________.
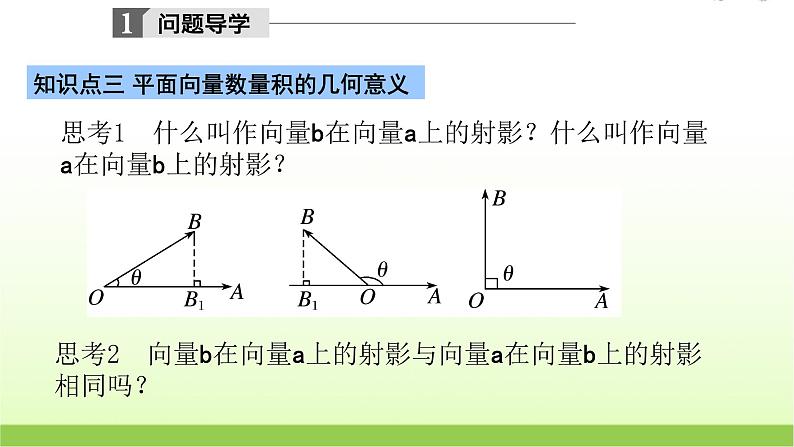
知识点三 平面向量数量积的几何意义
思考1　什么叫作向量b在向量a上的射影？什么叫作向量a在向量b上的射影？
思考2　向量b在向量a上的射影与向量a在向量b上的射影相同吗？
(1)射影：若非零向量a，b的夹角为θ，则________叫作向量b在a方向上的射影(简称为投影)．(2)a·b的几何意义：a与b的数量积等于a的长度|a|与b在a方向上的射影________的乘积，或b的长度|b|与a在b方向上的射影____________的乘积．
知识点四 平面向量数量积的性质
思考1　向量的数量积运算的结果和向量的线性运算的结果有什么区别？
思考2　非零向量的数量积是否可为正数，负数和零，其数量积的符号由什么来决定？
由两个非零向量的夹角决定．当0°≤θ＜90°时，非零向量的数量积为正数．当θ＝90°时，非零向量的数量积为零．当90°＜θ≤180°时，非零向量的数量积为负数．
向量的线性运算的结果是向量，而向量的数量积运算的结果是数量．
类型一　求两向量的数量积
例1　已知|a|＝4，|b|＝5，当(1)a∥b；(2)a⊥b；(3)a与b的夹角为30°时，分别求a与b的数量积．
反思与感悟　求平面向量数量积的步骤：(1)求a与b的夹角θ，θ∈[0°，180°]；(2)分别求|a|和|b|；(3)求数量积，即a·b＝|a||b|cs θ，要特别注意书写时a与b之间用实心圆点“·”连接，而不能用“×”连接，也不能省去．
引申探究若本例中条件不变，求|2a＋b|，|a－2b|.
跟踪训练2　已知|a|＝|b|＝5，且|3a－2b|＝5，求|3a＋b|的值．
例3　设n和m是两个单位向量，其夹角是60°，求向量a＝2m＋n与b＝2n－3m的夹角．
反思与感悟　当求向量夹角时，应先根据公式把涉及到的量先计算出来再代入公式求角，注意向量夹角的范围是[0，π]．
跟踪训练3　已知a·b＝－9，a在b方向上的射影为－3，b在a方向上的射影为－ ，求a与b的夹角θ.
1．已知|a|＝8，|b|＝4，〈a，b〉＝120°，则向量b在a方向上的射影为(　　)A．4 B．－4 C．2 D．－22．设向量a，b满足|a＋b|＝ ，|a－b|＝ 则a·b等于(　　)A．1 B．2 C．3 D．53．若a⊥b，c与a及与b的夹角均为60°，|a|＝1，|b|＝2，|c|＝3，则(a＋2b－c)2＝________.