北师大版必修47.2向量的应用举例评课ppt课件

这是一份北师大版必修47.2向量的应用举例评课ppt课件，共21页。PPT课件主要包含了x0y0，点到直线的距离，点到直线的距离公式，特别提醒，x0y1，x1y0，思路分析，由形到向量，向量的运算，向量和数到形等内容，欢迎下载使用。
平行、垂直、夹角、距离、全等、相似等，是平面几何中常见的问题，而这些问题都可以由向量的线性运算及数量积表示出来.因此，平面几何中的某些问题可以用向量方法来解决，但解决问题的数学思想、方法和技能，需要我们在实践中去探究、领会和总结.
1.了解直线法向量的概念.2.掌握利用向量方法解决平面几何问题，体会解析法和向量方法的区别与联系.(重点)3.会用向量方法解决物理问题，会用所学知识解决实际问题.（难点）
思考1 用向量方法解决平面几何问题的基本思路是什么？
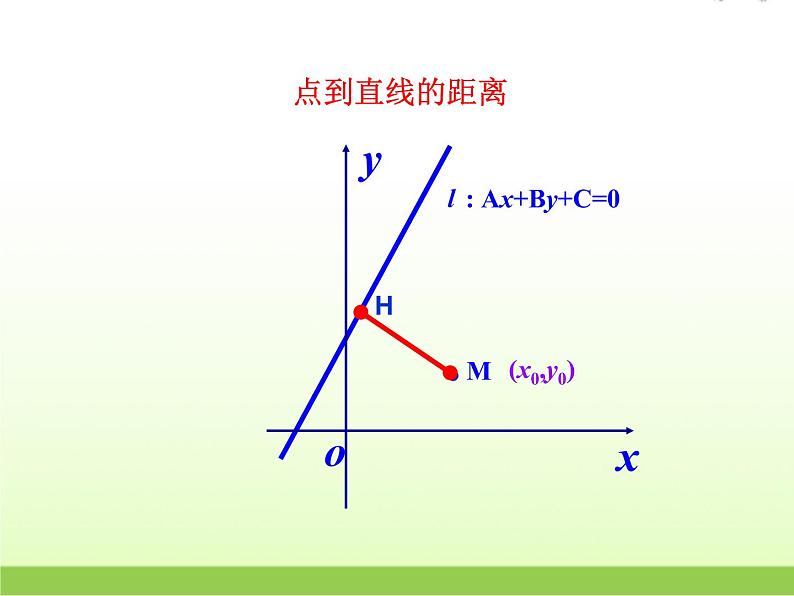
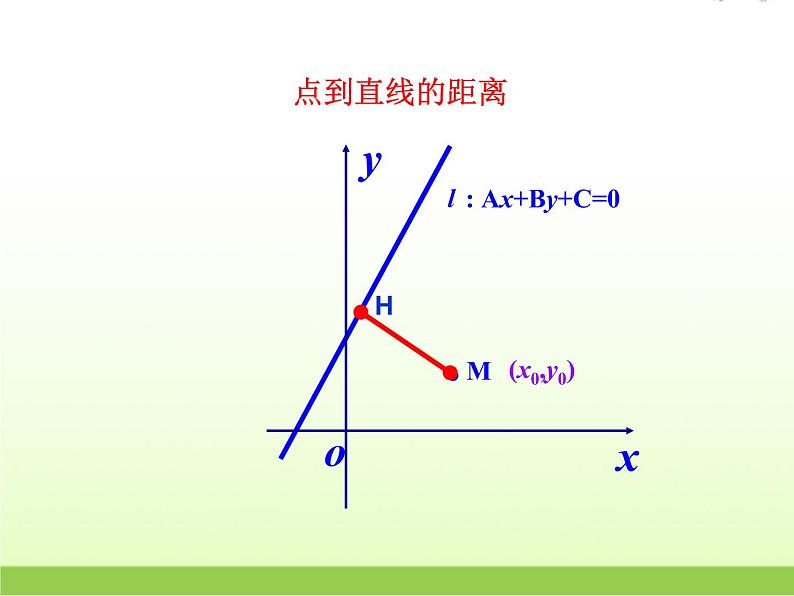
探究点1 点到直线的距离公式
: Ax+By+C=0
已知点M(x0, y0)和直线l:Ax+By+C=0.
则点M到直线 l 的距离d为:
思考2 如何借助向量的方法来证明点到直线的距离公式？
l: Ax+By+C=0
1.在使用该公式前，需将直线方程化为一般式．2. A=0或B=0，此公式也成立，但当A=0且B=0时一般不用此公式计算距离．
当A=0或B=0时,直线方程为y=y1或x=x1的形式.
探究点2 几何中的应用举例（三线共点问题）例2 如图,已知AD，BE，CF分别是△ABC的三条高， 求证：AD，BE，CF相交于同一点.
解决此类问题一般是将相关的线段用向量表示，利用向量的三角形法则和平行四边形法则，结合题目中的已知条件进行运算，得出结果，再翻译成几何语言 .
1.建立平面几何与向量的联系，用向量表示问题中涉及的几何元素，将平面几何问题转化为向量问题.2.通过向量运算，研究几何元素之间的关系，如距离、夹角等问题.3.把运算结果“翻译”成几何元素.
思考3 根据例题你能总结一下利用向量法解决平面几何问题的基本思路吗？
用向量方法解决平面几何问题的“三步曲”：
1.证明直径所对的圆周角是直角.
如图所示，已知⊙O，AB为直径，C为⊙O上任意一点，不与AB重合.求证∠ACB=90°.
证明：设 则 ，由此可得：
即 ， ∠ACB=90°.
注意:用该公式时应先将直线方程化为一般式.
1.点到直线的距离公式： ，
2.掌握用向量方法解决平面几何问题的三个步骤：