






高考数学一轮复习第十篇计数原理、概率、随机变量及其分布第6节离散型随机变量的分布列及均值和方差课件理
展开第6节 离散型随机变量的分布列及均值和方差
知识梳理自测 把散落的知识连起来
1.随机变量和函数有何联系和区别?提示:联系:随机变量和函数都是一种映射,随机变量是随机试验结果到实数的映射,函数是实数到实数的映射,随机试验结果的范围相当于函数的定义域,随机变量的取值范围相当于函数的值域.区别:随机变量的自变量是试验结果,而函数的自变量是实数.2.离散型随机变量分布列的性质是什么? 提示:随机变量的各个值对应的概率在[0,1]上且取所有值的概率之和等于1.3.离散型随机变量方差的意义是什么?提示:随机变量的取值与其均值的偏离程度,方差越大偏离程度越大.
1.离散型随机变量的概念与分布列(1)随机变量:一般地,如果随机试验的结果,可以用一个变量来表示,那么这样的变量叫做随机变量.通常用大写字母X,Y,Z(或小写希腊字母ξ,η,ζ)等表示,而用小写字母x,y,z(加上适当下标)等表示随机变量取的可能值.所有取值可以一一列出的随机变量,称为 .
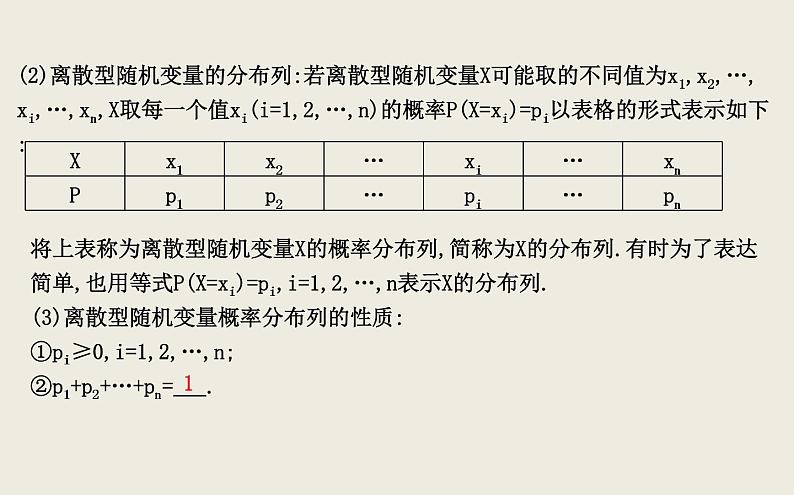
(2)离散型随机变量的分布列:若离散型随机变量X可能取的不同值为x1,x2,…,xi,…,xn,X取每一个值xi(i=1,2,…,n)的概率P(X=xi)=pi以表格的形式表示如下:
将上表称为离散型随机变量X的概率分布列,简称为X的分布列.有时为了表达简单,也用等式P(X=xi)=pi,i=1,2,…,n表示X的分布列.(3)离散型随机变量概率分布列的性质:①pi≥0,i=1,2,…,n;②p1+p2+…+pn= .
2.离散型随机变量的均值(1)概念:一般地,若离散型随机变量X的分布列为
则称E(X)= 为随机变量X的均值或数学期望.它反映了离散型随机变量取值的平均水平.(2)性质:若Y=aX+b,其中X是随机变量,a,b是常数,随机变量X的数学期望是E(X),则E(Y)= .
x1p1+x2p2+…+xipi+…+xnpn
3.离散型随机变量的方差(1)概念:离散型随机变量X的分布列为
则(xi-E(X))2描述了xi(i=1,2,3,…,n)相对于均值E(X)的偏离程度.而D(X)= ,为这些偏离程度的加权平均,刻画了随机变量X与其均值E(X)的平均偏离程度.我们称D(X)为随机变量X的方差,称其算术平方根 为随机变量X的标准差.
(2)性质:D(aX+b)=a2D(X).
4.两点分布和超几何分布(1)两点分布的分布列、均值和方差
若X服从成功概率为p的两点分布,则均值E(X)=p,方差D(X)=p(1-p).
(2)超几何分布概念与分布列其基本模型为“在含有M件次品的N件产品中,任取n件,其中恰有X件次品数,则事件{X=k}发生的概率为P(X=k)= ,k=0,1,2,…,m,其中m=min{M,n},且n≤N,M≤N,n,M,N∈N*”称分布列
为超几何分布列,如果随机变量X的分布列为超几何分布列,则称随机变量X服从超几何分布.
1.抛掷甲、乙两颗骰子,所得点数之和为X,那么X=4表示的基本事件是( )(A)一颗是3点,一颗是1点(B)两颗都是2点(C)一颗是3点,一颗是1点或两颗都是2点(D)甲是3点,乙是1点或甲是1点,乙是3点或两颗都是2点
解析:甲是3点,乙是1点与甲是1点,乙是3点是试验的两个不同结果,故选D.
2.某射手射击所得环数X的分布列为则此射手“射击一次命中环数大于7”的概率为( )(A)0.28(B)0.88(C)0.79(D)0.51
解析:P(X>7)=P(X=8)+P(X=9)+P(X=10)=0.28+0.29+0.22=0.79.
3.投掷一枚硬币,规定正面向上得1分,反面向上得-1分,则X的期望E(X)= .
解析:X的分布列为所求的均值为E(X)=-1×0.5+1×0.5=0.答案:0
4.一盒中有12个乒乓球,其中9个新的,3个旧的,从盒子中任取3个球来用,用完即为旧的,用完后装回盒中,此时盒中旧球个数X是一个随机变量,则P(X=4)的值为 .
考点专项突破 在讲练中理解知识
离散型随机变量的分布列
【例1】 导学号 38486211 为推动乒乓球运动的发展,某乒乓球比赛允许不同协会的运动员组队参加.现有来自甲协会的运动员3名,其中种子选手2名;乙协会的运动员5名,其中种子选手3名.从这8名运动员中随机选择4人参加比赛.
(1)设A为事件“选出的4人中恰有2 名种子选手,且这2名种子选手来自同一个协会”,求事件A发生的概率;
(2)设X为选出的4人中种子选手的人数,求随机变量X的分布列.
跟踪训练1:从集合{1,2,3,4,5}的所有非空子集中,等可能地取出一个,记所取出的非空子集的元素个数为ξ,求ξ的分布列.
离散型随机变量的均值★★★★
考查角度1:求离散型随机变量的均值【例2】 导学号 38486212 (2017·山东德州一模)某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学(成绩得分为整数,满分100分)进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4∶2∶1,落在[80,90)的人数为12人.
(2)按规定预赛成绩不低于90分的选手参加决赛,已知甲、乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.①甲不排在第一位乙不排在最后一位的概率;②记甲、乙二人排在前三位的人数为X,求X的分布列和数学期望.
反思归纳 求离散型随机变量均值的步骤:(1)理解随机变量X的意义,写出X可能取得的全部值;(2)求X的每个值的概率;(3)写出X的分布列;(4)由均值定义求出E(X).
【例3】 导学号 38486213 (2016·武汉市武昌区高三调研)某城市随机抽取一年内100天的空气质量指数(AQI)的监测数据,结果统计如下:
(1)若本次抽取的样本数据有30 天是在供暖季,其中有8 天为严重污染.根据提供的统计数据,完成下面的2×2 列联表,并判断是否有95%的把握认为“该城市本年的空气严重污染与供暖有关”?
反思归纳 求解离散型随机变量的分布列与数学期望时,一定要明确每个变量的取值所对应的事件发生的过程,这样才能判断事件的性质,进而选用相应的概率模型求其概率.
【例4】 导学号 18702589 如图,A,B两点由5条连线并联,它们在单位时间内能通过信息的最大量依次为2,3,4,3,2,现将从中任取三条线且在单位时间内都通过最大信息量的总量记为X.求X的均值和方差.
反思归纳 计算离散型随机变量的方差关键是先求分布列,只要知道了分布列,就可以求出均值进而根据公式求出方差.
超几何分布及其应用★★★★
考查角度1:利用超几何分布模型求概率【例5】 导学号 18702591 在15个村庄中有7个村庄交通不方便,现从中任意选10个村庄,用ξ表示这10个村庄中交通不方便的村庄数,下列概率等于 的是( )(A)P(ξ=2) (B)P(ξ≤2) (C)P(ξ=4)(D)P(ξ≤4)
考查角度2:求超几何分布的均值【例6】 导学号 38486214 (2017·山东卷)在心理学研究中,常采用对比试验的方法评价不同心理暗示对人的影响,具体方法如下:将参加试验的志愿者随机分成两组,一组接受甲种心理暗示,另一组接受乙种心理暗示,通过对比这两组志愿者接受心理暗示后的结果来评价两种心理暗示的作用,现有6名男志愿者A1,A2,A3,A4,A5,A6和4名女志愿者B1,B2,B3,B4,从中随机抽取5人接受甲种心理暗示,另5人接受乙种心理暗示.
(1)求接受甲种心理暗示的志愿者中包含A1但不包含B1的概率;
(2)用X表示接受乙种心理暗示的女志愿者人数,求X的分布列与数学期望EX.
反思归纳 超几何分布是非常重要的一个概率分布,它具有极为广泛的应用,其基本特点是总体有A,B两类元素(如男女、正品次品等)组成,从总体中不放回地取出一定数目的元素,其中含有一类元素的个数即服从超几何分布.超几何分布中随机变量取各个值的概率是古典概型,使用古典概型的公式进行计算.
【例1】 (2017·北京卷)为了研究一种新药的疗效,选100名患者随机分成两组,每组各50名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标x和y的数据,并制成下图,其中“*”表示服药者,“+”表示未服药者.
(1)从服药的50名患者中随机选出一人,求此人指标y的值小于60的概率;
(2)从图中A,B,C,D四人中随机选出两人,记ξ为选出的两人中指标x的值大于1.7的人数,求ξ的分布列和数学期望E(ξ);
(3)试判断这100名患者中服药者指标y数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
【例2】 (2017·山东泰安一模)在学校组织的“环保知识”竞赛活动中,甲、乙两班各6名参赛选手的成绩的茎叶图都受到了污损,如图.
(1)求乙班总分超过甲班的概率;
(2)若甲班污损的学生成绩是90分,乙班污损的学生成绩为97分,现从甲、乙两班所有选手成绩中各随机抽取2个,记抽取到成绩高于90分的选手的总人数为ξ,求ξ的分布列及数学期望.
解题规范夯实 把典型问题的解决程序化
求解概率综合题的解题步骤【典例】 (12分)(2017·全国Ⅲ卷)某超市计划按月订购一种酸奶,每天进货量相同,进货成本每瓶4元,售价每瓶6元,未售出的酸奶降价处理,以每瓶2元的价格当天全部处理完.根据往年销售经验,每天需求量与当天最高气温(单位:℃)有关.如果最高气温不低于25,需求量为500瓶;如果最高气温位于区间[20,25),需求量为300瓶;如果最高气温低于20,需求量为200瓶.为了确定六月份的订购计划,统计了前三年六月份各天的最高气温数据,得下面的频数分布表:
以最高气温位于各区间的频率代替最高气温位于该区间的概率.(1)求六月份这种酸奶一天的需求量X(单位:瓶)的分布列;(2)设六月份一天销售这种酸奶的利润为Y(单位:元),当六月份这种酸奶一天的进货量n(单位:瓶)为多少时,Y的数学期望达到最大值?
………………………………………………………………………5分
(2)由题意知,这种酸奶一天的需求量至多为500,至少为200,因此只需考虑200≤n≤500.当300≤n≤500时,若最高气温不低于25,则Y=6n-4n=2n,若最高气温位于区间[20,25),则Y=6×300+2(n-300)-4n=1 200-2n,若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,因此E(Y)=2n×0.4+(1 200-2n)×0.4+(800-2n)×0.2=640-0.4n, ……………………………………………………………………………8分
当200≤n<300时,若最高气温不低于20,则Y=6n-4n=2n,若最高气温低于20,则Y=6×200+2(n-200)-4n=800-2n,因此E(Y)=2n×(0.4+0.4)+(800-2n)×0.2=160+1.2n. ………………11分所以n=300时,Y的数学期望达到最大值,最大值为520元. ……………12分
答题模板第一步:确定需求量X的可能取值及相应的概率;第二步:写出X的分布列;第三步:根据最高气温的变化,写出利润Y的表达式;第四步:写出E(Y);第五步:确定E(Y)最大时的n.
备战2024高考一轮复习数学(理) 第十一章 计数原理与概率、随机变量及其分布 第五节 离散型随机变量的分布列及均值、方差课件PPT: 这是一份备战2024高考一轮复习数学(理) 第十一章 计数原理与概率、随机变量及其分布 第五节 离散型随机变量的分布列及均值、方差课件PPT,共49页。PPT课件主要包含了X服从两点分布,PX=1,数学期望,平均水平,平均偏离程度,标准差,aEX+b,a2DX,答案B,答案D等内容,欢迎下载使用。
高中数学高考2018高考数学(理)大一轮复习课件:第十一章 计数原理、概率、随机变量及其分布列 第五节 离散型随机变量的分布列、均值与方差: 这是一份高中数学高考2018高考数学(理)大一轮复习课件:第十一章 计数原理、概率、随机变量及其分布列 第五节 离散型随机变量的分布列、均值与方差,共55页。
高考数学(理数)一轮复习课件:第十一章 计数原理、概率、随机变量及其分布列 第五节 离散型随机变量的分布列、均值与方差 (含详解): 这是一份高考数学(理数)一轮复习课件:第十一章 计数原理、概率、随机变量及其分布列 第五节 离散型随机变量的分布列、均值与方差 (含详解),共55页。












