高考数学一轮复习第一章集合与常用逻辑用语1.4简单的逻辑联结词、全称量词与存在量词课件文

这是一份高考数学一轮复习第一章集合与常用逻辑用语1.4简单的逻辑联结词、全称量词与存在量词课件文，共33页。PPT课件主要包含了-2-，知识梳理，双基自测，“且”“或”“非”，-3-，-4-，∀x∈Mpx，-5-，-6-，-7-等内容，欢迎下载使用。
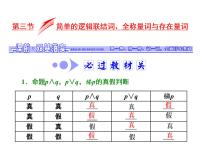
1.简单的逻辑联结词(1)命题中的　　　　　　　　　　　叫做逻辑联结词. (2)命题p∧q,p∨q, p的真假判断
2.全称量词和存在量词
3.全称命题和特称命题
∃x0∈M,p(x0)
4.含有一个量词的命题的否定
∃x0∈M,¬p(x0)
　∀x∈M,¬p(x)
1.下列结论正确的打“√”,错误的打“×”.(1)若命题p∧q为假命题,则命题p,q都是假命题. (　　)(2)命题“4>6或3>2”是真命题. (　　)(3)若p∧q为真,则p∨q必为真;反之,若p∨q为真,则p∧q必为真. (　　)(4)(教材习题改编P26T1(4))“梯形的对角线相等”是特称命题. (　　)(5)命题“菱形的对角线相等”的否定是“菱形的对角线不相等”. (　　)
2.已知命题p:∀x>0,lg2x0,lg2x≥2x+3B.∃x0>0,lg2x0≥2x0+3C.∃x0>0,lg2x00;命题q:若a>b,则a2>b2,下列命题为真命题的是(　　)A.p∧qB.p∧(?q)C.(?p)∧qD.(?p)∧(?q)思考如何判断含简单逻辑联结词的命题的真假?
解题心得要判断一个含有逻辑联结词的命题的真假,首先判断构成这个命题的每个简单命题的真假,然后依据“p∨q见真即真”“p∧q见假即假”“p与¬p真假相反”做出判断.
(2)已知命题p:对任意x∈R,总有2x>0;命题q:“x>1”是“x>2”的充分不必要条件,则下列命题为真命题的是(　　)A.p∧qB.(?p)∧(?q)C.(?p)∧qD.p∧(?q)
对点训练1(1)已知命题p:函数f(x)=|cs x|的最小正周期为2π;命题q:函数y=x3+sin x的图象关于原点中心对称,则下列命题是真命题的是(　　)A.p∧qB.p∨qC.(?p)∧(?q)D.p∨(?q)
例2(1)下列命题中,为真命题的是(　　) B.任意x∈(0,π),sin x>cs xC.任意x∈(0,+∞),x2+1>xD.存在x0∈R, +x0=-1(2)设非空集合A,B满足A⊆B,则以下表述正确的是(　　)A.∃x0∈A,x0∈BB.∀x∈A,x∈BC.∃x0∈B,x0∈AD.∀x∈B,x∈A思考如何判断一个全称命题是真命题?又如何判断一个特称命题是真命题?
解题心得1.判定全称命题“∀x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判断特称命题是真命题,只要在限定集合内至少能找到一个x0,使p(x0)成立.2.不管是全称命题,还是特称命题,若其真假不容易正面判断时,可先判断其否定的真假.
对点训练2下列命题中,为真命题的是(　　)A.∀x∈R,x2>0B.∀x∈R,-1