2021年安徽省淮南市八年级上学期数学期中试卷

这是一份2021年安徽省淮南市八年级上学期数学期中试卷，共11页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1.下列四个地铁标志中，是轴对称图形的是（ ）
A. B. C. D.
2.以下各组线段为边，能组成三角形的是( )
A. 1cm，2cm，3cm B. 1cm，3cm，5cm， C. 2cm，3cm，4cm D. 2cm，4cm，6cm
3.在平面直角坐标系中，点A关于x轴的对称点为A1(3，-2)，则点A的坐标为( )
A. (3，2) B. (-3，-2) C. (3，-2) D. (-3、7)
4.一个多边形的每一个外角都等于 ，则这个多边形的边数 等于（ ）
A. 8 B. 10 C. 12 D. 14
5.在三角形的内部，有一个点到三角形三个顶点的距离相等，则这个点一定是三角形（ ）
A. 三条中线的交点 B. 三条角平分线的交点 C. 三条边的垂直平分线的交点 D. 三条高的交点
6.如图，已知 的3条边和3个角，则能判断和 全等的是（ ）
A. 甲和乙 B. 乙和丙 C. 只有乙 D. 只有丙
7.如图， 是 的外角 的平分线， ，则 的度数是（ ）
A. 64° B. 40° C. 30° D. 32°
8.如图， 中， ， ，BD、CD分别平分∠ABC ， ∠ACB ， 过点D作直线平行于BC ， 分别交AB、AC于E、F ， 则 的周长为 ( )
A. 12 B. 13 C. 14 D. 15
9.如图，已知 ， ， 于点C， 于点G，若 ，则 长度是（ ）
A. 3 B. 4 C. 5 D. 6
10.如图， 中， ， ， ， ,将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F ， 则线段EF的长为（ ）
A. B. C. 4 D.
二、填空题
11.七边形的内角和是
12.等腰三角形的两边长分别是3和7，则其周长为________．
13.如图,在 中, , , 于点A,若 ,则BD=________.
14.如图，在△ABC中，∠A =65°，∠B =45°, BC的垂直平分线分别交AB、BC于D、E，则∠ACD=________°.
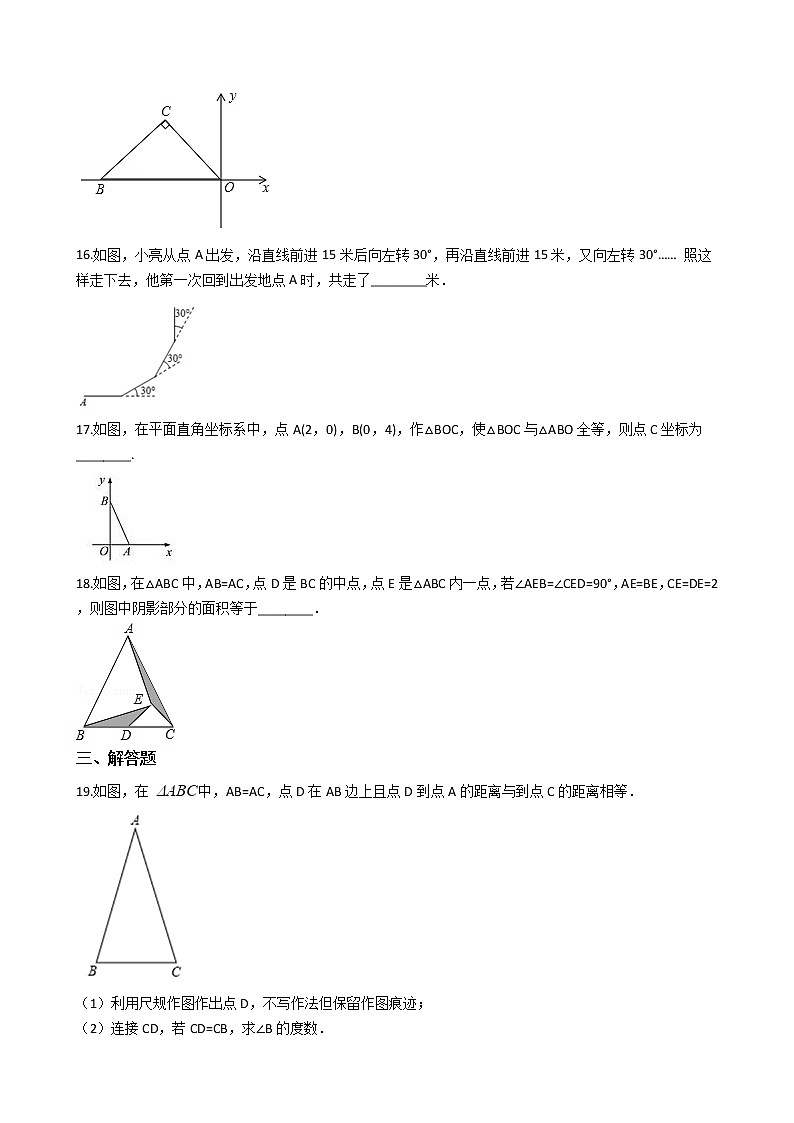
15.如图，在直角坐标系中，△OBC的顶点O（0，0），B（﹣6，0），且∠OCB＝90°，OC＝BC，则点C关于y轴对称的点的坐标是 ________．
16.如图，小亮从点A出发，沿直线前进15米后向左转30°，再沿直线前进15米，又向左转30°…… 照这样走下去，他第一次回到出发地点A时，共走了________米．
17.如图，在平面直角坐标系中，点A(2，0)，B(0，4)，作△BOC，使△BOC与△ABO全等，则点C坐标为________.

18.如图，在△ABC中，AB=AC，点D是BC的中点，点E是△ABC内一点，若∠AEB=∠CED=90°，AE=BE，CE=DE=2，则图中阴影部分的面积等于________．
三、解答题
19.如图，在 中，AB=AC，点D在AB边上且点D到点A的距离与到点C的距离相等．
（1）利用尺规作图作出点D，不写作法但保留作图痕迹；
（2）连接CD，若CD=CB，求∠B的度数．
20.如图， 和 均为等腰直角三角形， ，点A ， D ， E在同一直线上，CM为 中DE边上的高，连接BE.
（1）求 的度数.
（2）试证明 .
答案解析部分
一、单选题
1.【答案】 B
【解析】【解答】解：A、不是轴对称图形，不合题意；
B、是轴对称图形，符合题意；
C、不是轴对称图形，不合题意；
D、不是轴对称图形，不合题意.
故答案为：B.
【分析】直接利用轴对称图形的定义得出答案.
2.【答案】 C
【解析】【解答】解：A、 ，不满足三角形的三边关系定理，则不能组成三角形，此项不符题意；
B、 ，不满足三角形的三边关系定理，则不能组成三角形，此项不符题意；
C、 ，满足三角形的三边关系定理，则能组成三角形，此项符合题意；
D、 ，不满足三角形的三边关系定理，则不能组成三角形，此项不符题意；
故答案为：C．
【分析】根据三角形的三边关系判断是否能组成三角形即可作答。
3.【答案】 A
【解析】【解答】解：∵点A关于x轴的对称点为A1（3，-2），
∴点A的坐标为（3，2），
故答案为：A．
【分析】根据关于x轴对称的点的坐标横坐标相等，纵坐标互为相反数即可求出点A的坐标。
4.【答案】 B
【解析】【解答】∵一个多边形的每一个外角都等于36°，
∴多边形的边数为360°÷36°=10．
故答案为：B.
【分析】多边形的外角和是固定的360°，依此可以求出多边形的边数.
5.【答案】 C
【解析】【解答】∵点到三角形三个顶点的距离相等，∴这个点一定是三角形三条边的垂直平分线的交点.
故答案为：C.
【分析】抓住已知条件：三角形的内部，有一个点到三角形三个顶点的距离相等，利用线段垂直平分线的判定定理，可得答案。
6.【答案】 B
【解析】【解答】解：甲三角形只知道一条边长、一个内角度数无法判断是否与△ABC全等；
乙三角形夹50°内角的两边分别与已知三角形对应相等，故乙与△ABC全等；
丙三角形72°内角及所对边与△ABC对应相等且均有50°内角，可根据AAS判定乙与△ABC全等；
则与△ABC全等的有乙和丙，
故答案为：B．
【分析】根据三角形全等的判定方法进行作答即可。
7.【答案】 D
【解析】【解答】解：∵AD∥BC，
∴∠EAD=∠B=32°，
∵AD是△ABC的外角∠EAC的平分线，
∴∠EAC=2∠EAD=64°，
∵∠EAC是△ABC的外角，
∴∠C=∠EAC-∠B=64°-32°=32°，
故答案为：D．
【分析】根据平行线的性质及三角形的外角的性质求出∠C的度数即可。
8.【答案】 D
【解析】【解答】解：∵EF∥BC，
∴∠EDB=∠DBC，∠EDC=∠DCB，
∵BD、CD分别平分∠ABC ， ∠ACB ，
∴∠EBD=∠DBC，∠DCB=∠DCF，
∴∠EBD=∠EDB，∠DCF=∠FDC，
∴DE=EB，DF=FC，
∴△AEF周长=AE+DE+AF+DF=AE+EB+AF+FC=AB+AC=15.
故答案为：D
【分析】根据平行线的性质及角平分线的定义得到DE=EB，DF=FC，再求三角形的周长即可。
9.【答案】 D
【解析】【解答】解：∵ ，
∴OE是∠AOB的角平分线，
又∵ 于点C， 于点G，
∴EC=EG=3，
∵ ，
∴∠EFG=∠AOE+∠BOE=30°，
∵ 于点G，
∴EF=2EG=6，
又∵∠EFG=∠AOE+∠OEF=30°， ，
∴∠OEF=15°，
∴OF=FE=6.
故答案为：D
【分析】根据角平分线的性质及平行线的性质进行作答即可。
10.【答案】 B
【解析】【解答】解：根据折叠性质可知：CD=AC=3，BC= =4，∠ACE=∠DCE，∠BCF=∠ CF，CE⊥AB，
∴∠DCE+∠ CF=∠ACE+∠BCF，
∵∠ACB=90°，
∴∠ECF=45°，
又∵CE⊥AB，
∴△ECF是等腰直角三角形，
∴EF=CE，
又∵S△ABC= AC∙BC= AB∙CE，
∴AC∙BC=AB∙CE，
∵ ， ， ,
∴ ，
∴EF .
故答案为：B
【分析】根据折叠的性质得到线段相等和角相等，再根据S△ABC= AC∙BC= AB∙CE，求出EF的长度即可。
二、填空题
11.【答案】 900°
【解析】【解答】解：七边形的内角和是：180°×（7﹣2）=900°．
故答案为：900°．
【分析】由n边形的内角和是：180°（n﹣2），将n=7代入即可求得答案．
12.【答案】 17
【解析】【解答】解：分两种情况：
当3为底时，其它两边都为7，3、7、7可以构成三角形，周长为17；
当3为腰时，其它两边为3和7，3+3=6＜7，所以不能构成三角形，故舍去，
所以等腰三角形的周长为17．
故答案为：17．
【分析】因为边为3和7，没明确是底边还是腰，所以有两种情况，需要分类讨论．
13.【答案】 8cm
【解析】【解答】解：∵AB=AC，∠C=30°，
∴∠B=∠C=30°，∠BAC=120°，
∵ ，
∴∠DAC=30°，
又∵ ，
∴AD=CD=4cm，
在直角三角形ABD中，
∵∠B=30°，
∴BD=2AD=8cm.
【分析】根据AB=AC，∠C=30°，， 求出∠DAC=30°，再求出BD的长度即可。
14.【答案】 25°
【解析】【解答】解：在△ABC中,
∵∠A=65°,∠B=45°，
∴∠ACB=180°−∠A−∠B=70°，
∵DE是BC的垂直平分线，
∴DB=DC，
∴∠DCB=∠B=45°，
∴∠ACD=∠ACB−∠DCB=70°−45°=25°.
故答案为25°.
【分析】根据三角形的内角和等于180°，求出∠ACB的度数，再根据线段垂直平分线的性质得到DB=DC，即可得到角相等，最后求出∠ACD的度数即可。
15.【答案】 （3，3）
【解析】【解答】解：已知∠OCB=90°，OC=BC
∴△OBC为等腰直角三角形，
∵顶点O（0，0），B（-6，0）
∴OB=6
过点C作CD⊥OB于点D，
OD=BD=3
∵∠OCB=90°，
∴OD=DC=3
∴C点坐标为（-3，3），
∴点C关于y轴对称的点的坐标是（3，3）
故答案为（3，3）
【分析】根据等腰三角形的性质再利用平面直角坐标系求出点的坐标即可。
16.【答案】 180
【解析】【解答】解：∵多边形的外角和为360°，
∴边数= =12，
即12×15米=180米，
故答案为：180．
【分析】根据多边形的外角和等于360°，求出多边形的边数，再作答即可。
17.【答案】 （2,4）或（-2,0）或（-2,4）
【解析】【解答】解：如图所示：
有三个点符合，
∵点A（2，0），B（0，4），
∴OB=4，OA=2，
若 ≌ ，
∴OA=OC1=2
∴C1（-2，0）；
若 ≌ ，
∴OA=BC2=2，∠OBC2=∠BOA=90°
∴C2（-2，4）；
若 ≌ ，
∴OA=BC3=2，∠OBC3=∠BOA=90°
∴C3（2，4）；
综上：点C的坐标为（2，4）或（-2，0）或（-2，4）
故答案为：（2，4）或（-2，0）或（-2，4）.
【分析】 本题考查了坐标与图形性质，全等三角形的判定与性质，难点在于根据点C的位置分情况讨论． 分点C在x轴负半轴上和点C在第一象限，第二象限三种情况，利用全等三角形对应边相等的性质进行解答，即可求解．
18.【答案】 4
【解析】【解答】作DG⊥BE于G，CF⊥AE于F，
∴∠DGE=∠CFE=90°，
∵∠AEB=∠DEC=90°，
∴∠GED+∠DEF=90°，∠DEF+∠CEF=90°，
∴∠GED=∠CEF，
又∵DE=EC，
∴△GDE≌△FCE，
∴DG=CF，
∵S△BED= BE•DG，S△AEC= AE•CF，AE=BE，
∴S△BED=S△AEC ，
∵D是BC的中点，
∴S△BDE=S△EDC= =2，
∴S阴影=2+2=4，
故答案为4.
【分析】作DG⊥BE于G，CF⊥AE于F，可证△DEG≌△CEF，可得DG=CF，则是S△BDE=S△AEC ， 由D是BC中点可得S△BED=2，即可求得阴影部分面积.
三、解答题
19.【答案】 （1）解：如图，点D即为所求．
（2）解：由（1）可知D在AC的垂直平分线上，
∴AD=CD，
∴∠A=∠ACD，
设∠A=x，
∴∠ACD=x，
∴∠BDC=∠A+∠ACD=2x，
∵CD=CB，
∴∠B=∠BDC=2x，
∵AB=AC，
∴∠ACB=∠B=2x，
∵∠A+∠B+∠ACB=180°，
即x+2x+2x=180°，
解得：x=36，
∴∠B=2x=72°．
【解析】【分析】根据尺规作图的方法作图即可；再根据线段垂直平分线的性质及三角形的内角和等于180°，进行作答即可。
20.【答案】 （1）解：∵△ACB与△DCE均为等腰直角三角形，
∴CA=CB，CD=CE，∠ACB=∠DCE=90°，
∴∠ACD=∠BCE，
在△ACD与△BCE中，
∵CA=BC，∠ACD=∠BDE，CD=CE，
∴△ACD≌△BCE(SAS)，
∴∠ADC=∠BEC，AD=BE，
∵△DCE为等腰直角三角形，
∴∠CED=∠CDE=45°，
∵点A、D、E在同一战线上，
∴∠ADC=135°，
∴∠BEC=135°，
∴∠AEB=∠BEC-∠CED=90°.
（2）证明：由（1）可得△ACD≌△BCE(SAS)，
∴CD=CE，AD=BE，∠CDE=45°，
∵CD⊥DE，CD=CE，
∴2DM=DE，∠CMD=90°，
∵∠CDE=45°，
∴∠DCM=180°-∠CMD-∠CDE=45°，
∴∠DCM=∠CDE，
∴CM=DM，
∴DE=2DM=2CM,
∴AE=AD+DE=BE+2CM.
【解析】【分析】根据全等三角形的判定方法与性质及三角形的内角和等于180°进行作答即可。