2021年安徽省黄山市八年级上学期数学期中试卷

这是一份2021年安徽省黄山市八年级上学期数学期中试卷，共12页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
 八年级上学期数学期中试卷
一、单选题
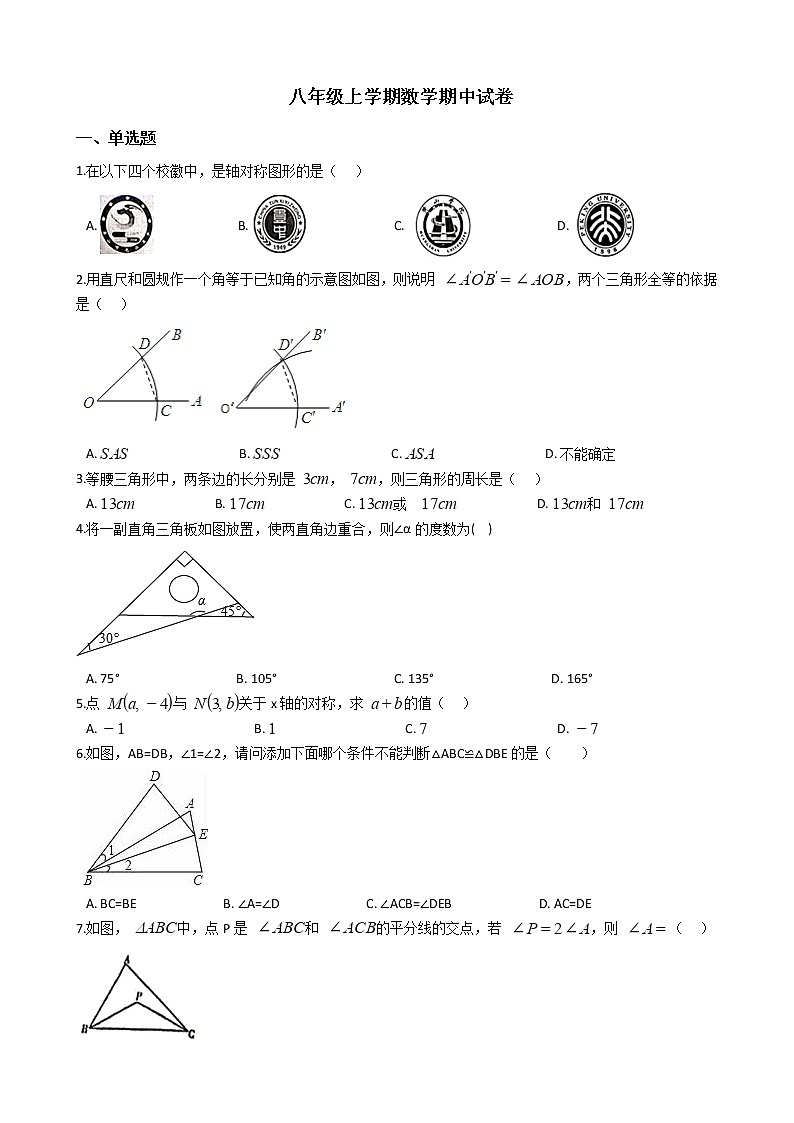
1.在以下四个校徽中，是轴对称图形的是（    ）
A.                           B.                           C.                           D. 
2.用直尺和圆规作一个角等于已知角的示意图如图，则说明 ，两个三角形全等的依据是（    ）

A.                                   B.                                   C.                                   D. 不能确定
3.等腰三角形中，两条边的长分别是 ， ，则三角形的周长是（    ）
A.                          B.                          C. 或                          D. 和
4.将一副直角三角板如图放置，使两直角边重合，则∠α的度数为(    )

A. 75°                                     B. 105°                                     C. 135°                                     D. 165°
5.点 与 关于x轴的对称，求 的值（    ）
A.                                          B.                                          C.                                          D. 
6.如图，AB=DB，∠1=∠2，请问添加下面哪个条件不能判断△ABC≌△DBE的是（　　）

A. BC=BE                           B. ∠A=∠D                           C. ∠ACB=∠DEB                           D. AC=DE
7.如图， 中，点P是 和 的平分线的交点，若 ，则 （    ）

A.                                     B.                                     C.                                     D. 
8.下列命题中真命题是（    ）
A. 三角形按边可分为不等边三角形，等腰三角形和等边三角形
B. 等边三角形有 条对称轴，它们是三条边上的高
C. 三角形的一个外角大于任何一个内角
D. 三角形三条内角平分线相交于一点，这点到三角形三边的距离相等
9.等腰三角形一腰上的高与底边所成的角等于（      ）

A. 顶角                           B. 顶角的2倍                           C. 顶角的一半                           D. 底角的一半
10.如图，已知 中， ， ，点 为 的中点，如果点 在线段 上以 的速度由点 向 点运动，同时，点 在线段 上由点 向 点以 的速度运动.经过(    )秒后， 与 全等.

A. 2                                      B. 3                                      C. 2或3                                      D. 无法确定
二、填空题
11.我们用如图的方法（斜钉上一块木条）来修理一条摇晃的凳子的数学原理是利用三角形的________.

12.在平面镜里看到背后墙上的电子钟示数如图所示，这时的实际时间应该是      .

13.在 中， ， ， 是 的中线，设 长为m，则m的取值范围是________．
14.如图的三角形纸片中， ，沿过点 的直线折叠这个三角形，使点 落在 边上的点 处，折痕为 ，则 的周长为________.

15.如图， 的面积为 ，以顶点A为圆心，适当长为半径画弧，分别交 ， 于点M，N，再分别以点M，N为圆心，大于 的长为半径画弧，两弧交于点P，作射线 ，过点C作 于点D，连接 ，则 的面积是________ ．

16.如图，已知 中， ， ，直角 的顶点P是 中点，两边 ． 分别交 ． 于点E．F，给出下列四个结论：① ；② 是等腰直角三角形；③ ；④四边形 的面积随着点E．F的位置不同发生变化，当 在 内绕顶点P旋转时（点E不与A．B重合），上述结论中始终正确的有________（把你认为正确的结论的序号都填上）．

三、解答题
17.一个多边形的内角和比它的外角和的2倍还大180度，求这个多边形的边数.
18.在 △ABC中，∠BAC=50°，∠B=45°，AD是△ABC的一条角平分线，求∠ADB的度数

19.已知：如图，△ABC中，D是BC边上一点，EB=EC ， ∠ABE=∠ACE ，
求证：∠BAE=∠CAE.

20.如图， 三个顶点的坐标分别为A(-2，2)， ， ．

⑴画出 关于y轴对称的 ；
⑵在y轴上画出点Q，使 最小．并直接写出点Q的坐标．
21.如图，△ABC中，AB=11，AC=5，∠BAC的平分线AD与边BC的垂直平分线DG相交于点D，过点D分别作DE⊥AB，DF⊥AC，垂足分别为E、F，求BE的长度.

22.如图，在 中， ， ，D是 边上一动点， 于E．

（1）如图（1），若 平分 时，
①求 的度数；
②延长 交 的延长线于点F，补全图形，探究 与 的数量关系，并证明你的结论；
（2）如图（2），过点A作 于点F，猜想线段 ， ， 之间的数量关系，并证明你的猜想．

答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解：由轴对称图形的概念可得A、B、C都不是轴对称图形，D选项是轴对称图形，
故答案为：D．
【分析】 轴对称图形，是指在平面内沿一条直线折叠，直线两旁的部分能够完全重合的图形，这条直线就叫做对称轴。 根据轴对称图形的定义作答即可。
2.【答案】 B
【解析】【解答】解：由题意可得：
在 和 中，
，
∴ ≌ （SSS），
故答案为：B．
【分析】根据全等三角形的判定方法进行作答即可。
3.【答案】 B
【解析】【解答】解：①3是腰长时，三角形的三边分别为7、3、3，
3+3=6＜7，不能组成三角形；
②3是底边长时，三角形的三边分别为7、7、3，
能组成三角形，周长=7+7+3=17，
综上所述，这个等腰三角形的周长是17，
故答案为：B．
【分析】分3是腰长与底边两种情况讨论求解．
4.【答案】 D
【解析】【解答】由三角形的外角性质得，∠1=45°+90°=135°，∠α=∠1+30°=135°+30°=165°.故答案为：D.
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和求出∠1，再求出∠α即可.
5.【答案】 C
【解析】【解答】解：由点 与 关于x轴的对称，可得：
，
∴ ；
故答案为：C．
【分析】根据关于x轴对称的点的横坐标相等，纵坐标互为相反数进行作答即可。
6.【答案】 D
【解析】【解答】A、添加BC=BE，可根据SAS判定△ABC≌△DBE，故正确；B、添加∠ACB=∠DEB，可根据ASA判定△ABC≌△DBE，故正确．C、添加∠A=∠D，可根据ASA判定△ABC≌△DBE，故正确；D、添加AC=DE，SSA不能判定△ABC≌△DBE，故错误；
添加∠ACB=∠DEB，可根据ASA判定△ABC≌△DBE，故正确．
故答案为：D．
【分析】由题干来看可以找出两三角形中已经具有一边对应相等，一组角对应相等，且边是夹相等角的一条边，故根据全等三角形的判定方法，只需要添加任意一个角对应相等，或者是添加夹相等角的另一条边对应相等即可，从而即可一一判断得出答案。
7.【答案】 B
【解析】【解答】解：∵点P是 和 的平分线的交点，
∴∠ABP=∠PBC，∠ACP=∠PCB，
∵∠A+∠ABC+∠ACB=180°，∠PBC+∠PCB+∠P=180°，
∴ ，
∴ ，
∴ ；
故答案为：B．
【分析】根据角平分线的定义及三角形的内角和等于180°，进行作答即可。
8.【答案】 D
【解析】【解答】解：A、三角形按边可分为不等边三角形，等腰三角形，故不符合题意，是假命题；
B、等边三角形有3条对称轴，它们是三条经过边上的高的直线，故不符合题意，是假命题；
C、三角形的一个外角大于任何一个与它不相邻的内角，故不符合题意，是假命题；
D、三角形三条内角平分线相交于一点，这点到三角形三边的距离相等，是真命题；
故答案为：D．
【分析】根据真命题的定义对每个选项进行判断即可。
9.【答案】 C
【解析】
【分析】作出图象根据等腰三角形两底角相等、三角形内角和定理和直角三角形两锐角互余列式求解．
【解答】

△ABC中，∵AB=AC，BD是高，
∴∠ABC=∠C=
在Rt△BDC中，∠CBD=90°-∠C=90°-=．
故选C．
【点评】本题考查了等腰三角形的性质：等边对等角，以及直角三角形两锐角互余的性质．题目本身是规律性的结论，要注意总结掌握，在今后的分析问题时可直接应用
10.【答案】 A
【解析】【解答】解：△BPD≌△CQP,理由如下：
当P，Q两点分别从B，A两点同时出发运动2秒时，

有BP=2×2=4cm，AQ=4×2=8cm，
则CP=BC-BP=10-4=6cm，CQ=AC-AQ=12-8=4cm．
∵D是AB的中点，
∴BD= AB= ×12=6cm，
∴BP=CQ，BD=CP，
又∵△ABC中，AB=AC，
∴∠B=∠C．
在△BPD和△CQP中，
BP=CQ，∠B=∠C，BD=CP，
∴△BPD≌△CQP（SAS）．
故答案为：A.
【分析】经过2秒后，PB=4cm，PC=6cm，CQ=4cm，由已知可得BD=PC，BP=CQ，∠ABC=∠ACB，即据SAS可证得△BPD≌△CQP．
二、填空题
11.【答案】 稳定性
【解析】【解答】用如图的方法（斜钉上一块木条）来修理一条摇晃的凳子的数学原理是利用三角形的稳定性，故答案为：稳定性.
【分析】考查三角形的稳定性。
12.【答案】 21:05
【解析】【解答】解：因为镜子中的成像与实际物体是相反的，利用轴对称性质作出图像向右的对称图

故答案为：21:05.
【分析】根据镜子中的成像与实际物体是相反的原理，可利用轴对称性质作出图像向左或向右的对称图形即可得出答案.
13.【答案】
【解析】【解答】解：如图，延长AD至点E，使 ，连接CE，

则 ，
是 的中线，
，
在 和 中， ，
，
，
在 中，由三角形的三边关系定理得： ，
，
，
解得 ，
故答案为： ．
【分析】根据全等三角形的判定方法及三角形的三边关系求m的取值范围即可。
14.【答案】 7cm
【解析】【解答】∵沿过点 的直线折叠这个三角形，使点 落在 边上的点 处，折痕为 ，
∴BE=BC，DE=DC，
∴ 的周长=AD+DE+AE=AD+DC+AE=AC+AE=AB+BC+AC-BC-BE=8+6+5-6-6=7cm，
故答案是：
【分析】由折叠的性质，可知：BE=BC，DE=DC，通过等量代换，即可得到答案.
15.【答案】 6
【解析】【解答】解：延长CD，交AB于点E，如图所示：

由题意可得AP平分∠CAB，
∴∠CAD=∠EAD，
∵CD⊥AD，
∴∠CDA=∠EDA=90°，
∵AD=AD，
∴△CDA≌△EDA（ASA），
∴CD=DE，
∴ ，
∴ ，
∵ ，
∴ ；
故答案为6．
【分析】延长CD，交AB于点E，由题意易得CD=DE，进而根据三角形的中线与面积的关系可求解．
16.【答案】 ①②
【解析】【解答】解：∵∠APE、∠CPF都是∠APF的余角，
∴∠APE＝∠CPF，
∵AB＝AC，∠BAC＝90°，P是BC中点，
∴AP＝CP，
又∵AP＝CP，∠EPA＝∠FPC，∠EAP＝∠FCP＝45°
∴△APE≌△CPF（ASA），同理可证△APF≌△BPE，
∴AE＝CF，△EPF是等腰直角三角形，S四边形AEPF＝ S△ABC ， ①②符合题意，④不符合题意，四边形 的面积是固定的；
∵旋转过程中，EF的长度的变化的，故EF≠AB，③不符合题意，
始终正确的是①②，
故答案为：①②．
【分析】根据三角形全等的判定与性质一一判断即可作答。
三、解答题
17.【答案】 解：设这个多边形的边数为n，
根据题意，得（n﹣2）×180°=2×360°+180°，
解得n=7．
故这个多边形的边数是7．
【解析】【分析】 设这个多边形的边数为n， 由于多边形内角和公式 （n﹣2）×180°，多边形外角和为360°，根据“ 一个多边形的内角和比它的外角和的2倍还大180度 ”列出方程并解出方程即可.
18.【答案】 解：∵AD是△ABC的一条角平分线，
∴∠BAD= ∠BAC= ×50°=25°，
∴∠ADB＝180°-∠BAD-∠B=180°-25°-45°＝110°．
【解析】【分析】根据角平分线的定义及三角形的内角和求出∠ADB的度数即可作答。
19.【答案】 证明：∵EB=EC
∴∠EBC=∠ECB
∴∠ABE=∠ACE
∴∠ABD=∠ACD
∴AB=AC
∵AE=AE
∴△ABE≌△ACE（SSS）
∴∠BAE=∠CAE
【解析】【分析】根据 EB=EC ，得到 ∠EBC=∠ECB ，再根据全等三角形的判定与性质进行作答即可。
20.【答案】 解：（1）如图，△A1B1C1为所求．（2）如图，Q（0，0）

【解析】【分析】根据关于y轴对称的点的坐标特点求出点的坐标，作出三角形即可。再观察图，根据两点间线段最短，求出点Q的坐标即可得解。
21.【答案】 如图，连接CD，BD，

∵AD是∠BAC的平分线，DE⊥AB，DF⊥AC，
∴DF=DE,∠F=∠DEB=90°，∠ADF=∠ADE，
∴AE=AF，
∵DG是BC的垂直平分线，
∴CD=BD，
在Rt△CDF和Rt△BDE中，
，
∴Rt△CDF≌Rt△BDE（HL），
∴BE=CF，
∴AB=AE+BE=AF+BE=AC+CF+BE=AC+2BE，
∵AB=11，AC=5，
∴BE= ×（11-5）=3．
【解析】【分析】连接CD，BD，由角平分线定理得到DF=DE，∠F=∠DEB=90°，∠ADF=∠ADE，由DG是BC的垂直平分线得到CD=BD，由此证明Rt△CDF≌Rt△BDE，推出BE=CF，再根据AB=11 ， AC= 5即可求出答案.
22.【答案】 （1）解：∵ ， ，
∴∠ABC=∠ACB=45°，
∵BD平分∠ABC，
∴∠CBD=∠ABD=22.5°，
①∵∠ABD+∠BDA=∠CDE+∠ECD=90°，∠CDE=∠BDA，
∴∠ABD=∠ECD=22.5°；
②BD=2EC，理由如下：如图所示：

∵ ，
∴∠CEB=∠FEB=90°，
∵BE=BE，
∴△CEB≌△FEB（ASA），
∴CE=FE，
∵∠DBA+∠F=90°，∠FCA+∠F=90°，
∴∠DBA=∠FCA，
∵∠BAD=∠CAF=90°，AB=AC，
∴△ABD≌△ACF（ASA），
∴BD=CF，
∴BD=2CE；

（2）解：BE=CE+2AF，理由如下：
在BE上截取BH=CE，连接AH，如图，

由（1）易得∠HBA=∠ECA，
∵AB=AC，
∴△BHA≌△CEA（SAS），
∴AH=AE，∠BAH=∠CAE，
∵∠BAH+∠HAC=90°，
∴∠EAC+∠HAC=90°，即∠HAE=90°，
∵AF⊥BE，
∴AF=HF=FE，
∵BE=BH+HF+FE，
∴BE=CE+2AF．
【解析】【分析】根据角平分线的定义及三角形全等的判定与性质进行作答即可。