2021年陕西省宝鸡市八年级上学期数学期中考试试题

这是一份2021年陕西省宝鸡市八年级上学期数学期中考试试题，共13页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

 八年级上学期数学期中考试试卷
一、单选题
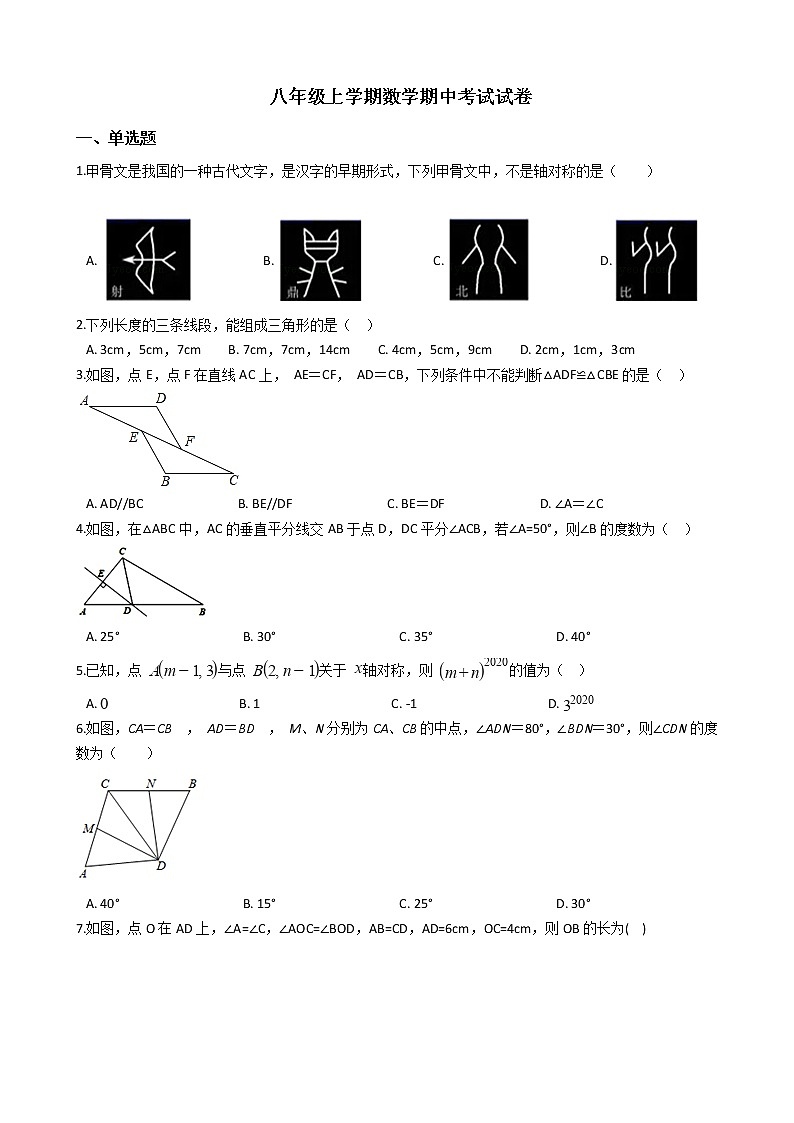
1.甲骨文是我国的一种古代文字，是汉字的早期形式，下列甲骨文中，不是轴对称的是（　　）

A.                      B.                      C.                      D. 
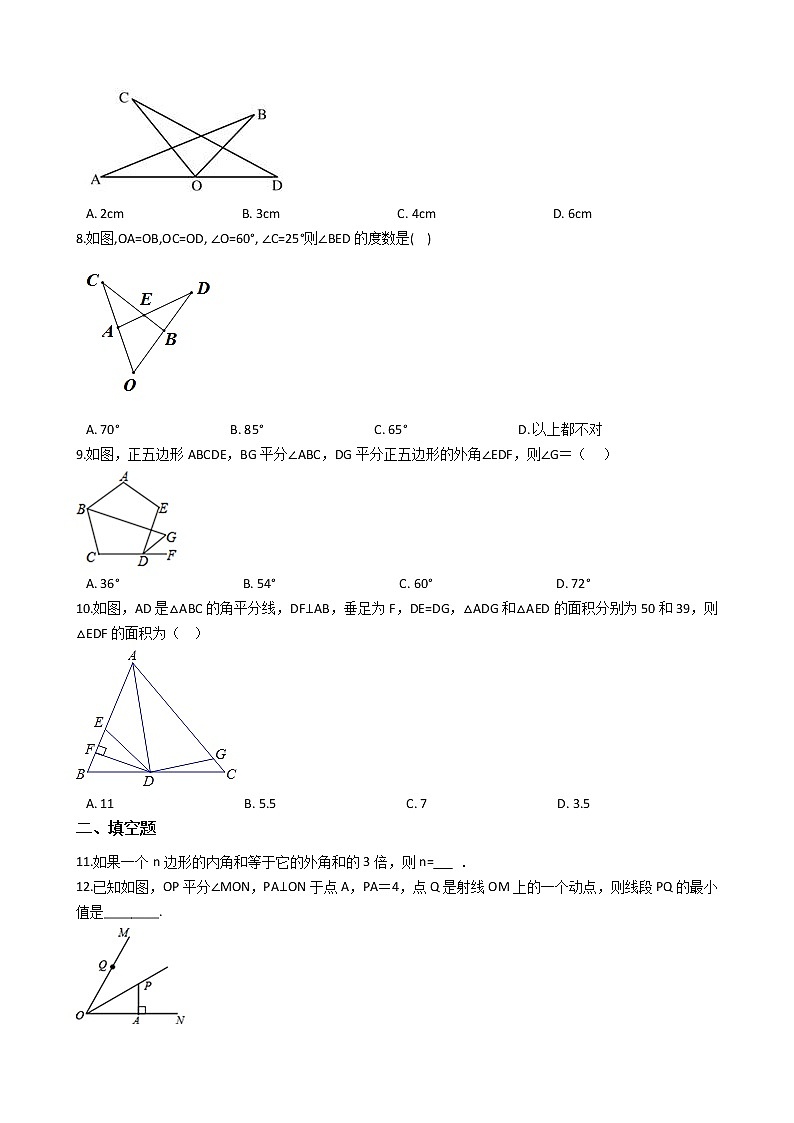
2.下列长度的三条线段，能组成三角形的是（   ）
A. 3cm，5cm，7cm        B. 7cm，7cm，14cm        C. 4cm，5cm，9cm        D. 2cm，1cm，3cm
3.如图，点E，点F在直线AC上， AE＝CF， AD＝CB，下列条件中不能判断△ADF≌△CBE的是（   ）

A. AD//BC                             B. BE//DF                             C. BE＝DF                             D. ∠A＝∠C
4.如图，在△ABC中，AC的垂直平分线交AB于点D，DC平分∠ACB，若∠A=50°，则∠B的度数为（   ）

A. 25°                                       B. 30°                                       C. 35°                                       D. 40°
5.已知，点 与点 关于 轴对称，则 的值为（   ）
A.                                          B. 1                                         C. -1                                         D. 
6.如图，CA＝CB ， AD＝BD ， M、N分别为CA、CB的中点，∠ADN＝80°，∠BDN＝30°，则∠CDN的度数为（　　）

A. 40°                                       B. 15°                                       C. 25°                                       D. 30°
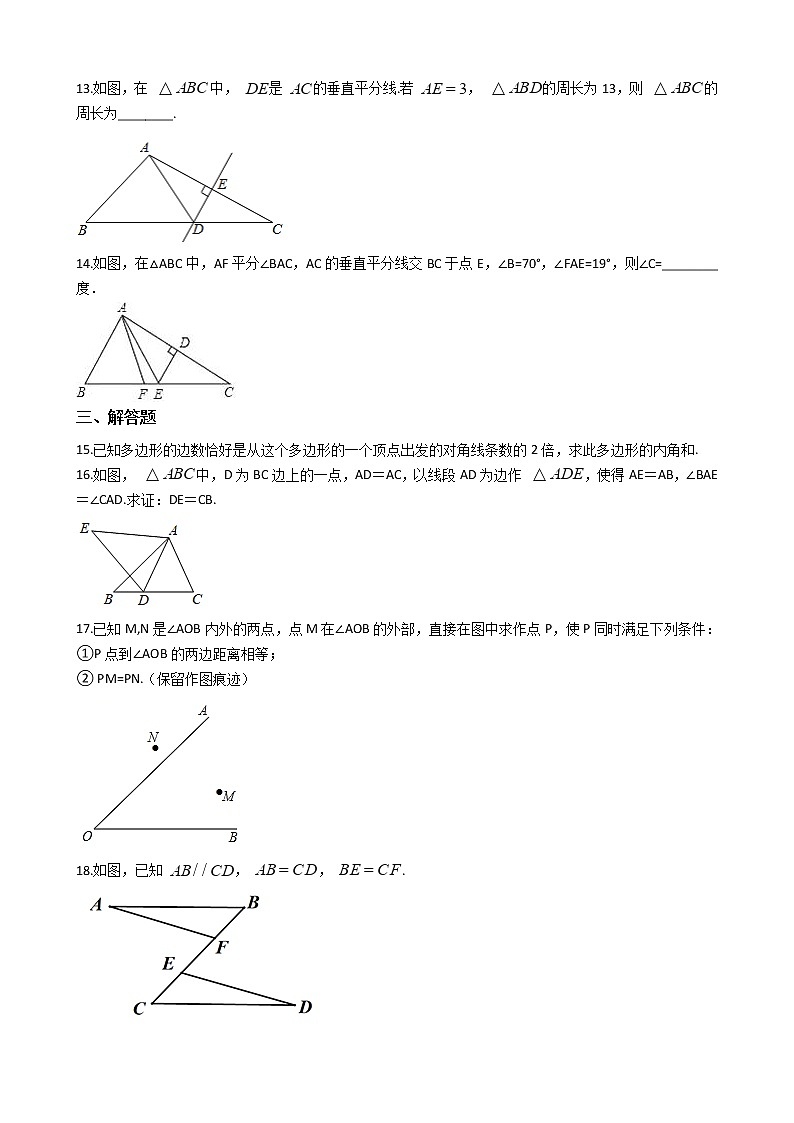
7.如图，点O在AD上，∠A=∠C，∠AOC=∠BOD，AB=CD，AD=6cm，OC=4cm，则OB的长为(    )

A. 2cm                                     B. 3cm                                     C. 4cm                                     D. 6cm
8.如图,OA=OB,OC=OD, ∠O=60°, ∠C=25°则∠BED的度数是(    )

A. 70°                                   B. 85°                                   C. 65°                                   D. 以上都不对
9.如图，正五边形ABCDE，BG平分∠ABC，DG平分正五边形的外角∠EDF，则∠G＝（    ）

A. 36°                                       B. 54°                                       C. 60°                                       D. 72°
10.如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为（   ）

A. 11                                         B. 5.5                                         C. 7                                         D. 3.5
二、填空题
11.如果一个n边形的内角和等于它的外角和的3倍，则n=       ．
12.已知如图，OP平分∠MON，PA⊥ON于点A，PA＝4，点Q是射线OM上的一个动点，则线段PQ的最小值是________.

13.如图，在 中， 是 的垂直平分线.若 ， 的周长为13，则 的周长为________.

14.如图，在△ABC中，AF平分∠BAC，AC的垂直平分线交BC于点E，∠B=70°，∠FAE=19°，则∠C=________度．

三、解答题
15.已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍，求此多边形的内角和.
16.如图， 中，D为BC边上的一点，AD＝AC，以线段AD为边作 ，使得AE＝AB，∠BAE＝∠CAD.求证：DE＝CB.

17.已知M,N是∠AOB内外的两点，点M在∠AOB的外部，直接在图中求作点P，使P同时满足下列条件：
①P点到∠AOB的两边距离相等；
② PM=PN.（保留作图痕迹）

18.如图，已知 ， ， .

 
求证：
（1）；
（2）.
19.如图，在△ABE中，AD⊥BE于点D，C是BE上一点，BD＝DC，且点C在AE的垂直平分线上，若△ABC的周长为18 cm，求DE的长.

20.若点C（-2，-3）关于x轴的对称点为A，关于y轴的对称点为B.

（ 1 ）在坐标系xOy中画出△ABC，并求△ABC的面积；
（ 2 ）将△ABC向上移2个单位，再向右移4个单位得到△A1B1C1 ， 画出△A1B1C1 ， 并写出A1 ， B1 ， C1的坐标.
21.如图，点D是△ABC边AC上一点，AD=AB，过B点作BE∥AD，且BE=CD，连接CE交BD于点O，连接AO.求证：AO平分∠BAC.

22.如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．

（1）.说明BE=CF的理由；
（2）.如果AB=5，AC=3，求AE、BE的长．

答案解析部分
一、单选题
1.【答案】 D
【解析】【解答】解：A、是轴对称图形，故本选项错误；

B、是轴对称图形，故本选项错误；
C、是轴对称图形，故本选项错误；
D、不是轴对称图形，故本选项正确．
故选D．
【分析】根据轴对称图形的概念求解．本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．
2.【答案】 A
【解析】【解答】解：根据三角形任意两边的和大于第三边，得
A中，3+5＞7，能组成三角形；
B中，7+7=14，不能组成三角形；
C中，4+5=9，不能够组成三角形；
D中，2+1=3，不能组成三角形.
故答案为：A.
【分析】两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形.根据三角形的三边关系进行分析判断即可.
3.【答案】 B
【解析】【解答】解：∵AE=CF，则AF=CE，
A、添加AD//BC，可得∠A=∠C，由全等三角形的判定定理SAS可以判定△ADF≌△CBE，故本选项错误；
B、添加BE//DF，可得∠DFA=∠BEC，由全等三角形的判定定理不能判定△ADF≌△CBE，故本选项正确；
C、添加BE＝DF，由全等三角形的判定定理SSS可以判定△ADF≌△CBE，故本选项错误；
D、添加∠A＝∠C，由全等三角形的判定定理SAS可以判定△ADF≌△CBE，故本选项错误；
故答案为：B.
【分析】在△ADF与△CBE中，AE＝CF， AD＝CB，所以结合全等三角形的判定方法分别分析四个选项即可.
4.【答案】 B
【解析】【解答】解：∵DE垂直平分AC，
∴AD=CD，
∴∠ACD=∠A=50°
又∵CD平分∠ACB，
∴∠ACB=2∠ACD=100°，
∴∠B=180°-∠A-∠ACB=180°-50°-100°=30°，
故答案为：B.
【分析】依据线段垂直平分线的性质，即可得到AD=CD，根据等边对等角得∠A=∠ACD，再根据角平分线的定义，即可得出∠ACB的度数，根据三角形内角和定理，即可得到∠B的度数.
5.【答案】 B
【解析】【解答】∵点 与点 关于 轴对称，
∴ ，
∴ ，
∴ ，
故答案为：B.
【分析】根据关于x轴对称的点的横坐标相同，纵坐标互为相反数可得到m、n的值，代入求值即可.
6.【答案】 C
【解析】【解答】解：在△CAD和△CBD中，
，
∴△CAD≌△CBD（SSS），
∴∠CDA=∠CDB，∠A=∠B，
又∵AC=CB，M，N分别为CA，CB的中点，
∴AM=BN，又AD=BD，
∴△ADM≌△BDN（SAS），
∴∠ADM=∠BDN=30°，
∵∠ADN=80°，
∴∠ADM+2∠CDN=80°，
∴∠CDN=25°，
故答案为：C．
【分析】由“SSS”可证△CAD≌△CBD，可得∠CDA=∠CDB，∠A=∠B，由“SAS”可证△ADM≌△BDN，可得∠ADM=∠BDN=30°，即可求解．
7.【答案】 A
【解析】【解答】解：∵∠AOC=∠BOD
∴∠AOC+∠COB=∠BOD+∠COB
∴∠AOB=∠COD
∵∠A=∠C，AB=CD
∴△AOB≌△COD
∴OA=OC=4，OB=OD
∵OD=6-4=2
∴OB=2.
故答案为：A.
【分析】根据全等三角形的性质证明△AOB≌△COD，得到OA=OC，OB=OD，利用线段的和差关系，即可得到OB的长度。
8.【答案】 A
【解析】【解答】解：在△OAD和△OBC中
，
∴△OAD≌△OBC(SAS)，
∴∠D=∠C.
∵∠C=25°，
∴∠D=25°.
∵∠O=60°，
∴∠OBC=95°.
∵∠BED+∠D=∠OBC，
∴∠BED+25°=95°，
∴∠BED=70°.
故答案为：A.
【分析】由题意用边角边可证△OAD≌△OBC，由全等三角形的对应角相等可得∠D=∠C，根据直角三角形的两锐角互余可求得∠OBC的度数，再根据三角形的一个外角等于和它不相邻的两个内角之和得∠BED+∠D=∠OBC，则∠BED的度数可求解.
9.【答案】 B
【解析】【解答】∵正五边形外角和为360°，∴外角 ，
∴内角 ，
∵BG平分∠ABC，DG平分正五边形的外角∠EDF
∴ ，
在四边形BCDG中，
故答案为：B.
【分析】先求出正五边形一个的外角，再求出内角度数，然后在四边形BCDG中，利用四边形内角和求出∠G.
10.【答案】 B
【解析】【解答】解：作DM=DE交AC于M，作DN⊥AC于点N，
∵DE=DG，
∴DM=DG，
∵AD是△ABC的角平分线，DF⊥AB，
∴DF=DN，
在Rt△DEF和Rt△DMN中，
，
∴Rt△DEF≌Rt△DMN（HL），
∵△ADG和△AED的面积分别为50和39，
∴S△MDG=S△ADG﹣S△ADM=50﹣39=11，
S△DNM=S△EDF= S△MDG= ×11=5.5．
故选B．

【分析】作DM=DE交AC于M，作DN⊥AC，利用角平分线的性质得到DN=DF，将三角形EDF的面积转化为三角形DNM的面积来求．
二、填空题
11.【答案】 8
【解析】【解答】解：由题意得：180（n﹣2）=360×3，
解得：n=8，
故答案为：8．
【分析】根据多边形内角和公式180°（n﹣2）和外角和为360°可得方程180（n﹣2）=360×3，再解方程即可．
12.【答案】 4
【解析】【解答】解：当PQ⊥OM时，PQ有最小值.

∵OP平分∠MON，PA⊥ON于点A，PA=4，
∴PQ=PA=4，
故答案为：4.
【分析】先判断Q点的位置，再根据角平分线上的点到角两边的距离相等可求解线段PQ的最小值.
13.【答案】 19
【解析】【解答】解： 是 的垂直平分线. ，
 
 
的周长
 
故答案为：19
【分析】由线段的垂直平分线的性质可得 ，从而可得答案.
14.【答案】 24
【解析】【解答】解：∵DE是AC的垂直平分线，
∴EA=EC，
∴∠EAC=∠C，
∴∠FAC=∠EAC+19°，
∵AF平分∠BAC，
∴∠FAB=∠EAC+19°，
∵∠B+∠BAC+∠C=180°，
∴70°+2（∠C+19°）+∠C=180°，
解得，∠C=24°，
故答案为：24．
【分析】根据中垂线的性质得出EA=EC，根据等边对等角得出∠EAC=∠C，根据角的和差得出∠FAC=∠EAC+19°，根据角平分线的定义得出∠FAB=∠EAC+19°，根据三角形的内角和列出方程，求解得出答案。
三、解答题
15.【答案】 解：设多边形的边数为n，
则n＝2(n-3)，
解得n＝6，
∴(n-2)×180=4×180=720度.
【解析】【分析】设此多边形有n条边，则从一个顶点引出的对角线有(n-3)条，根据“一个多边形的边数恰好是从一个顶点引出的对角线条数的2倍”列出方程，解方程得出该多边形的边数，进而根据多边形的内角和公式即可出答案.
16.【答案】 证明：∵∠BAE＝∠CAD，
∴∠BAE+∠BAD＝∠CAD+∠BAD，
即∠DAE＝∠CAB，
在△ADE和△ACB中，
，
∴△ADE≌△ACB（SAS），
∴DE＝CB.
【解析】【分析】先由角的和差性质证得∠DAE＝∠CAB，再根据SAS定理证明△ADE≌△ACB，最后根据全等三角形的对应边相等得出DE＝CB.
17.【答案】 解：如图所示：P点即为所求．

【解析】【分析】使P到点M、N的距离相等，即画MN的垂直平分线，且到∠AOB的两边的距离相等，即画它的角平分线，两线的交点就是点P的位置．
18.【答案】 （1）证明：∵AB∥CD，
∴∠B=∠C，
∵BE=CF，
∴BE-EF=CF-EF，
即BF=CE，
在△ABF和△DCE中，
 
∴△ABF≌△DCE（SAS）；

（2）证明：∵△ABF≌△DCE，
∴∠AFB=∠DEC，
∴∠AFE=∠DEF，
∴AF∥DE.
【解析】【分析】（1）先由平行线的性质得∠B=∠C，从而利用SAS判定△ABF≌△DCE；（2）根据全等三角形的性质得∠AFB=∠DEC，由等角的补角相等可得∠AFE=∠DEF，再由平行线的判定可得结论.
19.【答案】 解：∵点C在AE的垂直平分线上，
∴CA=CE，
∵AD⊥BE，BD=DC，
∴AB=AC，
∵△ABC的周长为18，
∴AB+BC+AC=18，
∴2AC+2DC=18，
∴AC+DC=9，
∴DE=DC+CE=AC+CD=9（cm）.
【解析】【分析】根据线段垂直平分线的性质得到CA=CE，AB=AC，根据三角形的周长公式计算，得到答案.
20.【答案】 解：作△ABC、△A1B1C1如图，

△ABC的面积＝ ×6×4＝12
 A1(2，5)，B1(6，﹣1)，C1(2，﹣1).
【解析】【分析】（1）根据网格结构找出点C，再根据方格纸的特点及轴对称的性质找出点A、B的位置，然后顺次连接即可，再根据三角形的面积公式列式计算；
（2）根据网格结构找出平移后的点A1 ， B1 ， C1的位置，然后顺次连接即可，再根据平面直角坐标系写出A1 ， B1 ， C1的坐标.
21.【答案】 证明：∵BE∥AC，
∴∠E=∠DCO，在△BOE和△DOC中，

∴△BOE≌△DOC（AAS），
∴BO=OD，
∵AB=AD，
∴AO平分∠BAC.
【解析】【分析】根据平行线性质得到∠E=∠DCO，从而利用AAS即可判断出△BOE≌△DOC，利用全等三角形的对应边相等得出BO=OD，进而根据等腰三角形的三线合一即可得到结论.
22.【答案】 （1）证明：连接BD，CD，

∵ AD平分∠BAC，DE⊥AB，DF⊥AC，
∴DE=DF，∠BED=∠CFD=90°，
∵DG⊥BC且平分BC，
∴BD=CD，   
在Rt△BED与Rt△CFD中，
，   
∴Rt△BED≌Rt△CFD（HL），
∴BE=CF；   

（2）解：在△AED和△AFD中，
 
∴△AED≌△AFD（AAS），
∴AE=AF，
设BE=x，则CF=x，
∵AB=5，AC=3，AE=AB﹣BE，AF=AC+CF，
∴5﹣x=3+x，解得：x=1，  
∴BE=1，即AE=AB﹣BE=5﹣1=4．
【解析】【分析】（1）连接DB，DC，证明Rt△BED≌Rt△CFD，再运用全等三角形的性质即可证明；（2）.先证明△AED≌△AFD得到AE=AF，设BE=x，则CF=x， 利用线段的和差即可完成解答.