






冀教版九年级下册30.4 二次函数的应用习题ppt课件
展开1.【2019·河北邢台桥西区模拟】如图,在△ABC中,∠B=90°,AB=6 cm,BC=12 cm,动点P从点A开始沿边AB向点B以1 cm/s的速度移动(不与点B重合),动点Q从点B开始沿边BC向点C以2 cm/s的速度移动(Q不与点C重合).如果P,Q分别从A,B同时出发,那么当四边形APQC的面积最小时,经过的时间是( )A.1 s B.2 s C.3 s D.4 s
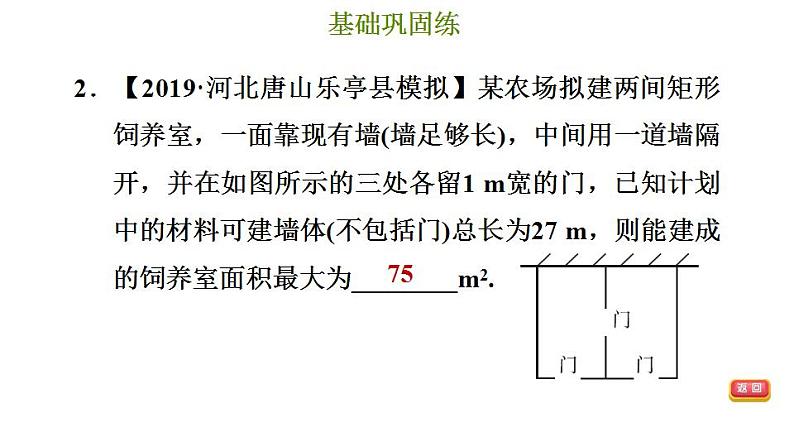
2.【2019·河北唐山乐亭县模拟】某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图所示的三处各留1 m宽的门,已知计划中的材料可建墙体(不包括门)总长为27 m,则能建成的饲养室面积最大为________m2.
3.出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,为了使一天出售该种手工艺品的总利润y(元)最大,则x的值为( )A.4 B.5 C.6 D.8
4.便民商店销售一种商品,在销售过程中,发现一周的利润y(单位:元)与每件销售价x(单位:元)之间的关系满足y=-2(x-20)2+1 558,由于某种原因,每件销售价x(单位:元)满足15≤x≤22,那么一周可获得的最大利润是________元.
5.某商场以每件42元的价钱购进一种服装,根据试销知,这种服装每天的销售量t(单位:件)与每件的销售价x(单位:元)满足一次函数关系式:t=-3x+204.(1)该商场卖这种服装每天的销售利润y(单位:元)与每件的销售价x(单位:元)之间的函数表达式为______________________;
y=-3x2+330x-8 568
(2)该商场要想每天获得最大销售利润,每件的销售价定为________元最合适,最大利润是________元.
6.已知某种礼炮的升空高度h(m)与飞行时间t(s)之间的关系满足h=-(t-4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )A.3 s B.4 s C.5 s D.6 s
7.【2020·山西】竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示,其中h0(m)是物体抛出时离地面的高度,v0(m/s)是物体抛出时的速度.某人将一个小球从距地面1.5 m的高处以20 m/s的速度竖直向上抛出,小球达到的离地面的最大高度为( )A.23.5 m B.22.5 m C.21.5 m D.20.5 m
8.【教材改编题】使用家用燃气灶烧开同一壶水所需的燃气量y(m3)与旋钮的旋转角度x(°)(0°<x≤90°)近似满足函数关系式y=ax2+bx+c(a≠0).下图记录了某种家用燃气灶烧开同一壶水所需的燃气量y与旋钮的旋转角度x的三组数据,根据上述函数模型和数据,可推断出此燃气灶烧开一壶水最节省燃气的旋钮的旋转角度约为( )
A.18° B.36° C.41° D.58°
9.【易错:忽略取值范围而致错】某地区一段时间内温度y与时间t的函数关系满足y=-t2+12t+2,当7≤t≤10时,该地区的最高温度是( )A.38℃ B.37℃ C.36℃ D.34℃
10.【教材改编题】某社区决定把一块长50 m,宽30 m的矩形空地建成居民健身广场,设计方案如图所示,阴影区域为绿化区(四块绿化区为大小、形状都相同的矩形),空白区域为活动区,且四周的4个出口宽度相同,其宽度不小于14 m,且不大于26 m,设绿化区较长边为x m,活动区的面积为y m2.小明同学根据出口宽度不小于14 m,得出x≤18.
(1)求y与x之间的函数表达式,并直接写出自变量x的取值范围;
解:根据题意,得绿化区的宽为[30-(50-2x)]÷2=x-10(m),∴y=50×30-4x(x-10)=-4x2+40x+1 500(12≤x≤18).
(2)求活动区的最大面积;
解:y=-4x2+40x+1 500=-4(x-5)2+1 600.∵-4<0,∴当12≤x≤18时,y随x的增大而减小,∴当x=12时,y取得最大值,最大值为1 404,即活动区的最大面积为1 404 m2.
(3)预计活动区造价为50元/m2,绿化区造价为40元/m2,若该社区的此项建造投资费用不得超过72 000元,求投资费用最少时活动区的出口宽度.
解:设投资费用为w元,由题意得w=50(-4x2+40x+1 500)+40×4x(x-10)=-40(x-5)2+76 000.当w=72 000时,解得x1=-5(不合题意,舍去),x2=15.
∵-40<0,12≤x≤18,∴当15≤x≤18时,w≤72 000.∵当15≤x≤18时,w随x的增大而减小,∴当x=18时,投资费用最少,此时活动区的出口宽度为50-2×18=14(m).
11.【2020·辽宁盘锦】某服装厂生产A品牌服装,每件成本为71元,零售商到此服装厂一次性批发A品牌服装x件时,批发单价为y元,y与x之间满足如图所示的函数关系,其中x为10的正整数倍.(1)当100≤x≤300时,y与x的函数表达式为_______________;
(2)某零售商到此服装厂一次性批发A品牌服装200件,需要支付多少元?
解:当x=200时,y=-20+110=90.∵90×200=18 000(元),∴需要支付18 000元.
(3)零售商到此服装厂一次性批发A品牌服装x(100≤x≤400)件,服装厂的利润为w元,问:x为何值时,w最大?最大值是多少?
12.【创新考法】有一块缺角矩形地皮ABCDE(如图①),其中AB=110 m,BC=80 m,CD=90 m,∠EDC=135°,现准备用此地建一座地基为长方形的数学大楼,建筑公司在接受任务后,设计了如图②所示的甲、乙、丙三种方案.
(1)求出甲、乙两种方案的地基面积;
解:方案甲的地基面积为80×90=7 200(m2);方案乙的地基面积为110×[80-(110-90)]=6 600(m2).
(2)若设地基的面积为S m2,宽为x m,求方案丙中S与x的表达式;
初中数学冀教版九年级下册30.4 二次函数的应用评课ppt课件: 这是一份初中数学冀教版九年级下册30.4 二次函数的应用评课ppt课件,共25页。PPT课件主要包含了30-x,20+x,∴0≤x<20,几何面积最值问题,一个关键,一个注意,建立函数关系式,最大利润问题,确定自变量取值范围,确定最大利润等内容,欢迎下载使用。
二次函的最值问题课件 九年级数学上册复习专题: 这是一份二次函的最值问题课件 九年级数学上册复习专题,共16页。PPT课件主要包含了变式练习等内容,欢迎下载使用。
数学中考总复习 二次函数的应用:用最值解决实际问题 精品课件: 这是一份数学中考总复习 二次函数的应用:用最值解决实际问题 精品课件,共20页。PPT课件主要包含了基础自主复习,s=40t-t2,自我检测一,函数的最值解决实,课后练习,填空题,解答题等内容,欢迎下载使用。













