高中数学北师大版必修13函数的单调性教学课件ppt

这是一份高中数学北师大版必修13函数的单调性教学课件ppt，共16页。PPT课件主要包含了创设情景兴趣导入，动脑思考探索新知，巩固知识典型例题，理论升华整体建构，环节设计，归纳总结，课后作业等内容，欢迎下载使用。
1.1 简单的绘图技巧
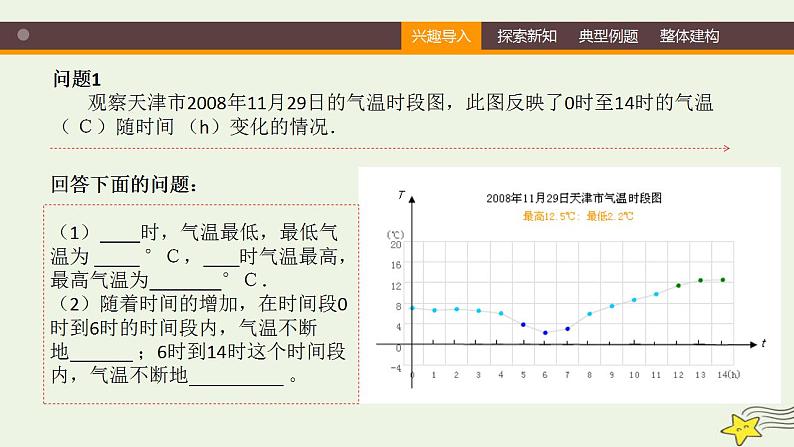
问题1 观察天津市2008年11月29日的气温时段图，此图反映了0时至14时的气温 （ Ｃ）随时间 （h）变化的情况．
回答下面的问题：（1） 时，气温最低，最低气温为 °Ｃ， 时气温最高，最高气温为 °Ｃ．（2）随着时间的增加，在时间段0时到6时的时间段内，气温不断地 ；6时到14时这个时间段内，气温不断地 。
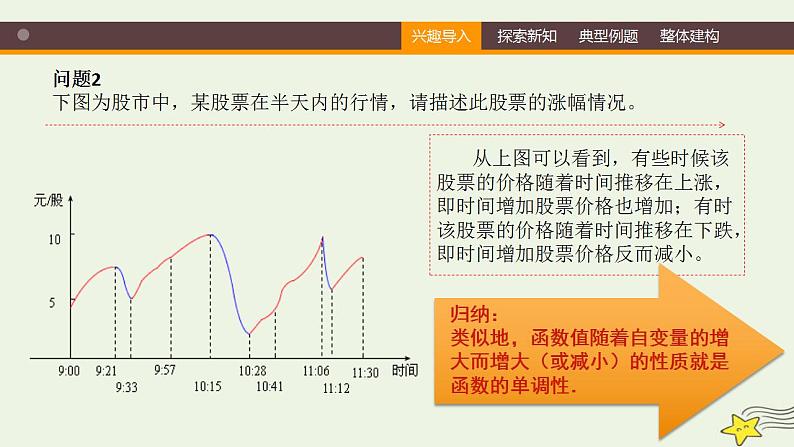
问题2下图为股市中，某股票在半天内的行情，请描述此股票的涨幅情况。
从上图可以看到，有些时候该股票的价格随着时间推移在上涨，即时间增加股票价格也增加；有时该股票的价格随着时间推移在下跌，即时间增加股票价格反而减小。
概念：函数值随着自变量的增大而增大（或减小）的性质叫做函数的单调性．
类型：设函数 在区间 内有意义．
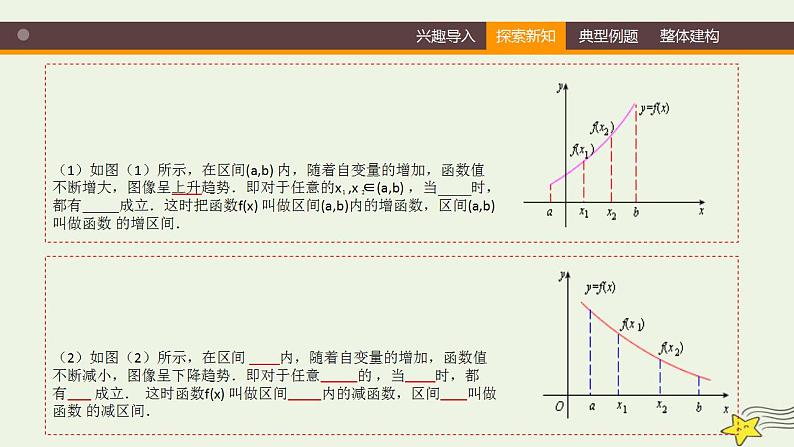
如果函数 在区间 内是增函数（或减函数），那么，就称函数 在区间 内具有单调性，区间 叫做函数 的单调区间．
几何特征：函数单调性的几何特征：在自变量取值区间上，顺着x轴的正方向，若函数的图像上升，则函数为增函数；若图像下降则函数为减函数．判定方法：判定函数的单调性有两种方法：借助于函数的图像或根据单调性的定义来判定．
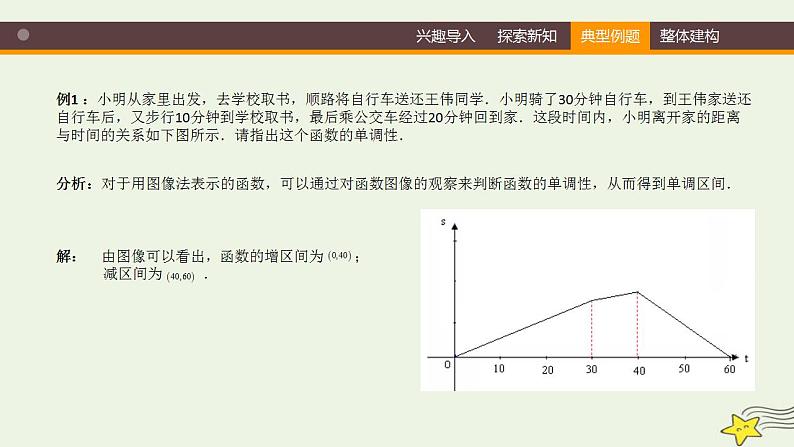
例1 ：小明从家里出发，去学校取书，顺路将自行车送还王伟同学．小明骑了30分钟自行车，到王伟家送还自行车后，又步行10分钟到学校取书，最后乘公交车经过20分钟回到家．这段时间内，小明离开家的距离与时间的关系如下图所示．请指出这个函数的单调性．
分析：对于用图像法表示的函数，可以通过对函数图像的观察来判断函数的单调性，从而得到单调区间．
例2 判断函数 的单调性．
分析 对于用解析式表示的函数，其单调性可以通过定义来判断，也可以作出函数的图像，通过观察图像来判断．无论采用哪种方法，都要首先确定函数的定义域．
在直角坐标系中，描出点（0，－2），（1，2），作出经过这两个点的直线．观察图像知函数 在 内为增函数．
解法2：师生根据定义共同完成。
由一次函数 （ ）的图像（如下图）可知：
（1）当 时，图像从左至右上升，函数是单调递增函数；（2）当 时，图像从左至右下降，函数是单调递减函数．
由反比例函数 的图像（如下图）可知：
（1）当 时，在各象限中 值分别随 值的增大而减小，函数是单调递减函数； （2）当 时，在各象限中 值分别随 值的增大而增大，函数是单调递增函数．
本次课学了哪些内容？重点和难点各是什么？
教材习题3.2 1、2