2020-2021学年第三章 函数概念与性质3.4 函数的应用（一）授课课件ppt

这是一份2020-2021学年第三章 函数概念与性质3.4 函数的应用（一）授课课件ppt，共17页。
1 | 几类常见的函数模型
2 | 利用函数模型解决实际问题的过程
1.解决某一实际问题的函数模型是唯一的. (    ✕　)2.对于一个实际问题,收集到的数据越多,建立的函数模型的模拟效果越好. (    √　)3.在实际问题中,若变量间的对应关系不能用一个关系式给出,则需构建分段函数 模型. (　√　)
1 | 如何解决已知函数模型的实际应用问题
在实际问题中,大多涉及的两个变量之间的关系符合已知函数模型,如一次函 数、二次函数、反比例函数、幂函数等,解决这种函数应用问题的常见步骤如 下:1.利用待定系数法求出函数解析式;2.根据函数解析式,结合题中需要研究的函数的性质解决实际问题.在函数模型中,二次函数模型占有重要的地位.在根据实际问题得到二次函数的 解析式后,可以利用配方法、换元法、函数的单调性等来求函数的最值,从而解 决实际问题中的利润最大、用料最省等问题.
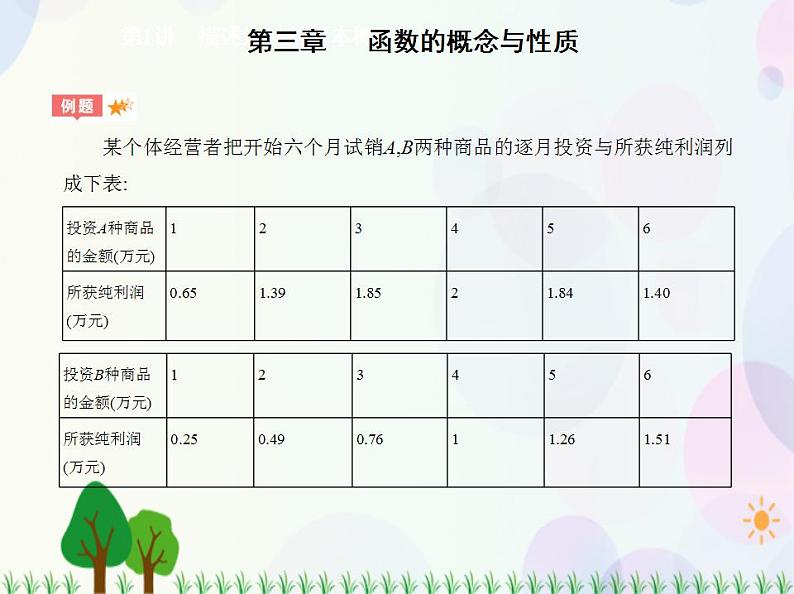
　　某个体经营者把开始六个月试销A,B两种商品的逐月投资与所获纯利润列 成下表:
　　该经营者准备下月投入12万元经营这两种商品,请你帮忙制订一个资金投入 方案,使该经营者获得最大纯利润,并按你的方案求出该经营者下月可获得的最 大纯利润(结果保留两位有效数字).
思路点拨利用已知数据画出散点图,根据散点图的形状选择函数模型,结合条件求出函数 的解析式及定义域,最后由函数的解析式解决相关问题.
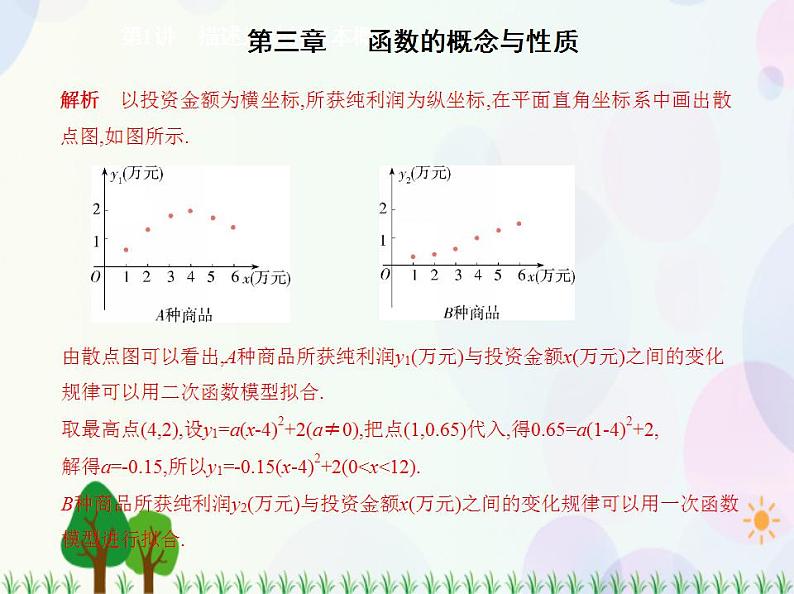
解析    以投资金额为横坐标,所获纯利润为纵坐标,在平面直角坐标系中画出散 点图,如图所示. 
由散点图可以看出,A种商品所获纯利润y1(万元)与投资金额x(万元)之间的变化规律可以用二次函数模型拟合.取最高点(4,2),设y1=a(x-4)2+2(a≠0),把点(1,0.65)代入,得0.65=a(1-4)2+2,解得a=-0.15,所以y1=-0.15(x-4)2+2(0