






数学24.2.3 圆心角、弧、弦、弦心距之间的关系习题课件ppt
展开旋转对称;圆心;圆心角
弧;弦;旋转对称;圆心角
1.圆是__________图形,旋转中心为________.顶点在圆心的角叫做________.
2.在同圆或等圆中,相等的圆心角所对的________相等,所对的________相等,所对弦的弦心距相等.其依据是圆的__________性,应用的前提是________相等.
3.推论:在同圆或等圆中,圆心角相等⇔弧相等⇔弦相等⇔弦心距相等.
1.下列命题中,正确的是( ) A.圆只有一条对称轴 B.圆有无数条对称轴,每条直径都是它的对称轴 C.圆是中心对称图形但不是旋转对称图形 D.圆既是中心对称图形又是旋转对称图形
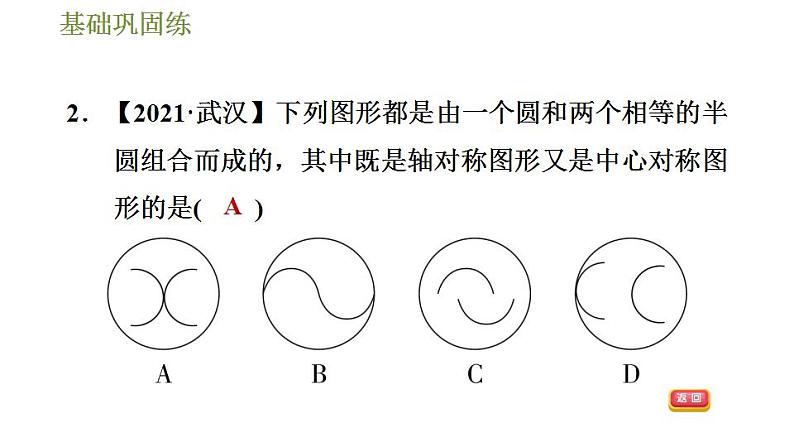
2.【2021·武汉】下列图形都是由一个圆和两个相等的半圆组合而成的,其中既是轴对称图形又是中心对称图形的是( )
3.如图,AB,CD分别为⊙O的两条弦,OM⊥AB于M,ON⊥CD于N,且∠AOB=∠COD,则( ) A.AB=CD B.OM=ON D.以上结论都正确
4.A,B,C,D四点在⊙O上,∠AOB=2∠COD,则下列关系正确的是( )
6.如图,AB是⊙O的直径,BC,CD,DA是⊙O的弦,且BC=CD=DA,则∠BCD的度数为( ) A.100° B.110° C.120° D.135°
9.【2021·安庆期末】如图,半径为5的⊙A中,弦BC,ED所对的圆心角分别是∠BAC,∠EAD.已知DE=6,∠BAC+∠EAD=180°,则弦BC的弦心距等于( )
10.如图,在⊙O中,直径AB平分弦CD,且交CD于点E,如果OE=BE,那么弦CD所对的圆心角是________度.
11.在⊙O中,M为弧AB的中点,则AB______2AM.(填“>”“<”或“=”)
A.AB+CD=EF B.AB+CD<EFC.AB+CD>EF D.无法确定
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.
证明:∵∠AOC=∠COD=60°,∴∠BOD=180°-(∠AOC+∠COD)=60°.∵OD=OB,∴△ODB为等边三角形.∴∠ODB=60°.∴∠ODB=∠COD.∴OC∥BD.
15.如图,在⊙O中,弦AD,BC相交于点E,连接OE,已知AD=BC,AD⊥CB.(1)求证:AB=CD;
(2)如果⊙O的半径为5,DE=1,求AE的长.
解:过点O作OF⊥AD于点F,作OG⊥BC于点G,连接OA,OC.则AF=FD,BG=CG.∵AD=BC,∴AF=CG.
(2)在(1)中,如果∠AOB=120°,其他条件不变,如图②所示,那么(1)中的结论还成立吗?若成立,请证明;若不成立,请说明理由.
数学九年级下册24.2.2 垂径定理习题课件ppt: 这是一份数学九年级下册24.2.2 垂径定理习题课件ppt,共21页。PPT课件主要包含了圆心角,弦心距,同圆或等圆等内容,欢迎下载使用。
初中数学沪科版九年级下册24.2.3 圆心角、弧、弦、弦心距之间的关系习题课件ppt: 这是一份初中数学沪科版九年级下册24.2.3 圆心角、弧、弦、弦心距之间的关系习题课件ppt,共21页。
初中数学沪科版九年级下册24.2.3 圆心角、弧、弦、弦心距之间的关系精品课件ppt: 这是一份初中数学沪科版九年级下册24.2.3 圆心角、弧、弦、弦心距之间的关系精品课件ppt,文件包含沪科版数学九年级下册242第3课时圆心角弧弦弦心距间关系ppt、沪科版数学九年级下册242第3课时圆心角弧弦弦心距间关系doc等2份课件配套教学资源,其中PPT共15页, 欢迎下载使用。













