人教版九年级上册第二十二章 二次函数综合与测试随堂练习题

这是一份人教版九年级上册第二十二章 二次函数综合与测试随堂练习题，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2021-2022学年度人教版九年级上册《二次函数》检测卷
一、选择题（每小题3分，共30分）
1.将抛物线y=3x2先向右平移2个单位,再向下平移1个单位后得到新的抛物线,则新抛物线对应的函数表达式是（   ）
A. y=3(x+2) 2+1                 B. y=3(x+2) 2 -1                 C. y=3(x-2) 2+1                 D. y=3(x-2) 2 -1
2.抛物线y=x2+4x+5是由抛物线y=x2+1经过某种平移得到，则这个平移可以表述为（   ）
A. 向左平移1个单位           B. 向左平移2个单位           C. 向右平移1个单位           D. 向右平移2个单位
3.如图，假设篱笆（虚线部分）的长度16m，则所围成矩形ABCD的最大面积是（   ）

A. 60m2                                  B. 63m2                                  C. 64m2                                  D. 66m2
4.将抛物线y=x2-2向上平移1个单位后所得新抛物线的表达式为(    )
A. y=x2-1                          B. y=x2-3                          C. y=(x+1)2-2                          D. y=(x-1)2-2
5.抛物线y=(x+2)2-3. 可以由抛物线y=x2. 平移得到，则下列平移过程正确的是（   ）

A. 先向左平移2个单位，再向上平移3个单位           B. 先向左平移2个单位，再向下平移3个单位
C. 先向右平移2个单位，再向下平移3个单位           D. 先向右平移2个单位，再向上平移3个单位
6.将抛物线y=﹣x2+1向上平移2个单位，得到的抛物线表达式为（   ）
A. y=﹣（x+2）2                   B. y=﹣（x﹣2）2                   C. y=﹣x2﹣1                   D. y=﹣x2+3
7.已知抛物线y=ax2+bx+c（b＞a＞0）与x轴最多有一个交点，现有以下四个结论：
①该抛物线的对称轴在y轴左侧；
②关于x的方程ax2+bx+c+2=0无实数根；
③a﹣b+c≥0；
④ a+b+cb−a 的最小值为3．
其中，正确结论的个数为（   ）
A. 1个                                       B. 2个                                       C. 3个                                       D. 4个
8.已知某二次函数的图象如图所示，则这个二次函数的解析式为（     ）

A. y=2(x+1)2+8           B. y=18(x+1)2−8           C. y=29(x−1)2+8           D. y=2(x−1)2−8
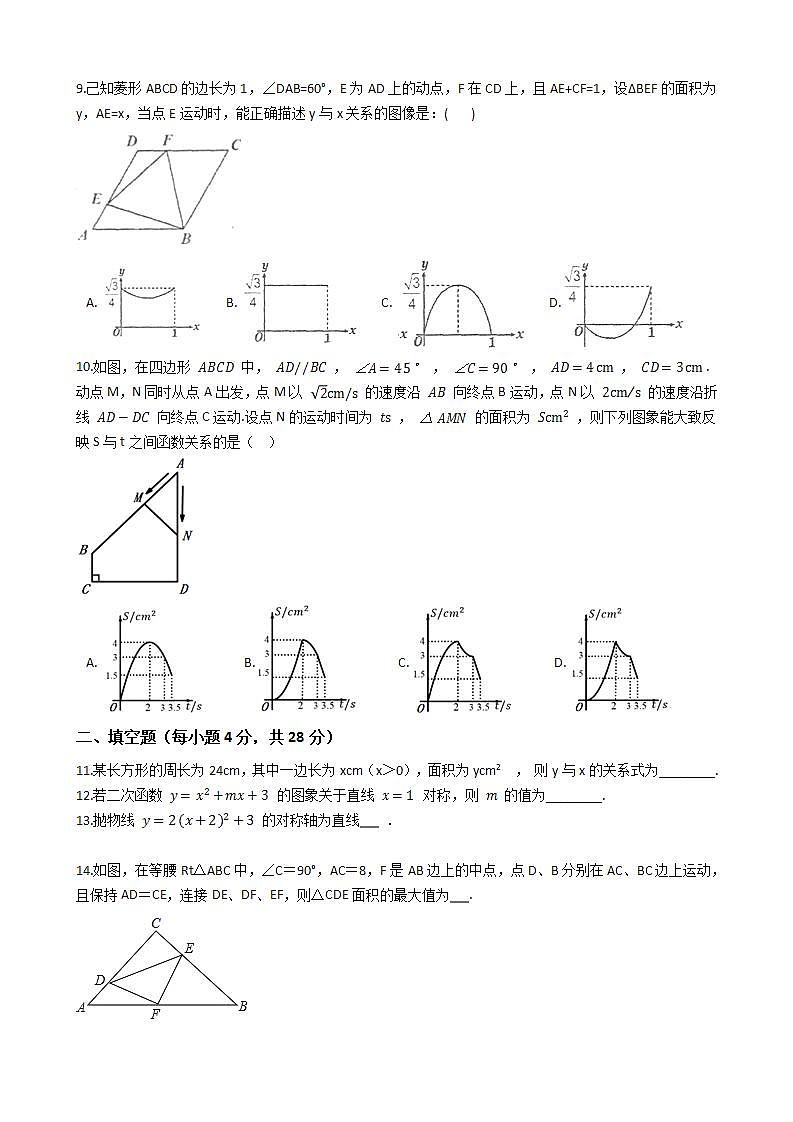
9.己知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE+CF=1，设ΔBEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是：(      )

A.        B.        C.        D. 
10.如图，在四边形 ABCD 中， AD//BC ， ∠A=45° ， ∠C=90° ， AD=4cm ， CD=3cm .动点M，N同时从点A出发，点M以 2cm/s 的速度沿 AB 向终点B运动，点N以 2cms 的速度沿折线 AD−DC 向终点C运动.设点N的运动时间为 ts ， △AMN 的面积为 Scm2 ，则下列图象能大致反映S与t之间函数关系的是（   ）

A.             B.             C.             D. 
二、填空题（每小题4分，共28分）
11.某长方形的周长为24cm，其中一边长为xcm（x＞0），面积为ycm2 ， 则y与x的关系式为________.
12.若二次函数 y=x2+mx+3 的图象关于直线 x=1 对称，则 m 的值为________.
13.抛物线 y=2(x+2)2+3 的对称轴为直线       ．

14.如图，在等腰Rt△ABC中，∠C＝90°，AC＝8，F是AB边上的中点，点D、B分别在AC、BC边上运动，且保持AD＝CE，连接DE、DF、EF，则△CDE面积的最大值为      .

15.矩形的周长为 20cm ，当矩形的长为       cm 时，面积有最大值是       cm2 ．

16.已知二次函数y＝﹣x2+x+6及一次函数y＝x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新图象（如图所示），当直线y＝x+m与这个新图象有四个交点时，m的取值范围是________.

17.阅读理解：
由所学一次函数知识可知，在平面直角坐标系内，一次函数y＝kx+b（k≠0）的图象与x轴交点横坐标，是一元一次方程kx+b＝0（k≠0）的解；在x轴下方的图象所对应的x的所有值是kx+b＜0（k≠0）的解集，在x轴上方的图象所对应的x的所有值是kx+b＞0（k≠0）的解集．例，如图1，一次函数kx+b＝0（k≠0）的图象与x轴交于点A（1，0），则可以得到关于x的一元一次方程kx+b＝0（k≠0）的解是x＝1；kx+b＜0（k≠0）的解集为x＜1．结合以上信息，利用函数图象解决下列问题：

（1）通过图1可以得到kx+b＞0（k≠0）的解集为________；
（2）通过图2可以得到
①关于x的一元二次方程ax2+bx+c＝0（a≠0）的解为________；
②关于x的不等式ax2+bx+c＞0（a≠0）的解集为________．
三、解答题（一）（每小题6分，共18分）
18.分别写出下列二次函数的对称轴和顶点坐标． 

（1）y=12(x+2)2−3 ；

（2）y=3x2−2x+1 ．
19.抛物线y=-x2+bx+c过点（0，-3）和（2，1），试确定抛物线的解析式，并求出抛物线与x轴的交点坐标．
20.已知抛物线的顶点坐标 (1,2) 且过点 (3,0) ，求该抛物线的解析式．
四、解答题（二）（每小题8分，共24分）

21.已知二次函数的图象以A（﹣1，4）为顶点，且过点B（2，﹣5）．

（1）求该函数的关系式；
（2）求该函数图象与坐标轴的交点坐标；
（3）将该函数图象向右平移，当图象经过原点时，A、B两点随图象移至A′、B′，求△OA′B′的面积．
22.如图，在平面直角坐标系中，抛物线y=ax2+3与y轴交于点A ， 过点A与x轴平行的直线交抛物线 y=13x2 于点B、C ， 求BC的长.

23.如图，在平面直角坐标系中，直线 y=x+2 与坐标轴交于 A，B 两点，点 A 在 x 轴上，点 B 在 y 轴上， C 点的坐标为 (1，0) ，抛物线 y=ax2+bx+c 经过点 A，B，C ．

（1）求抛物线的解析式；
（2）根据图象写出不等式 ax2+(b?1)x+c>2 的解集；
（3）点 P 是抛物线上的一动点，过点 P 作直线 AB 的垂线段，垂足为 Q 点,当 PQ=22 时，求P点的坐标．
五、解答题（三）（每小题10分，共20分）

24.如图，在平面直角坐标系中，将抛物线y=33x2先向右平移1个单位，再向下平移433个单位，得到新的抛物线y=ax2+bx+c，该抛物线与y轴交于点B，与x轴正半轴交于点C．

（1）求点B和点C的坐标；
（2）如图1，有一条与y轴重合的直线l向右匀速平移，移动的速度为每秒1个单位，移动的时间为t秒，直线l与抛物线y=ax2+bx+c交于点P，当点P在x轴上方时，求出使△PBC的面积为23的t值；
（3）如图2，将直线BC绕点B逆时针旋转，与x轴交于点M（1，0），与抛物线y=ax2+bx+c交于点A，在y轴上有一点D（0，233），在x轴上另取两点E，F（点E在点F的左侧），EF=2，线段EF在x轴上平移，当四边形ADEF的周长最小时，先简单描述如何确定此时点E的位置？再直接写出点E的坐标．

25.如图，已知在平面直角坐标系中，四边形ABCO是梯形，且BC∥AO，其中A（6，0），B（3，3），∠AOC=60°，动点P从点O以每秒2个单位的速度向点A运动，动点Q也同时从点B沿B→C→O的线路以每秒1个单位的速度向点O运动，当点P到达A点时，点Q也随之停止，设点P，Q运动的时间为t（秒）．

（1）求点C的坐标及梯形ABCO的面积；
（2）当点Q在CO边上运动时，求△OPQ的面积S与运动时间t的函数关系式，并写出自变量t的取值范围；
（3）以O，P，Q为顶点的三角形能构成直角三角形吗？若能，请求出t的值；若不能，请说明理由．


答案解析部分
一、选择题（每小题3分，共30分）
1.【答案】 D
【解析】【解答】解：将抛物线y=3x2先向右平移2个单位,再向下平移1个单位后得到: y=3(x-2) 2 -1.
故答案为：D.
【分析】根据平移口诀“左加右减自变量，上加下减常数项”可得出答案.
2.【答案】 B
【解析】【解答】∵原抛物线的顶点为（0，1），新抛物线的顶点为（-2，1），
∴是抛物线y= x2+1 向左平移2个单位得到，故答案为：B．
【分析】利用配方法将原抛物线配成顶点式，得出顶点坐标，同时根据元抛物线的解析式得出原抛物线的顶点坐标，通过观察两顶点的坐标，根据点的平移的坐标变化规律即可得出答案。
3.【答案】 C
【解析】【解答】解：设BC=xm，则AB=（16﹣x）m，矩形ABCD面积为ym2 ，
根据题意得：y=（16﹣x）x=﹣x2+16x=﹣（x﹣8）2+64，
当x=8m时，ymax=64m2 ，
则所围成矩形ABCD的最大面积是64m2 ．
故选C．
【分析】设BC=xm，表示出AB，矩形面积为ym2 ， 表示出y与x的关系式，利用二次函数性质求出面积最大值即可．
4.【答案】 A
【解析】【解答】解：将抛物线y=x2-2向上平移1个单位后所得新抛物线的表达式为x2-2+1=x2-1.
故答案为：A.
【分析】根据二次函数图像的平移规律：上加下减，左加右减，将抛物线y=ax2向上或向下平移m个单位，再向左或向右平移n个单位即得到y=a（x±n）2±m。根据平移规则即可得出平移后的抛物线的解析式。
5.【答案】 B
【解析】【解答】解：∵抛物线y=(x+2)2-3. 可以由抛物线y=x2. 平移得到
∴先向左平移2个单位，再向下平移3个单位。
故答案为：B
【分析】直接根据抛物线的平移法则（上加下减，左加右减），解答即可。
6.【答案】 D
【解析】【解答】解：将抛物线y=﹣x2+1向上平移2个单位，得到的抛物线表达式为y=﹣x2+1+2=﹣x2+3，
故选：D．
【分析】根据左加右减，上加下减可得函数解析式y=﹣x2+1+2，再整理即可．
7.【答案】 D
【解析】【解答】解：∵b＞a＞0
∴﹣ b2a ＜0，
所以①正确；
∵抛物线与x轴最多有一个交点，
∴b2﹣4ac≤0，
∴关于x的方程ax2+bx+c+2=0中，△=b2﹣4a（c+2）=b2﹣4ac﹣8a＜0，
所以②正确；
∵a＞0及抛物线与x轴最多有一个交点，
∴x取任何值时，y≥0
∴当x=﹣1时，a﹣b+c≥0；
所以③正确；
当x=﹣2时，4a﹣2b+c≥0
a+b+c≥3b﹣3a
a+b+c≥3（b﹣a）
a+b+cb−a ≥3
所以④正确．
故选：D．
【分析】从抛物线与x轴最多一个交点及b＞a＞0，可以推断抛物线最小值最小为0，对称轴在y轴左侧，并得到b2﹣4ac≤0，从而得到①②为正确；由x=﹣1及x=﹣2时y都大于或等于零可以得到③④正确．
8.【答案】 D
【解析】【解答】解：由图知道，抛物线的顶点坐标是（1，-8）
故二次函数的解析式为y=2（x-1）2-8
故答案为：D．
【分析】顶点式：y=a（x-h）2+k（a，h，k是常数，a≠0），其中（h，k）为顶点坐标．
9.【答案】 A
【解析】【解答】解：过点E作EM⊥AB，EN⊥DC，垂足为M、N，过点B作BG⊥DC，垂足为G．

∵AE=DF=x，
∴DE=FC=a-x．
∵∠A=∠NDE=∠C=60°，
∴EM= 32  x，NE= 32 （1-x），BG= 32 ,
∵△EFB的面积=菱形的面积-△AEB的面积-△DFE的面积-△FCB的面积，
∴y= 32×1−12×1×32x−12×x×32(1−x)−12×(1−x)×32  
= 34x2−34x+34  
当x=0或x=1时，S△EFB有最大值；
故答案为：A。
【分析】过点E作EM⊥AB，EN⊥DC，垂足为M、N，过点B作BG⊥DC，垂足为G．由菱形的性质可将EM、NE用含x的代数式表示出来，用勾股定理可求得BG的长，根据△EFB的面积=菱形的面积-△AEB的面积-△DFE的面积-△FCB的面积即可写出y与x之间的函数关系式，由题意知，当x=0或x=1时，函数有最大值，由此即可判断正确的图像。
10.【答案】 B
【解析】【解答】解: ∠A=45°，CD=3cm，
AB= 32+32 = 32 cm,
∴M由A到B需3秒,N由A到D需2秒,到C需3.5秒,
下面分三种情况讨论:
( 1 )当N在AD上时,即0＜t≤2,如图1,

作ME⊥AD于E,
可知AN=2t,AM= 2t ,
∴EM=t,
∴ s=12AN⋅ME=12×2t⋅t=t2
故此段图像是一条开口向上的抛物线;
( 2 ) 当N在CD上且M没到达B时,即2＜t＜3,如图2,

作MF⊥CD于F,延长AB与DC的延长线交于O,
可知DN=2t-4,AM= 2t ,OD=4,OA= 42 ,
∴ON=4-DN=8-2t,OM= 42−2t ,
∴MF=4- t,
∴ sΔOAD=12OD⋅AD=12×4×4=8 ,
sΔNAD=12ND⋅AD=12×(2t−4)×4=4t−8 ,
sΔOMN=12ON⋅MF=12×(8−2t)⋅(4−t)=(4−t)2 ,
∴ s=8−(4t−8)−(4−t)2=−t2+4t ,
故此段图像是一条开口向下的抛物线;
( 3 )当N在CD上且M与B重合时,即3≤t≤3.5,如图3,

可知BC=1,DN=2t-4,
∴CN=3-DN=7-2t ,
∴ sABCD=12(BC+AD)⋅CD=12×5×3=152 ,
sΔNAD=12ND⋅AD=12×(2t−4)×4=4t−8 ,
sΔBCN=12BC⋅CN=12×1×(7−2t)=72−t ,
∴ s=152−(4t−8)−(72−t)=12−3t ,
故此段图像是一条呈下降趋势的线段;
综上所述,答案是B.
【分析】先求出AB= 32 cm，可知M由A到B需3秒,N由A到D需2秒,到C需3.5秒.分三种情况讨论:(1)当N在AD上时,即0＜t≤2,画出图形求解; (2) 当N在CD上且M没到达B时,即2＜t＜3, 画出图形求解; (3)当N在CD上且M与B重合时,即3≤t≤3.5, 画出图形求解.即可选出正确答案.
二、填空题（每小题4分，共28分）
11.【答案】 y=(12−x)⋅x
【解析】【解答】根据长方形的周长和面积公式可知：y＝x(12－x)＝12x－x2
故答案为：y＝12x－x2

【分析】根据长方形的周长及一边长，先求出另一边长为（12-x）,利用长方形的面积=长×宽，即可求出 y与x的关系式 .
12.【答案】 -2
【解析】【解答】解：∵二次函数 y=x2+mx+3 的图象关于直线 x=1 对称，
∴ −m2=1
解得，m=-2，
故答案为：-2.
【分析】由二次函数的对称轴公式x=−b2a ， 其中a、b分别叫二次项系数、一次项系数即可所得答案.
13.【答案】 x=-2
【解析】【解答】由y=2(x−2)²+3可知，抛物线的顶点坐标为(2,3)，
∴抛物线对称轴为直线x=2.故答案为：x=-2.
【分析】由抛物线的顶点式得到抛物线的顶点坐标为(2，3)，得到抛物线对称轴为直线.
14.【答案】 8
【解析】【解答】解：设AD＝x，则CE＝AD＝x，CD＝8﹣x，
∵∠C＝90°，
∴S△CDE＝ 12CE⋅CD ＝ 12x(8−x) ＝﹣ 12 （x2﹣8x＋16﹣16）＝﹣ 12 （x﹣4）2＋8，
∵﹣ 12 ＜0，
∴当x＝4，即AD＝4时，△CDE面积有最大值是8，
故答案为：8.
【分析】设AD＝x，则CE＝AD＝x，CD＝8﹣x，根据三角形面积公式建立出s与x的函数关系式，由二次函数性质可得最大值.
15.【答案】 5；25
【解析】【解答】设矩形的长为xcm，则矩形的宽为(10-x)cm，则矩形的面积y=x(10-x)=-x2+10x(0＜x＜10)
函数开口向下，当x=5时，函数有最大值，最大值y=-52+10×5=25，
故当矩形的长为5cm时，面积有最大值是25 cm2 ．
故答案为：5,25
【分析】根据矩形的周长可得出矩形的长与宽的和为10，设矩形的长为xcm，表示出矩形的宽，再根据矩形的面积公式，列出矩形的面积y与x的函数解析式，然后将其转化为顶点式，利用二次函数的性质，可求得结果。
16.【答案】 ﹣7＜m＜﹣3
【解析】【解答】解：如图所示，过点B作直线y＝x+m1 ， 将直线向下平移到恰在点C处相切，
则一次函数y＝x+m在两条直线之间时，两个图象有4个交点，
 
令y＝﹣x2+x+6＝0，解得：x＝﹣2或3，即点B坐标（3，0），
翻折抛物线的表达式为：y＝（x﹣3）（x+2）＝x2﹣x﹣6（﹣2≤x≤3）,
将一次函数与二次函数表达式联立并整理得：x2﹣2x﹣6﹣m＝0，
△＝b2﹣4ac＝4+4（6+m）＝0，解得：m＝﹣7，
当一次函数过点B时，将点B坐标代入：y＝x+m得：0＝3+m，解得：m＝﹣3，
所以当直线y＝x+m与这个新图象有四个交点时，m的取值范围是﹣7＜m＜﹣3.
【分析】如图所示，过点B作直线y＝x+m1 ， 将直线向下平移到恰在点C处相切，
则一次函数y＝x+m在两条直线之间时，两个图象有4个交点，根据抛物线与x轴交点的坐标特点即可求出带你B的坐标，根据翻折的性质得出翻折抛物线的表达式为：y＝（x﹣3）（x+2）＝x2﹣x﹣6（﹣2≤x≤3）,然后联立翻折后的解析式与一次函数的解析式得出x2﹣2x﹣6﹣m＝0，根据两函数只有一个交点得出其根的判别式的值为0，从而列出方程，求解得出m的值，然后将点B的坐标代入一次函数的解析式求出m的值，综上所述即可得出答案.
17.【答案】 （1）x > 1
（2）x1＝﹣1，x2＝2；x < ﹣1或x > 2
【解析】【解答】解：（1）通过图1可以得到kx+b > 0（k≠0）的解集为x > 1；（2）通过图2可以得到①关于x的一元二次方程ax2+bx+c＝0（a≠0）的解为x1＝﹣1，x2＝2；②关于x的不等式ax2+bx+c > 0（a≠0）的解集为x < ﹣1或x > 2．
故答案为：x＞1；x1＝﹣1，x2＝2；x < ﹣1或x > 2．
【分析】（1）直接根据图象即可得出答案；（2）①直接根据抛物线与x轴的交点即可得出答案；②直接根据图象即可得出答案．
三、解答题（一）（每小题6分，共18分）
18.【答案】 （1）解： ∵ y=12(x+2)2−3 ，
∴二次函数的对称轴为 x=−2 ，顶点坐标为 (−2, −3)

（2）解： ∵ y=3x2−2x+1=3(x−13)2+23 ，
∴二次函数的对称轴为 x=13 ，顶点坐标为 (13, 23)
【解析】【分析】（1）利用函数解析式直接写出对称轴及顶点坐标。
（2）先利用配方法将函数解析式转化为顶点式，再写出对称轴及顶点坐标。
四、解答题
19.【答案】 解：∵抛物线y=-x2+bx+c过点（0，-3）和（2，1），
∴ {c=−3−4+2b+c=1 ，解得 {b=4c=−3 ，
抛物线的解析式为y=-x2+4x-3，
令y=0，得-x2+4x-3=0，即x2-4x+3=0，
∴x1=1，x2=3，
∴抛物线与x轴的交点坐标为（1，0）、（3，0）
【解析】【分析】运用待定系数法将两点坐标分别代入y=-x2+bx+c，得到关于b、c的方程组，解方程组可求出b、c的值。将 y=0代入求得的解析式中，得一个一元二次方程，解方程所求的未知数的值即是交点横坐标
20.【答案】 解：由题意，设 y=a(x−1)2+2 ，
∵抛物线过点（3，0），
∴ a(3−1)2+2=0 ，
解得 a=−12 ，
∴ y=−12(x−1)2+2
即 y=−12x2+x+32 .
【解析】【分析】由于已知抛物线的顶点坐标，则可设顶点式y=a（x-1）2+2，然后把（3，0）代入求出a即可．
四、解答题（二）（每小题8分，共24分）

21.【答案】 解：（1）由顶点A（﹣1，4），可设函数关系式为y=a（x+1）2+4（a≠0），

将点B（2，﹣5）代入解析式得：﹣5=a（2+1）2+4，
解得：a=﹣1．
则二次函数的关系式为：y=﹣（x+1）2+4=﹣x2﹣2x+3；
（2）令x=0，
得y=﹣（0+1）2+4=3，
故图象与y轴交点坐标为（0，3）．
令y=0，
得0=﹣（x+1）2+4，
解得x1=﹣3，x2=1．
故图象与x轴交点坐标为（﹣3，0）和（1，0）；
（3）设抛物线与x轴的交点为M、N（M在N的左侧），
由（2）知：M（﹣3，0），N（1，0）
当函数图象向右平移经过原点时，M与O重合，因此抛物线向右平移了3个单位
故A'（2，4），B'（5，﹣5）
∴S△OA′B′=12×（2+5）×9﹣12×2×4﹣12×5×5=15．

【解析】【分析】（1）设函数关系式为y=a（x+1）2+4（a≠0），将点B坐标代入解析式，求出a的值即可求得函数关系式；

（2）分别令x=0，y=0，即可求得函数与y轴、x轴的交点坐标；
（3）由（2）可知：抛物线与x轴的交点分别在原点两侧，由此可求出当抛物线与x轴负半轴的交点平移到原点时，抛物线平移的单位，由此可求出A′、B′的坐标．由于△OA′B′不规则，可用面积割补法求出△OA′B′的面积．
22.【答案】 解：BC=6
【解析】【解答】解：当x=0时，y=0+3=3
∴点A（0,3）
又∵BC∥x轴
∴点B、C的纵坐标都是3
∴13x2=3
解，得  x=±3
∴B（-3,3），C（3,3）
∴BC=3-（-3）=6.
【分析】先求出抛物线y=ax2+3与y轴的交点A的坐标是（0,3），则B、C的纵坐标都是-3，将y=-3代入y=13x2求出B、C的坐标，进而可求线段BC的值。
23.【答案】 （1）解：当 y=0 时， x+2=0 ，解得 x=?2 ，
当 x=0 时， y=0+2=2 ，
则点 A(?2,0) ，点 B(0,2) ，
把 A(?2,0) ， B(0,2) ， C(1,0) ，分别代入 y=ax2+bx+c 得
{4a?2b+c=0a+b+c=0c=2 解得： a=?1 ， b=?1 ， c=2 ，
∴该抛物线的解析式为 y=?x2?x+2

（2）解：由不等式 ax2+(b?1)x+c>2 ，
得 ax2+bx+c>x+2 ，
由图像可知，二次函数图像在一次函数图像上方，
则不等式 ax2+(b?1)x+c>2 的解集为 ?2