沪科版九年级下册24.3.2 圆内接四边形习题ppt课件

这是一份沪科版九年级下册24.3.2 圆内接四边形习题ppt课件，共25页。PPT课件主要包含了答案显示，核心必知，见习题，答案C等内容，欢迎下载使用。

半圆或直径所对的圆周角是________；90°的圆周角所对的弦是直径．
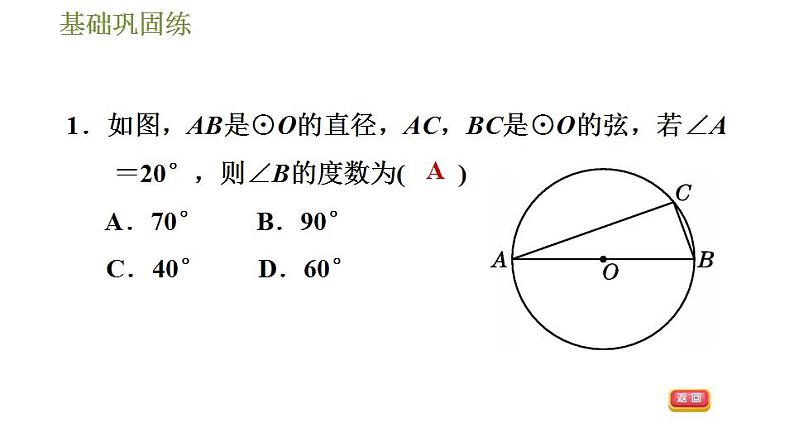
1．如图，AB是⊙O的直径，AC，BC是⊙O的弦，若∠A＝20°，则∠B的度数为(　　) A．70° B．90° C．40° D．60°
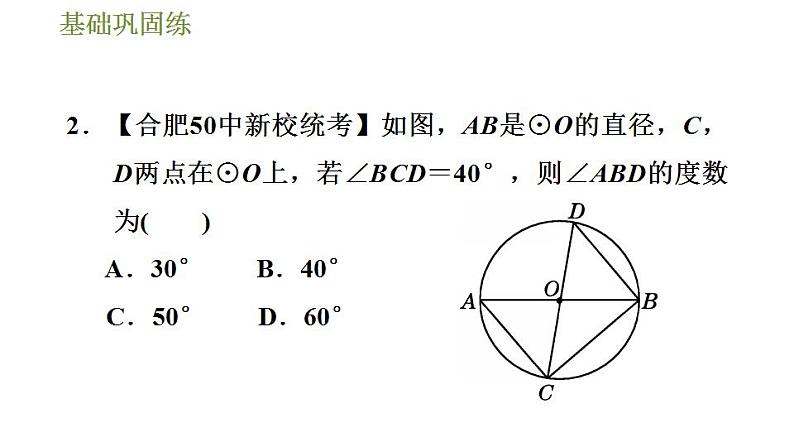
2．【合肥50中新校统考】如图，AB是⊙O的直径，C，D两点在⊙O上，若∠BCD＝40°，则∠ABD的度数为(　　) A．30° B．40° C．50° D．60°
【点拨】∵AB是⊙O的直径，∴∠ACB＝90°.∵∠BCD＝40°，∴∠ACD＝90°－∠BCD＝50°，∴∠ABD＝∠ACD＝50°.
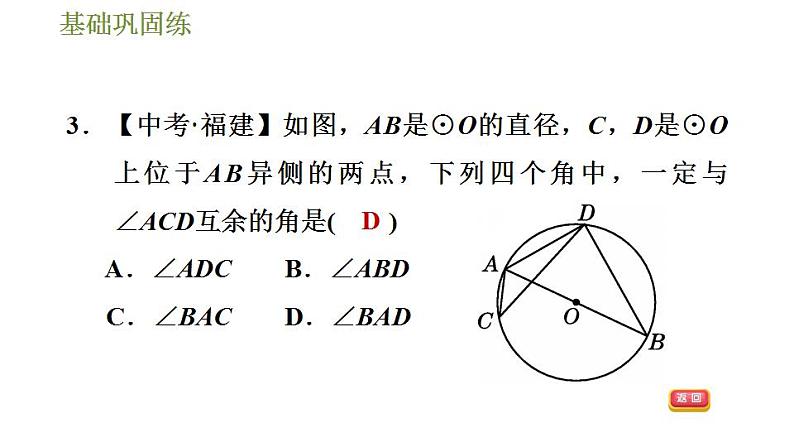
3．【中考·福建】如图，AB是⊙O的直径，C，D是⊙O上位于AB异侧的两点，下列四个角中，一定与∠ACD互余的角是(　　) A．∠ADC B．∠ABD C．∠BAC D．∠BAD
A．25° B．50° C．40° D．80°
5．如图，点P在以AB为直径的半圆形内，连接AP，BP并延长分别交半圆于点C，D，连接AD，BC并延长交于点F，作直线PF，下列说法一定正确的是(　　)①AC垂直平分BF；②AC平分∠BAF；③FP⊥AB；④BD⊥AF. A．①③ B．①④ C．②④ D．③④
6．【中考·常州】如图，把直角三角尺的直角顶点O放在破损玻璃镜的圆周上，两直角边与圆弧分别交于点M，N，量得OM＝8 cm，ON＝6 cm，则该玻璃镜的半径是(　　)
7．下列直角三角尺与圆弧的位置关系中，可判断圆弧为半圆的是(　　)
8．下列结论正确的是(　　) A．直径所对的角是直角 B．90°的圆心角所对的弦是直径 C．同一条弦所对的圆周角相等 D．半圆所对的圆周角是直角
9．如图，点A，B，C，D都在⊙O上，AB＝AD，BA，CD的延长线交于点E，且AB＝AE，求证：BC是⊙O的直径．
证明：如图，连接BD.∵AE＝AD＝AB，∴∠E＝∠ADE，∠ADB＝∠ABD.∵∠E＋∠EDB＋∠ABD＝180°，∴2∠EDA＋2∠ADB＝180°，∴∠EDA＋∠ADB＝90°，∴∠BDC＝∠EDB＝90°，∴BC是⊙O的直径．
10．【2021·安庆月考】如图，Rt△ABC中，AB⊥BC，AB＝12，BC＝8，P是△ABC内部的一个动点，且满足∠PAB＝∠PBC，连接PC，求线段CP长的最小值．
11．【中考·安顺】如图，半径为3的⊙A经过原点O和点C(0，2)，B是y轴左侧⊙A优弧上一点，则tan ∠OBC为(　　)
12.如图，在锐角三角形ABC中，AB＞AC，AD⊥BC于点D，以AD为直径的⊙O分别交AB，AC于点E，F，连接DE，DF.(1)求证：∠EAF＋∠EDF＝180°；
证明：∵AD是⊙O的直径，∴∠AED＝∠AFD＝90°.∵∠AED＋∠AFD＋∠EAF＋∠EDF＝360°，∴∠EAF＋∠EDF＝180°.
(2)已知P是射线DC上一个动点，当点P运动到PD＝BD时，连接AP，交⊙O于点G，连接DG.设∠EDG＝α，∠APB＝β，那么α与β有何数量关系？试证明你的结论(在探究α与β的数量关系时，可直接运用(1)的结论进行推理与解答)．
解：α＝2β.证明：∵DP＝BD，AD⊥BC，∴AB＝AP.∴∠B＝∠APB＝β.由(1)的结论可知，∠BAP＋∠EDG＝180°.∵∠BAP＋∠B＋∠APB＝180°，∴∠BAP＝180°－2β.∴180°－2β＋α＝180°. ∴α＝2β.
13．【合肥瑶海区模拟】如图，△ABC内接于⊙O，已知AB＝c，BC＝a，AC＝b，⊙O的半径为R.