高中数学4.4.2 对数函数应用举例教案配套课件ppt

这是一份高中数学4.4.2 对数函数应用举例教案配套课件ppt，共19页。PPT课件主要包含了学习目标，前提诊测，对数的定义，关于直线yx对称，对数函数的引入，Y2x，Xlog2y，变化过程，Ylog2x，对数函数的定义等内容，欢迎下载使用。

1、理解对数函数的概念；
2、掌握对数函数的图象和性质；
3、数形结合意识的继续加强。
重点是对数函数的图象和性质；
难点是对数函数与指数函数的联系。
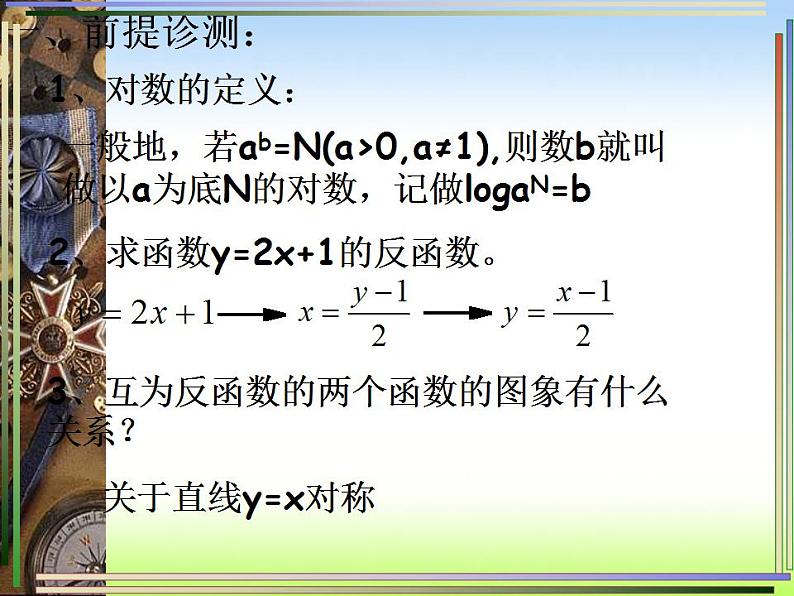
2、求函数y=2x+1的反函数。
3、互为反函数的两个函数的图象有什么关系？
一般地，若ab=N(a>0,a≠1),则数b就叫做以a为底N的对数，记做lgaN=b
问题1：某种细胞分裂时，由1个分裂为2个，2个分裂为4个……1个这样的细胞分裂x次后，得到的细胞个数设为y,则y与x的函数关系式为：
问题2：某种细胞分裂时，由1个分裂为2个，2个分裂为4个……如果要求这种细胞经过多少次分裂，大约可以得到1万个，10万个……细胞，那么分裂次数x就是要得到的细胞个数y的函数。由对数的定义，这个函数可以写成：
结论：函数y=lg2x和指数函数y=2x互为反函数
函数y=lgax（a>0,a≠1）叫做对数函数
①对数函数y=lgax和指数函数y=ax互为反函数
②对数函数的解析式可由指数函数求反函数得到
③对数函数的定义域、值域也就是指数函数的 值域、定义域
想一想：对数函数的定义域和值域分别是什么？
因为指数函数的定义域是R 值域是（0，+∞）所以对数函数的定义域是（0，+∞） 值域是R
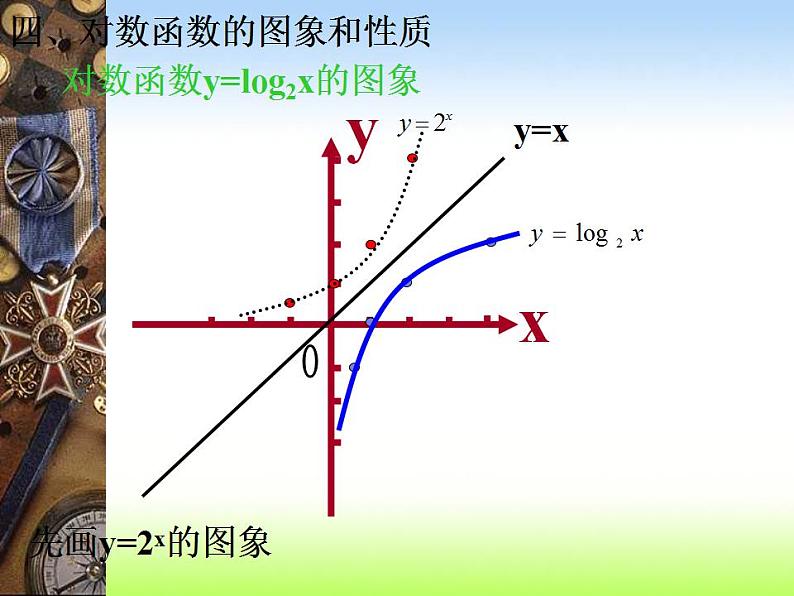
四、对数函数的图象和性质
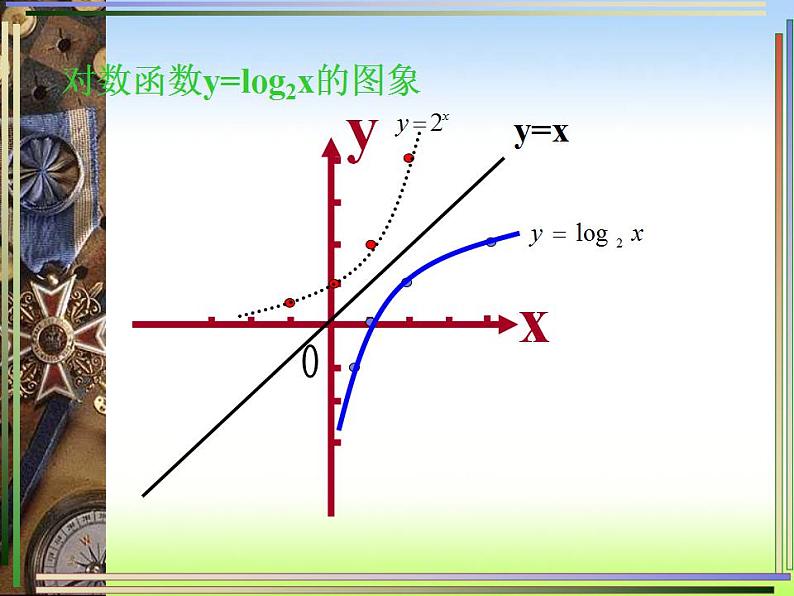
对数函数y=lg2x的图象
y=lgax（a>1）的图象
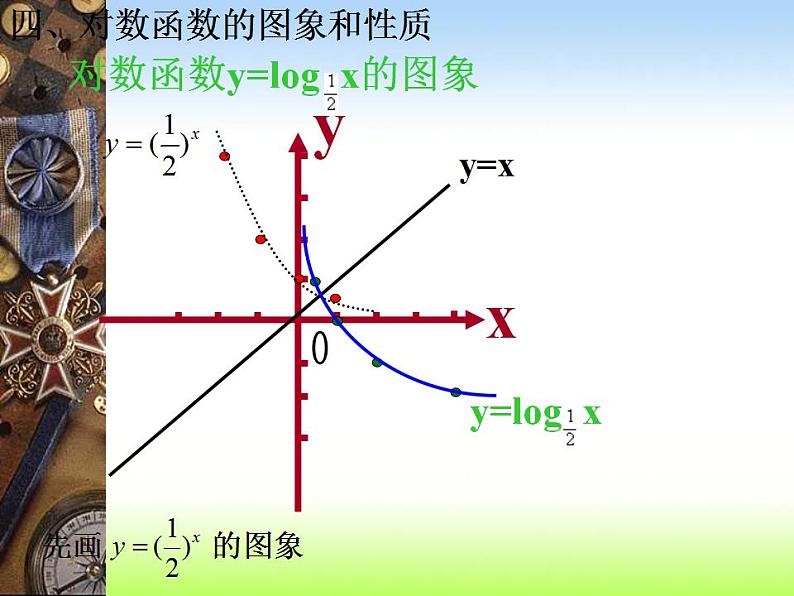
y=lgax（0一般地，对数函数y=lgax在a>1及0过点（1，0），即x=1时y=0
在（0，+∞）上是增函数
在（0，+∞）上是减函数
当0＜x＜1时，y＜0当x=1时，y=0当x＞1时，y＞0
当0＜x＜1时，y＞0当x=1时，y=0当x＞1时，y＜0
例1：求下列函数的定义域：①y=lgax2 ②y=lga(4-x) ③y=lga(9-x2)
分析：此题主要利用对数函数y=lgax的定义域为（0，+∞）求解。
①因为x2 >0,即x≠0， 所以函数y=lgax2 的定义域是{x│x≠0}
②因为4-x>0,即x<4, 所以函数y=lga(4-x)的定义域是{x│x<4}
③因为9-x2>0,即-3相同性质：都位于y轴右方，都经过点（1，0），这说明这两个函数的定义域都是（0，+∞），且x=1时y=0
2、求下列函数的定义域：
通过本节课的学习，大家应逐步掌握对数函数的图象和性质，并能利用对数函数的性质解决一些简单问题，如求对数形式的复合函数的定义域问题。
1预习内容： 预习提纲：①同底数的两个对数如何比较大小？ ②不同底数的两个对数如何比较大小？2挑战自己： 你能否尽可能完整地总结出指数函数和对数函数的区别和联系？请试一试。