江苏省镇江市丹徒区2021-2022学年八年级上学期第一次月考数学【试卷+答案】

第一次月作业八年级数学

一、单选题(每小题3分，共18分）

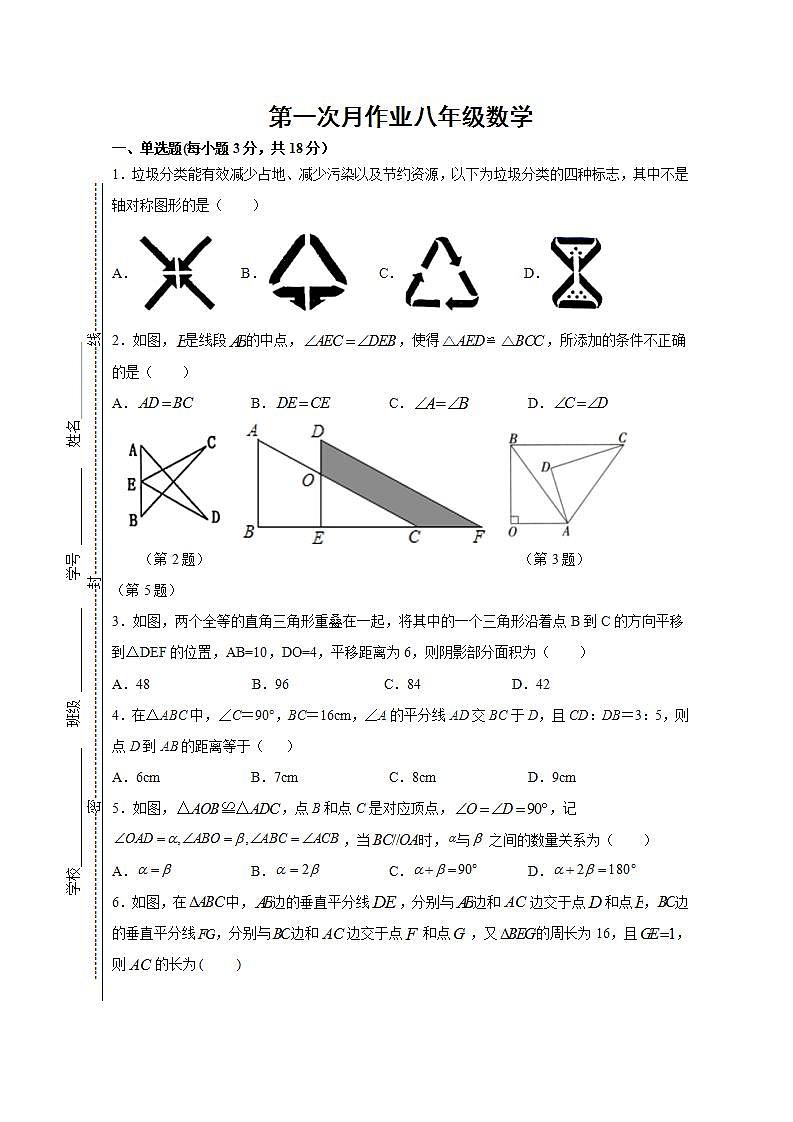
1．垃圾分类能有效减少占地、减少污染以及节约资源，以下为垃圾分类的四种标志，其中不是轴对称图形的是（　　）

A．   B．    C．      D．

2．如图，是线段的中点，，使得，所添加的条件不正确的是（    ）

A． B． C． D．

（第2题）             （第3题）                      （第5题）

3．如图，两个全等的直角三角形重叠在一起，将其中的一个三角形沿着点B到C的方向平移到△DEF的位置，AB=10，DO=4，平移距离为6，则阴影部分面积为（　　）

A．48                             B．96                           C．84                          D．42

4．在△ABC中，∠C＝90°，BC＝16cm，∠A的平分线AD交BC于D，且CD：DB＝3：5，则点D到AB的距离等于（   ）

A．6cm B．7cm C．8cm D．9cm

5．如图，，点B和点C是对应顶点，，记，当时，与之间的数量关系为（    ）

A． B． C． D．

6．如图，在中，边的垂直平分线，分别与边和边交于点和点，边的垂直平分线，分别与边和边交于点和点，又的周长为16，且，则的长为　　

          A．16      B．15      C．14      D．13

二、填空题(每小题2分，共24分）

7．小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第____块去，这利用了三角形全等中的____原理．

（第7题）                  （第8题）                      （第9题）

8．如图，在方格纸中，以为一边作，使与全等，，，，四个点中符合条件的点的个数为_________．

9．如图所示，，，，，，则的度数是______．

10．如图所示的网格是正方形网格，图形的各个顶点均为格点，则∠1+∠2=_____．

（第10题）             （第11题）                   （第12题）

11．如图，在Rt△ABC中，∠ACB=90°，点D在边AB上，将△CBD沿CD折叠，使点B恰好落在边AC上的点E处．若∠A=24°，则∠CDE=________°．

12．如图，AB⊥CD，且AB=CD，E，F是AD上两点，CF⊥AD，BE⊥AD．若CF=8，BE=6，AD=10，则EF的长为__________________．

13．在4×4的方格中有五个同样大小的正方形（阴影）如图摆放，移动标号为①的正方形到空白方格中，使其与其余四个正方形组成的新图形是一个轴对称图形，这样的移法有______种．

14．如图，A．B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有______个．

（第13题）           （第14题）             （第15题）

15．如图，AD垂直平分BC于点D， EF垂直平分AB于点F，点E在AC上，BE+CE=20cm，则AB=______．

16．在中，，，是的中线，设长为，则的取值范围是______．

17．如图，已知△ABC的面积为18，BP平分∠ABC，且AP⊥BP于点P，则△BPC的面积是_____．

（第17题）                              （第18题）

18．如图，在锐角中，，边上有一定点分别是和边上的动点，当的周长最小时，的度数是_________．

三、解答题(共78分）

19．(本题8分）用尺规作图法作的角平分线．（请填空，图上保留作图痕迹即可）

已知：．

求作：的角平分线．

作法：

（1）以    为圆心，适当长为半径画弧，交于点，交于点．

（2）分别以点　   为圆心，　　 为半径画弧，两弧在的内部交于点．

（3）画射线，射线即为所求．

20．(本题8分）如图，网格中的与为轴对称图形，且顶点都在格点上．

（1）利用网格，作出与的对称轴；

（2）结合图形，在对称轴上画出一点，使得最小；

（3）如果每个小正方形的边长为1，请直接写出的面积．

21．(本题8分）如图，AC和BD相交于点O，OA=OC，OB=OD．

（1）求证：∠A=∠C；

（2）求证：AB∥CD．

22．(本题8分）如图，在四边形ABCD中，AB∥CD，∠1＝∠2，AD＝EC．

（1）求证：△ABD≌△EDC；

（2）若AB＝2，BE＝3，求CD的长．

23．(本题8分）如图，已知Rt△ABC≌Rt△ADE，∠ABC＝∠ADE＝90°，BC与DE相交于点F，连接AF．

（1）求证：DF＝BF；

（2）连接CE，求证直线AF是线段CE的垂直平分线．

24．(本题8分）如图，AD∥BC，AE平分∠BAD，BE平分∠ABC，AF＝AD，AB＝AD+BC．

（1）AE与BE垂直吗？说明你的理由；

（2）若AE＝5，BE＝3，试求出四边形ABCD的面积．

25．(本题10分）如图，如图，在△ABC中，AB＜AC，边的垂直平分线交的外角的平分线于点，垂足为E，DF⊥AC于点F，于点，连接CD．

(1)求证：BG＝CF；

(2)若AB＝10cm，AC＝14cm，求AG的长．

26．(本题10分）如图（1），AB＝4cm，AC⊥AB，BD⊥AB，AC＝BD＝3cm．点P在线段AB上以1cm/s的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动．它们运动的时间为t（s）．

（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；

（2）如图（2），将图（1）中的“AC⊥AB，BD⊥AB”为改“∠CAB＝∠DBA＝60°”，其他条件不变．设点Q的运动速度为xcm/s，是否存在实数x，使得△ACP与△BPQ全等？若存在，求出相应的x、t的值；若不存在，请说明理由．

27．(本题10分）定义：如图，为直线同侧的两点，过点作直线的对称点，连接交直线于点，连接，则称点为点关于直线的“等角点”．

如图①，在中，分别是上的点，，然后将绕点顺时针旋转一定角度，连接，得到图②，延长交的延长线于点，延长至点，使，连接，得到图③，请解答下列问题：

（1）在图②中，与的数量关系是          ；

（2）在图③中，求证：点为点，关于直线的“等角点”．

2021-2022年八年级第一学期第一次数学月作业参考答案

一、单选题

1．C   2．A   3．A   4．A   5．B   6．C

二、填空题

7．4    ASA    8．3   9．58°   10．45°   11．69°    12．4

13．3   14．9   15．20cm．   16．   17．9   18．80°

三、解答题

19．（1）；（2）、；大于的长．...........................3分

（2）作图，...........................5分

20．（1）略；...........................3分（2）略；...........................3分（3）3；..........................2分

21．

（1）证明：∵OA=OC，OB=OD，∠AOB=∠COD，

∴△AOB≌△COD． ...........................4分

∴∠A=∠C；...........................6分

（2） ∵∠A=∠C，∴AB∥CD．...........................8分

22．

（1）证明：∵AB∥CD，∴∠ABD＝∠EDC．在△ABD和△EDC中，，

∴△ABD≌△EDC（AAS），..........................4分

（2）∵△ABD≌△EDC，∴AB＝DE＝2，BD＝CD，∴CD＝BD＝DE+BE＝2+3＝5．..........8分

23．

解：证明：（1）∵Rt△ABC≌Rt△ADE，∴AB=AD，在Rt△ADF与Rt△ABF中，，∴Rt△ADF≌Rt△ABF（HL），∴DF=BF；...........................4分

（2）连接CE，∵Rt△ABC≌Rt△ADE，∴BC=DF，AC=AE，∵DF=BF，∴FC=FE，∴点A和点F在CE的中垂线上，∴AF是CE的中垂线．..........................8分

24．

解：（1）结论：AE⊥BE．理由：∵AD∥BC，∴∠BAD+∠ABC＝180°，又∵AE平分∠BAD，BE平分∠ABC，∴∠DAE＝∠EAF＝∠BAD，∠ABE＝∠CBE＝∠ABC，

∴∠EAB+∠EBA＝（∠BAD+∠ABC）＝×180°＝90°，∵∠EAB+∠ABE+∠AEB＝180°，∴∠AEB＝90°，∴AE⊥BE；...........................4分

（2）∵AF＝AD，AB＝AD+BC，∴BF＝BC，在△AED和△AEF中，，∴△AED≌△AEF（SAS），∴S四边形ADEF＝2S△AEF，同理△BEF≌△BEC，∴S四边形BCEF＝2S△BEF，

∴S四边形ABCD＝S四边形ADEF+S四边形BCEF＝2S△AEF+2S△BEF＝2S△ABE＝2××5×3＝15．.........................8分

25．

（1）证明：如图所示，连接DB，

AD是△ABC的外角平分线，DG⊥AB，DF⊥CA，DF=DG，DE垂直平分BC，DC=DB，在Rt△CDF与Rt△BDG中， Rt△CDF≌Rt△BDG (HL) BG=CF．...........................4分

（2）解：GAD=FAD，AGD=AFD，AD=AD，在△ADG与△ADF中

△ADG≌△ADF(AAS)，...........................8分

AG=AF，BG=CF，，

AG=(AC-AB)= (14-10)=2 (cm) ．...........................10分

26．

解：（1）当时，，，又，在和中，

．，．，即线段与线段垂直．...........................5分

（2）①若，则，，则，解得：；

②若，则，，则，解得：；

综上所述，存在或使得与全等．...........................10分

27．

解：（1）BD=CE；...........................3分

（2）由“等角点”的定义可知：如图，点A和点A′关于直线l对称，∴∠APC=∠A′PC，

∵∠A′PC=∠BPD，∴∠APC=∠BPD，

可得若满足∠APC=∠BPD，则点P为点A，B关于直线l的“等角点”，

如图③，由（1）知△BAD≌△CAE，∴∠ABD=∠ACE，BD=CE，∵DM=EN，∴BM=CN，

在△ABM和△ACN中，，∴△ABM≌△ACN（SAS），
∴∠BAM=∠CAN，即∠BAC+∠CAM=∠CAM+∠MAN，∴∠MAN=∠BAC，

∴点A为点C，M关于直线BN的“等角点”．...........................10分