苏科版八年级上册第一章 全等三角形综合与测试课时练习

这是一份苏科版八年级上册第一章 全等三角形综合与测试课时练习，共13页。试卷主要包含了下列说法正确的是，完成下列推理过程等内容，欢迎下载使用。
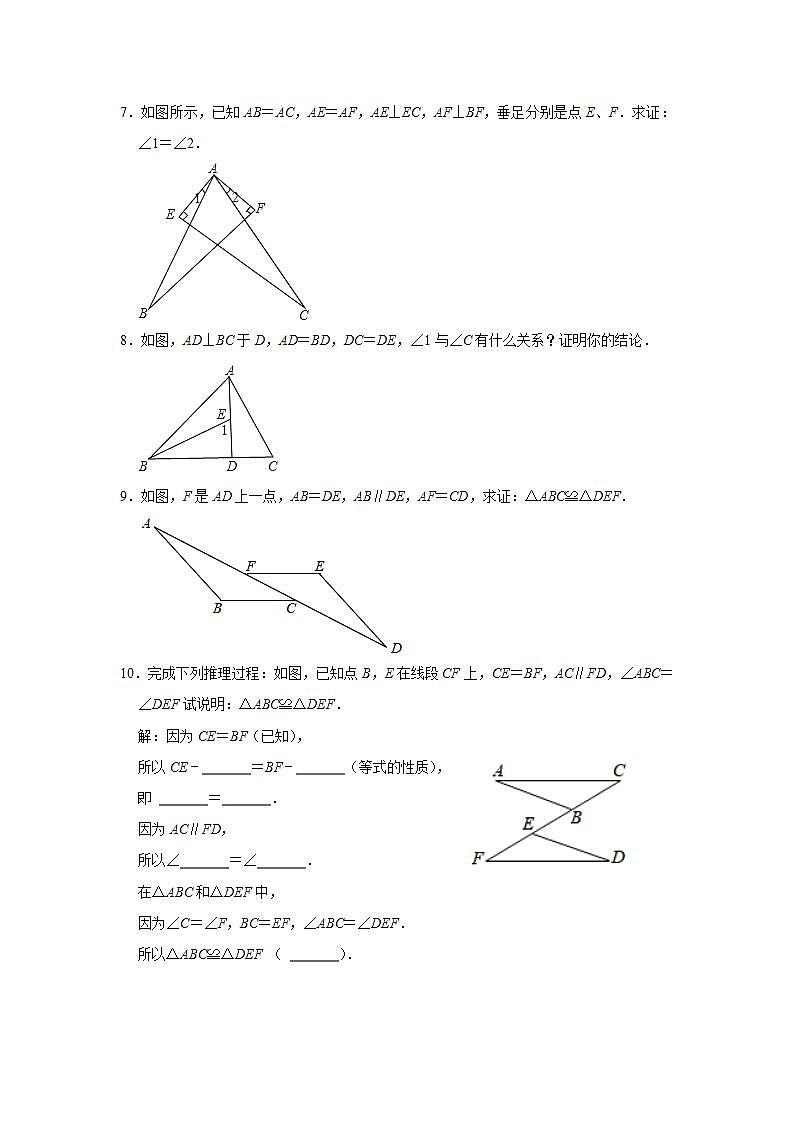
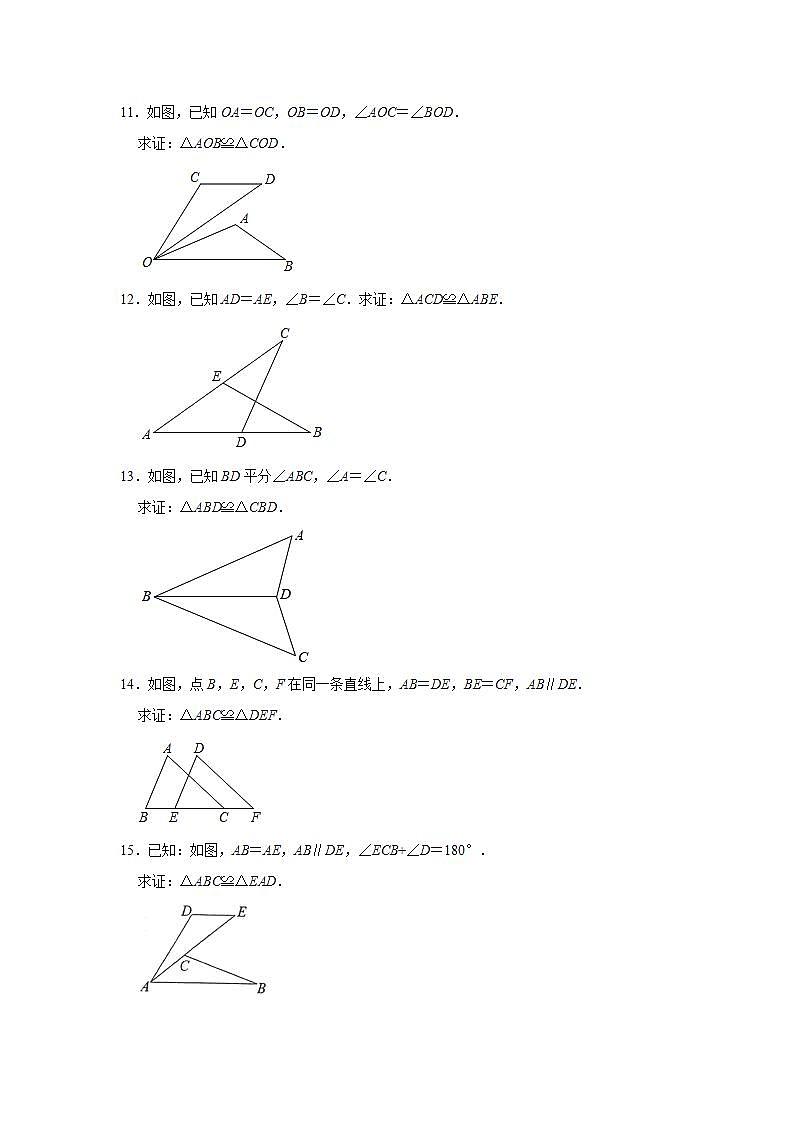
2021-2022年苏科版八年级数学上册《第1章全等三角形》单元能力提升训练（附答案）1．已知图中的两个三角形全等，则∠α的度数是（　　）A．72° B．60° C．58° D．50°2．如图，红红书上的三角形被墨迹污染了一部分，她根据所学的知识很快就画了一个与书上完全一样的三角形，那么红红画图的依据是（　　）A．SSS B．SAS C．ASA D．AAS3．下列说法正确的是（　　）A．全等三角形是指形状相同的两个三角形 B．全等三角形的周长和面积分别相等C．全等三角形是指面积相等的两个三角形     D．所有的等边三角形都是全等三角形4．如图，△ABC≌△EDF，DF＝BC，AB＝ED，AF＝20，EC＝10，则AE的长是　 　．5．如图，△ABC≌△DCB，∠DBC＝40°，则∠AOB＝　   　°．6．如图，BE⊥AC于点D，且AD＝CD，BD＝ED，若∠ABC＝54°，则∠E＝　   　°． 7．如图所示，已知AB＝AC，AE＝AF，AE⊥EC，AF⊥BF，垂足分别是点E、F．求证：∠1＝∠2．8．如图，AD⊥BC于D，AD＝BD，DC＝DE，∠1与∠C有什么关系？证明你的结论．9．如图，F是AD上一点，AB＝DE，AB∥DE，AF＝CD，求证：△ABC≌△DEF．10．完成下列推理过程：如图，已知点B，E在线段CF上，CE＝BF，AC∥FD，∠ABC＝∠DEF试说明：△ABC≌△DEF．解：因为CE＝BF（已知），所以CE﹣　   　＝BF﹣　   　（等式的性质），即 　   　＝　   　．因为AC∥FD，所以∠　   　＝∠　   　．在△ABC和△DEF中，因为∠C＝∠F，BC＝EF，∠ABC＝∠DEF．所以△ABC≌△DEF （ 　   　）．  11．如图，已知OA＝OC，OB＝OD，∠AOC＝∠BOD．求证：△AOB≌△COD．12．如图，已知AD＝AE，∠B＝∠C．求证：△ACD≌△ABE．13．如图，已知BD平分∠ABC，∠A＝∠C．求证：△ABD≌△CBD．14．如图，点B，E，C，F在同一条直线上，AB＝DE，BE＝CF，AB∥DE．求证：△ABC≌△DEF．15．已知：如图，AB＝AE，AB∥DE，∠ECB+∠D＝180°．求证：△ABC≌△EAD． 16．如图，已知∠ABC＝∠BAD，∠C＝∠D，求证：△ABC≌△BAD．17．已知：如图，AC＝BD，∠1＝∠2．求证：△ADB≌△BCA．18．已知：如图，OA＝OD，OB＝OC．求证：△OAB≌△ODC．19．如图，已知点B，C，F，E在同一直线上，∠1＝∠2，BF＝CE，AB∥DE．求证：△ABC≌△DEF．20．如图，AB＝CB，BE＝BF，∠1＝∠2，证明：△ABE≌△CBF．    21．如图，点D在AB上，点E在AC上，BE与CD相交于点O，AB＝AC，AD＝AE．求证：△BDC≌△CEB．22．已知，如图，点D，E分别在AB，AC上，∠B＝∠C，AB＝AC．求证：△AEB≌△ADC．23．如图，AC＝AE，∠1＝∠2，AB＝AD．求证：△ABC≌△ADE．24．如图，已知△ABC为等边三角形，D为BC延长线上的一点，CE平分∠ACD，CE＝BD，求证：（1）△ABD≌△ACE；（2）试判断△ADE的形状，并证明．
参考答案1．解：∵图中的两个三角形全等a与a，c与c分别是对应边，那么它们的夹角就是对应角∴∠α＝50°故选：D．2．解：根据题意，三角形的两角和它们的夹边是完整的，所以可以利用“角边角”定理作出完全一样的三角形．故选：C．3．解：A、全等三角形的形状相同，但形状相同的两个三角形不一定是全等三角形．故该选项错误；B、全等三角形是指能够完全重合的两个三角形，则全等三角形的周长和面积一定相等，故B正确；C、全等三角形面积相等，但面积相等的两个三角形不一定是全等三角形．故该选项错误；D、两个等边三角形，形状相同，但不一定能完全重合，不一定全等．故错误．故选：B．4．解：∵△ABC≌△EDF，∴AC＝EF，∴AC﹣CE＝EF﹣CE，即AE＝CF，∵AF＝20，EC＝10，∴AE＝×（20﹣10）＝5．故答案为：5．5．解：∵△ABC≌△DCB，∠DBC＝40°，∴∠ACB＝∠DBC＝40°，∴∠AOB＝∠ACB+∠DBC＝40°+40°＝80°．故答案为：80．6．解：∵BE⊥AC，AD＝CD，∴AB＝CB，即△ABC为等腰三角形，∴BD平分∠ABC，即∠ABE＝∠CBE＝∠ABC＝27°，在△ABD和△CED中，，∴△ABD≌△CED（SAS），∴∠E＝∠ABE＝27°，故答案为：277．证明：∵AE⊥EC，AF⊥BF，∴△AEC是Rt△，△AFB是Rt△，在Rt△AEC与Rt△AFB中，，∴Rt△AEC≌Rt△AFB（HL），∴∠EAC＝∠FAB，∴∠EAC﹣∠BAC＝∠FAB﹣∠BAC，即∠1＝∠2．8．解：∠C＝∠1，理由如下：∵AD⊥BC，∴∠ADC＝∠BDE＝90°．又∵DC＝DE，AD＝BD，∴△ADC≌△BDE．∴∠C＝∠1．9．证明：∵AB∥DE，∴∠A＝∠D，∵AF＝DC，∴AF+FC＝DC+FC，即AC＝DF，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．10．解：因为CE＝BF（已知），所以CE﹣BE＝BF﹣BE（等式的性质），即CB＝FE．因为AC∥FD，所以∠C＝∠F．在△ABC和△DEF中，因为∠C＝∠F，BC＝EF，∠ABC＝∠DEF．所以△ABC≌△DEF （ASA）．故答案为BE，BE；CB，FE；C，F；ASA．11．证明：∵∠AOC＝∠BOD，∴∠AOC﹣∠AOD＝∠BOD﹣∠AOD，即∠COD＝∠AOB，在△AOB和△COD中，，∴△AOB≌△COD（SAS）．12．证明：在△ACD和△ABE中，，∴△ACD≌△ABE（AAS）．13．证明：∵BD平分∠ABC，∴∠ABD＝∠CBD，在△ABD与△CBD中，，∴△ABD≌△CBD（AAS）．14．证明：∵BE＝CF，∴BE+EC＝CF+EC，即BC＝EF，又∵AB∥DE，∴∠B＝∠1，在△ABC和△DEF中，，∴△ABC≌△DEF（SAS）．15．证明：∵AB∥DE，∴∠CAB＝∠E，∵∠ECB+∠D＝180°，∠ECB+∠ACB＝180°，∴∠D＝∠ACB，在△ABC与△EAD中，，∴△ABC≌△EAD（AAS）．16．证明：在△ABC和△BAD中，，∴△ABC≌△BAD（AAS）．17．证明：在△ADB和△BCA中，，∴△ADB≌△BCA（SAS）．18．证明：在△OAB和△ODC中，∴△OAB≌△ODC（SAS）．19．证明：∵BF＝CE，∴BF﹣FC＝CE﹣CF，即BC＝EF，∵AB∥DE，∴∠E＝∠B，在△ABC和△DEF中，，∴△ABC≌△DEF（ASA）．20．证明：∵∠1＝∠2，∴∠1+∠FBE＝∠2+∠FBE，即∠ABE＝∠CBF，在△ABE与△CBF中，，∴△ABE≌△CBF（SAS）．21．证明：∵AB＝AC，∴∠DBC＝∠ECB，∵AB＝AC，AD＝AE，∴BD＝CE，在△BDC和△CEB中，，∴△BDC≌△CEB（SAS）．22．证明：在△AEB和△ADC中，，∴△AEB≌△ADC（ASA）．23．证明：∵∠1＝∠2，∴∠BAC＝∠DAE，在△BAC和△DAE中，，∴△BAC≌△DAE（SAS），24．（1）证明：∵△ABC为等边三角形，∴∠B＝∠ACB＝60°，AB＝AC，∴∠ACD＝120°，∵CE平分∠ACD，∴∠ACE＝∠DCE＝60°，∴∠B＝∠ACE，在△ABD和△ACE中，，∴△ABD≌△ACE（SAS）；（2）解：△ADE是等边三角形，证明如下：由（1）得：△ABD≌△ACE，∴AD＝AE，∠BAD＝∠CAE，即∠BAC+∠CAD＝∠DAE+∠CAD，∴∠DAE＝∠BAC＝60°，∴△ADE为等边三角形．