






高中数学人教A版 (2019)必修 第一册第五章 三角函数5.2 三角函数的概念示范课课件ppt
展开“物以类聚,人以群分”,之所以“分群”、“分类”,是因为同类之间有很多共同点,彼此紧密地联系.我们现在研究的三角函数,同角的正弦、余弦、正切之间有什么关系呢?
同角三角函数的基本关系式1.公式(1)平方关系: . (2)商数关系: . 2.公式推导如图,以正弦线MP、余弦线OM和半径OP的长作为直角三角形三边长,而且OP=1.
对同角三角函数基本关系式的理解
变形公式的应用要注意哪些方面?
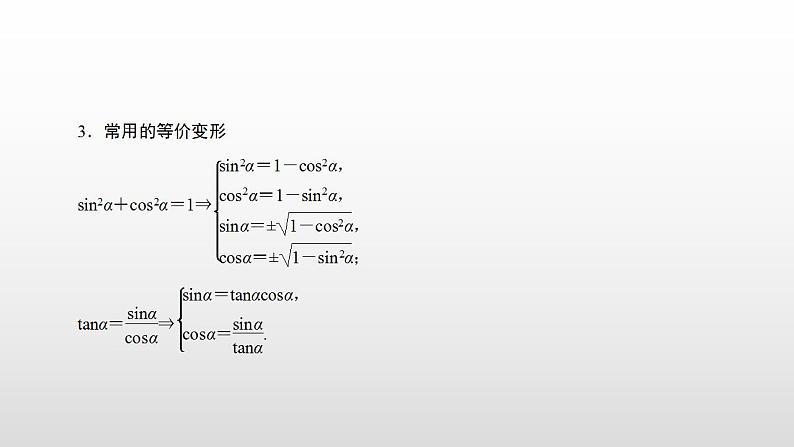
(1)使用变形公式sinα=± ,csα=± 时,“±”号是由α的终边所在的象限确定的,而对于其他形式的变形公式就不必考虑符号问题.(2)对这些关系式不仅要牢牢掌握,还要能灵活运用(正用、逆用、变形应用).
命题方向1 ⇨根据同角三角函数关系求值
在使用开平方关系sinα=± 和csα=± 时,一定要注意正负号的选取,确定正负号的依据是角α所在的象限,如果角α所在的象限是已知的,则按三角函数在各个象限的符号来确定正负号;如果角α所在的象限是未知的,则需要按象限进行讨论.
命题方向2 ⇨弦化切求值
命题方向3 ⇨化简三角函数式
[思路分析] (1)把二次根式中的被开方式化为完全平方式.(2)中所含角α的三角函数次数相对较高,且分子、分母含常数“1”.解答本题中的(1),(2)时应充分利用“sin2α+cs2α=1”这一条件.
三角函数式的化简过程中常用的方法:(1)化切为弦,即把非正弦、非余弦的函数都化成正弦、余弦函数,从而减少函数名称,达到化简的目的.(2)对于含有根号的,常把根号下式子化成完全平方式,然后去根号,达到化简的目的.(3)对于化简含高次的三角函数式,往往借助于因式分解,或构造sin2α+cs2α=1,以降低函数次数,达到化简的目的.
命题方向4 ⇨三角恒等式的证明
利用同角三角函数的基本关系证明三角恒等式三角恒等式的证明方法非常多,其主要方法有:(1)从左向右推导或从右向左推导,一般由繁到简;(2)左右归一,即证明左右两边都等于同一个式子;(3)化异为同法,即针对题设与结论间的差异,有针对地变形,以消除差异;(4)变更命题法,如要证明 ,可证ad=bc;(5)比较法,即设法证明“左边-右边=0”或“ =1”.
sinθ±csθ,sinθ·csθ三者的关系及方程思想的运用
sinθ±csθ,sinθ·csθ三者的关系:(1)对于三角函数式sinθ±csθ,sinθ·csθ之间的关系,可以通过(sinθ±csθ) =1±2sinθ·csθ进行转化.(2)若已知sinθ±csθ,sinθ·csθ中三者之一,利用方程思想进一步可以求得sinθ,csθ的值,从而求出其余的三角函数值.
注意:要注意题目中的隐含条件
人教A版 (2019)必修 第一册5.2 三角函数的概念课文ppt课件: 这是一份人教A版 (2019)必修 第一册5.2 三角函数的概念课文ppt课件,共19页。PPT课件主要包含了复习回顾,三角函数的定义,Pxy,与角α终边相同的角等内容,欢迎下载使用。
人教A版 (2019)必修 第一册5.2 三角函数的概念教课课件ppt: 这是一份人教A版 (2019)必修 第一册5.2 三角函数的概念教课课件ppt,共21页。PPT课件主要包含了新知初探·课前预习,tanα,α的正切,答案A,答案D,题型探究·课堂解透等内容,欢迎下载使用。
数学必修 第一册5.2 三角函数的概念多媒体教学ppt课件: 这是一份数学必修 第一册5.2 三角函数的概念多媒体教学ppt课件,文件包含522pptx、522DOC等2份课件配套教学资源,其中PPT共38页, 欢迎下载使用。













