高中人教版新课标A1.3 空间几何体的表面积与体积课后作业题

1．3．2　球的体积和表面积

A级　基础巩固

一、选择题

1．如果三个球的半径之比是1∶2∶3，那么最大球的表面积是其余两个球的表面积之和的 (　B　)

A．倍　　 B．倍　　

C．2倍　　 D．3倍

[解析]　设小球半径为1，则大球的表面积S大＝36π，S小＋S中＝20π，＝．

2．若两球的体积之和是12π，经过两球球心的截面圆周长之和为6π，则两球的半径之差为 (　A　)

A．1  B．2

C．3  D．4

[解析]　设两球的半径分别为R，r(R>r)，则由题意得，解得．故R－r＝1．

3．一个正方体表面积与一个球表面积相等，那么它们的体积比是 (　A　)

A．  B．

C．  D．

[解析]　由6a2＝4πR2得＝，∴＝＝()3＝．

4．球的表面积与它的内接正方体的表面积之比是 (　C　)

A．  B．

C．  D．π

[解析]　设正方体的棱长为a，球半径为R，则3a2＝4R2，∴a2＝R2

球的表面积S1＝4πR2，正方体的表面积 S2＝6a2＝6×R2＝8R2，∴S1∶S2＝．

5．正方体的内切球与其外接球的体积之比为 (　C　)

A．1∶  B．1∶3

C．1∶3  D．1∶9

[解析]　设正方体的棱长为a，则它的内切球的半径为a，它的外接球的半径为a，故所求体积之比为1∶3．

6．若与球外切的圆台的上、下底面半径分别为r，R，则球的表面积为 (　C　)

A．4π(r＋R)2  B．4πr2R2

C．4πRr  D．π(R＋r)2

[解析]　解法一：如图，设球的半径为r1，则在Rt△CDE中，DE＝2r1，CE＝R－r，DC＝R＋r．由勾股定理得4r＝(R＋r)2－(R－r)2，解得r1＝．故球的表面积为D球＝4πr＝4πRr．

解法二：如图，设球心为O，球的半径为r1，连接OA，OB，则在Rt△AOB中，OF是斜边AB上的高．由相似三角形的性质得OF2＝BF·AF＝Rr，即r＝Rr，故r1＝，故球的表面积为S球＝4πRr．

二、填空题

7．已知一个正方体的所有顶点在一个球面上，若这个正方体的表面积为18，则这个球的体积为____．

[解析]　设正方体的棱长为a，则6a2＝18

∴a＝．

设球的半径为R，则由题意知2R＝＝3

∴R＝．

故球的体积V＝πR3＝π×()3＝．

8．已知两个球的表面积之比为1∶16，则这两个球的半径之比为__1∶4__．

[解析]　球的表面积公式为4πR2，设两球半径分别为r1，r2

∴＝，∴＝．

三、解答题

9．体积相等的正方体、球、等边圆柱(轴截面为正方形)的全面积分别是S1，S2，S3，试比较它们的大小．

[解析]　设正方体的棱长为a，球的半径为R，等边圆柱的底面半径为r，则S1＝6a2，S2＝4πR2，S3＝6πr2．

由题意知，πR3＝a3＝πr2·2r

∴R＝a，r＝a

∴S2＝4π(a)2＝4π·a2＝a2

S3＝6π(a)2＝6π·a2＝a2

∴S2<S3．

又6a2>3a2＝a2

即S1>S3．

∴S1，S2，S3的大小关系是S2<S3<S1．

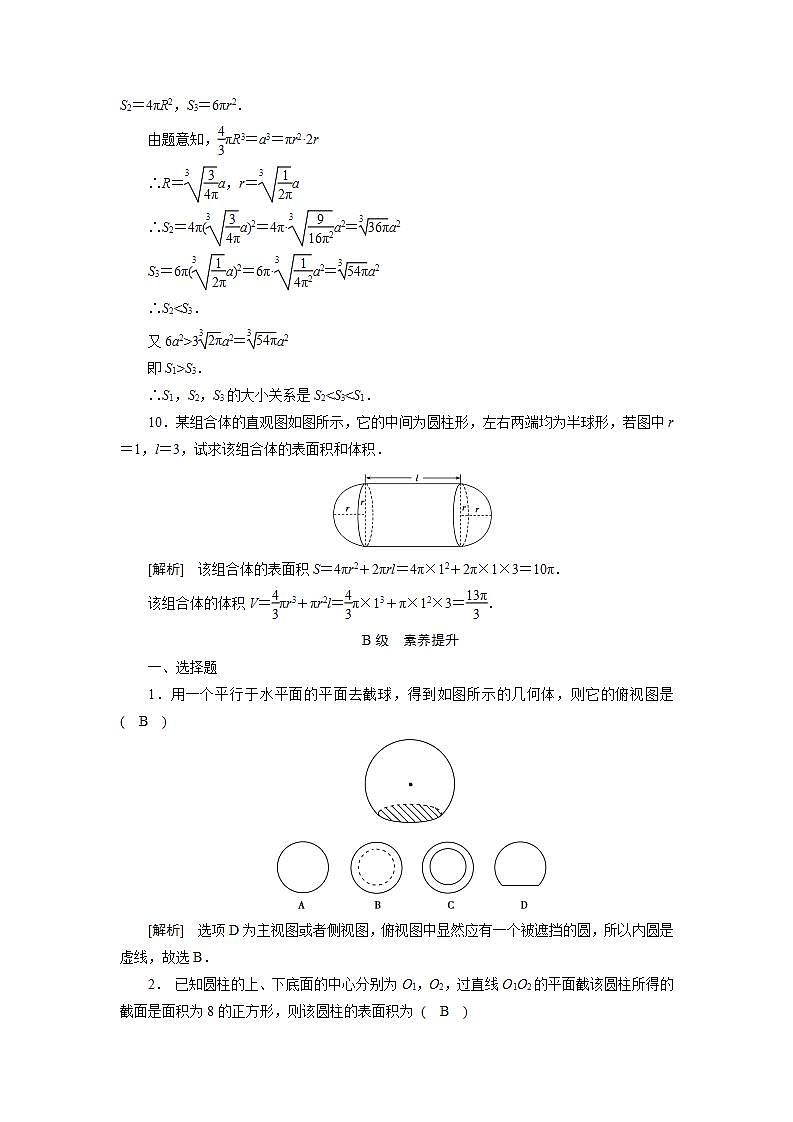
10．某组合体的直观图如图所示，它的中间为圆柱形，左右两端均为半球形，若图中r＝1，l＝3，试求该组合体的表面积和体积．

[解析]　该组合体的表面积S＝4πr2＋2πrl＝4π×12＋2π×1×3＝10π．

该组合体的体积V＝πr3＋πr2l＝π×13＋π×12×3＝．

B级　素养提升

一、选择题

1．用一个平行于水平面的平面去截球，得到如图所示的几何体，则它的俯视图是 (　B　)

[解析]　选项D为主视图或者侧视图，俯视图中显然应有一个被遮挡的圆，所以内圆是虚线，故选B．

2． 已知圆柱的上、下底面的中心分别为O1，O2，过直线O1O2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为 (　B　)

A．12π  B．12π

C．8π  D．10π

[解析]　根据题意，可得截面是边长为2的正方形，

结合圆柱的特征，可知该圆柱的底面为半径是的圆，且高为2，所以其表面积为S＝2π()2＋2π··2＝12π，故选B．

3．一个球与一个上、下底面为正三角形，侧面为矩形的棱柱的三个侧面和两个底面都相切，已知这个球的体积为，那么这个正三棱柱的体积是 (　D　)

A．96  B．16

C．24  D．48

[解析]　由题意可知正三棱柱的高等于球的直径，从棱柱中间截得球的大圆内切于正三角形，正三角形与棱柱底的三角形全等，设三角形边长为a，球半径为r，由V球＝×πr3＝解r＝2．S底＝×a×＝a·r×3，得a＝2r＝4，所以V柱＝S底·2r＝48．

4．已知某几何体的三视图如图所示，其中正视图、侧视图均是由三角形与半圆构成，俯视图由圆与内接三角形构成，根据图中的数据可得此几何体的体积为 (　C　)

A．＋  B．＋

C．＋  D．＋

[解析]　由已知的三视图可知原几何体的上方是三棱锥，下方是半球，∴V＝×(×1×1)×1＋[×()3]×＝＋，故选C．

二、填空题

5．一个半径为2的球体经过切割后，剩余部分几何体的三视图如图所示，则该几何体的表面积为__16π__．

[解析]　该几何体是从一个球体中挖去个球体后剩余的部分，所以该几何体的表面积为×(4π×22)＋2×＝16π．

6．已知正方体ABCD－A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M(如图)，则四棱锥M－EFGH的体积为____．

[解析]　由题意可得，底面四边形EFGH为边长为的正方形，其面积SEFGH＝()2＝，顶点M到底面四边形EFGH的距离为d＝

由四棱锥的体积公式可得：VM－EFGH＝××＝．

C级　能力拔高

1．盛有水的圆柱形容器的内壁底面半径为5 cm，两个直径为5 cm的玻璃小球都浸没于水中，若取出这两个小球，则水面将下降多少？

[解析]　设取出小球后，容器中水面下降h cm，

两个小球的体积为V球＝2[×()3]＝(cm3)，

此体积即等于它们的容器中排开水的体积V＝π×52×h，

所以＝π×52×h，

所以h＝，即若取出这两个小球，则水面将下降 cm．

2．已知四面体的各面都是棱长为a的正三角形，求它外接球的体积及内切球的半径．

[解析]　如图，设SO1是四面体S－ABC的高，则外接球的球心O在SO1上．

设外接球半径为R．

∵四面体的棱长为a，O1为正△ABC中心，

∴AO1＝×a＝a，

SO1＝＝＝a，

在Rt△OO1A中，R2＝AO＋OO＝AO＋(SO1－R)2

即R2＝(a)2＋(a－R)2，解得R＝a，

∴所求外接球体积V球＝πR3＝πa3．

∴OO1即为内切球的半径，OO1＝a－a＝a，

∴内切球的半径为a．