数学选修1-21.1回归分析的基本思想及其初步应用学案

这是一份数学选修1-21.1回归分析的基本思想及其初步应用学案，共15页。

哲学知识告诉我们事物之间是有联系的、联系是普遍的，任何事物都是运动的、任何两个事物之间都存在着普遍联系.具体到现实问题中，我们会发现有些问题是从变化的角度来分析是存在两个都在变化的量，关系非常密切，一个现象发生一定量的变化，另一个现象一般也会发生相应的变化，但又不能用函数概念去定义，也无法用函数的模型来代换.如商场销售收入每增加一万元时，因所卖商品不同，销售利润一般会增加不同的数值；施肥量增加一斤，一般地产量也会增加，但数值有时不固定.
5月31日是世界无烟日.有关医学研究表明，许多疾病，例如：心脏病、癌症、脑血管病、慢性阻塞性肺病等都与吸烟有关，吸烟已成为继高血压之后的第二号全球杀手.这些疾病与吸烟有关的结论是怎样得出的呢？若从数学角度区分，这里的疾病和吸烟就是彼此相关的两个变量.
如何用数学的方法来刻画这种变量之间的关系呢？本章要学习的统计案例就是通过对一对变量使用线性回归的方法来研究变量之间的对应关系.通过本章的学习，我们将知道如何研究变量之间的相关关系，如何模拟变量之间的函数关系，如何检验两个变量之间的独立性.
1.1 回归分析的基本思想及其初步应用
Qeq \(\s\up7(情景引入),\s\d5(ing jing yin ru ))
人们常说“名师出高徒”.的确，我们看到很多优秀的老师，他们的学生也非常优秀.但是，名师一定出高徒吗？我们也看到，有些名师的弟子并不高明，甚至比较平庸.
由此可见，名师和高徒之间不是确定性的关系，也不可否认它们之间有着密切的关系，或者说它们之间是密切相关的，但相关性怎样呢？
Xeq \(\s\up7(新知导学),\s\d5(in zhi da xue ))
1.回归分析
(1)概念：回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
(2)步骤：画_散点图__→求_回归方程__→用回归方程进行_预报__.
2.线性回归模型
(1)在线性回归方程eq \(y,\s\up6(^))＝eq \(a,\s\up6(^))＋eq \(b,\s\up6(^))x中，eq \(b,\s\up6(^))＝ eq \f(\i\su(i＝1,n, )xi－\x\t(x)yi－\x\t(y),\i\su(i＝1,n, )xi－\x\t(x)2)＝ eq \f(\i\su(i＝1,n,x)iyi－n\(x,\s\up6(－))\(y,\s\up6(－)),\i\su(i＝1,n,x)\\al(2,i)－n\x\t(x)2) ，eq \(a,\s\up6(^))＝ eq \x\t(y)－eq \(b,\s\up6(^))eq \x\t(x) ，其中eq \x\t(x)＝ eq \f(1,n)eq \i\su(i＝1,n,x)i ，eq \x\t(y) eq \f(1,n)eq \i\su(i＝1,n,y)i ，(eq \x\t(x)，eq \x\t(y))称为变量_样本中心点__，回归直线过样本点的中心.
(2)线性回归模型y＝bx＋a＋e，其中e称为_随机误差__，自变量x称为_解释__变量，因变量y称为_预报__变量.
3.刻画回归效果的方式
Yeq \(\s\up7(预习自测),\s\d5(u xi zi ce ))
1.下列结论正确的是( C )
①函数关系是一种确定性关系；②相关关系是一种非确定性关系；③回归分析是对具有函数关系的两个变量进行统计分析的一种方法；④回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法.
A.①② B.①②③
C.①②④ D.①②③④
[解析] 函数关系和相关关系的区别是前者是确定性关系，后者是非确定性关系，故①②正确；回归分析是对具有相关关系的两个变量进行统计分析的一种方法，故③错误，④正确.故选C.
2.设有一个回归方程为eq \(y,\s\up6(^))＝2－2.5x，当变量x增加一个单位时( C )
A.y平均增加2.5个单位
B.y平均增加2个单位
C.y平均减少2.5个单位
D.y平均减少2个单位
[解析] 由回归方程的系数eq \(b,\s\up6(^))＝－2.5可知，x每增加一个单位，则y平均减少2.5个单位.
3.在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的相关指数R2如下，其中拟合效果最好的模型是( A )
A.模型1的相关指数R2为0.98
B.模型2的相关指数R2为0.80
C.模型3的相关指数R2为0.50
D.模型4的相关指数R2为0.25
[解析] 相关指数R2的取值范围为[0,1]，其中R2＝1，即残差平方和为0，此时预测值与观测值相等，y与x是函数关系，也就是说在相关关系中R2越接近于1，说明随机误差的效应越小，y与x相关程度越大，模型的拟合效果越好.R2＝0，说明模型中x与y无关，故选A.
4.已知变量x和y满足关系y＝－0.1x＋1，变量y与z正相关.下列结论中正确的是( C )
A.x与y正相关，x与z负相关
B.x与y正相关，x与z正相关
C.x与y负相关，x与z负相关
D.x与y负相关，x与z正相关
[解析] 因为y＝－0.1x＋1，－0.1<0，所以x与y负相关.又y与z正相关，故可设z＝ay＋b(a>0)，所以z＝－0.1ax＋a＋b，－0.1a<0.所以x与z负相关.故选C.
5.已知回归直线的斜率的估计值是1.23，样本点的中心为(4,5)，则回归直线方程是 eq \(y,\s\up6(^))＝1.23x＋0.08 .
[解析] 设回归直线方程为eq \(y,\s\up6(^))＝1.23x＋b，
∵回归直线过点(4,5)，
∴5＝1.23×4＋b，
∴b＝0.08，
故回归直线方程为eq \(y,\s\up6(^))＝1.23x＋0.08.
6.已知某种商品的价格x(元)与需求量y(件)之间的关系如以下一组数据：
求y对x的回归直线方程，并说明回归模型拟合效果的好坏.
[解析] eq \x\t(x)＝eq \f(1,5)×(14＋16＋18＋20＋22)＝18.
eq \x\t(y)＝eq \f(1,5)×(12＋10＋7＋5＋3)＝7.4.
eq \i\su(i＝1,5,x)eq \\al(2,i)＝142＋162＋182＋202＋222＝1660.
eq \i\su(i＝1,5,x)iyi＝14×12＋16×10＋18×7＋20×5＋22×3＝620.
所以eq \(b,\s\up6(^))＝eq \f(\i\su(i＝1,5, )xi－\x\t(x)yi－\x\t(y),\i\su(i＝1,5, )xi－\x\t(x)2)
＝eq \f(\i\su(i＝1,5,x)iyi－5\(x,\s\up6(－))\(y,\s\up6(－)),\i\su(i＝1,5,x)\\al(2,i)－5\x\t(x)2)
＝eq \f(620－5×18×7.4,1660－5×182)
＝－1.15.
eq \(a,\s\up6(^))＝7.4＋1.15×18＝28.1.
所求回归直线方程是eq \(y,\s\up6(^))＝－1.15x＋28.1.
列出残差表：
所以eq \i\su(i＝1,5, )(yi－eq \(y,\s\up6(^))i)2＝0.3，eq \i\su(i＝1,5, )(yi－eq \x\t(y))2＝53.2.
R2＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(^))i2,\i\su(i＝1,5, )yi－\x\t(y)2)≈0.994.
所以回归模型的拟合效果好.
Heq \(\s\up7(互动探究解疑 ),\s\d5(u dng tan jiu jie yi ))
命题方向1 ⇨概念的理解和判断
典例1 有下列说法：
①线性回归分析就是由样本点去寻找一条直线，使之贴近这些样本点的数学方法；②利用样本点的散点图可以直观判断两个变量的关系是否可以用线性关系表示；③通过回归方程eq \(y,\s\up6(^))＝eq \(b,\s\up6(^))x＋eq \(a,\s\up6(^))可以估计观测变量的取值和变化趋势；④因为由任何一组观测值都可以求得一个线性回归方程，所以没有必要进行相关性检验.
其中正确命题的个数是( C )
A.1 B.2
C.3 D.4
[思路分析] 由题目可获取以下信息：①线性回归分析；②散点图；③相关性检验等的相关概念及意义.
解答本题可先逐一核对相关概念及其性质，然后再逐一作出判断，最后得出结论.
[解析] ①反映的正是最小二乘法思想，故正确.
②反映的是画散点图的作用，也正确.
③解释的是回归方程eq \(y,\s\up6(^))＝eq \(b,\s\up6(^))x＋eq \(a,\s\up6(^))的作用，故也正确.
④是不正确的，在求回归方程之前必须进行相关性检验，以体现两变量的关系.
『规律方法』 解答概念辨析题，应紧扣线性回归分析中每个概念的定义进行，要准确把握概念的内涵.
〔跟踪练习1〕
下面变量关系是相关关系的是( A )
①学生的学习态度与学习成绩之间的关系；
②教师的执教水平与学生的学习成绩之间的关系；
③学生的身高与学生的学习成绩之间的关系；
④家庭的经济条件与学生的学习成绩之间的关系.
A.①②
B.①③
C.②③
D.②④
[解析] ①②是相关关系，③④是非相关关系.
命题方向2 ⇨线性回归模型
典例2 某种产品的广告费支出x(单位：百万元)与销售额y(单位：百万元)之间有如下对应数据：
(1)画出散点图；
(2)求y关于x的回归方程.
[解析] (1)散点图如图所示.
(2)列出下表，并用科学计算器进行有关计算.
于是可得eq \(b,\s\up6(^))＝eq \f(\i\su(i＝1,5,x)iyi－5\(x,\s\up6(－))\(y,\s\up6(－)),\i\su(i＝1,5,x)\\al(2,1)－5\x\t(x)2)＝eq \f(1 380－5×5×50,145－5×52)＝6.5，
eq \(a,\s\up6(^))＝eq \x\t(y)－eq \(b,\s\up6(^))eq \x\t(x)＝50－6.5×5＝17.5.
于是所求的回归方程是eq \(y,\s\up6(^))＝6.5x＋17.5.
『规律方法』 1.求回归直线方程的一般步骤
(1)作出散点图，依据问题所给的数据在平面直角坐标系中描点，观察点的分布是否呈条状分布，即是否在一条直线附近，从而判断两变量是否具有线性相关关系.
(2)当两变量具有线性相关关系时，求回归系数eq \(a,\s\up6(^))，eq \(b,\s\up6(^))，写出回归直线方程.
2.回归直线方程eq \(y,\s\up6(^))＝eq \(a,\s\up6(^))＋eq \(b,\s\up6(^))x中的eq \(b,\s\up6(^))表示x每增加1个单位时，eq \(y,\s\up6(^))的变化量的估计值为eq \(b,\s\up6(^)).
可以利用回归直线方程eq \(y,\s\up6(^))＝eq \(a,\s\up6(^))＋eq \(b,\s\up6(^))x预报在x取某个值时y的估计值.
由于回归直线中的系数eq \(a,\s\up6(^))和eq \(b,\s\up6(^))是通过样本估计而来的，存在着误差，这种误差可能导致预报结果有偏差.
〔跟踪练习2〕
下表提供了某厂节能降耗技术改造后在生产A产品过程中记录的产量x(t)与相应的生产能耗y(t)的几组对应数据：
根据上表提供的数据，求出y关于x的线性回归方程为eq \(y,\s\up6(^))＝0.7x＋0.35，那么表中t的值为( A )
A.3
C.3.5 D.4.5
[解析] 样本中心点是(eq \(x,\s\up6(－))，eq \(y,\s\up6(－)))，即(4.5，eq \f(11＋t,4)).因为回归直线过该点，所以eq \f(11＋t,4)＝0.7×4.5＋0.35，解得t＝3.
命题方向3 ⇨线性回归分析
典例3 为研究重量x(单位：克)对弹簧长度y(单位：厘米)的影响，对不同重量的6个物体进行测量，数据如下表所示：
(1)作出散点图，并求线性回归方程：
(2)求相关指数R2，并判断模型的拟合效果；
(3)进行残差分析.
[解析] (1)散点图如下图所示：
eq \(x,\s\up6(－))＝eq \f(1,6)×(5＋10＋15＋20＋25＋30)＝17.5，
eq \(y,\s\up6(－))＝eq \f(1,6)×(7.25＋8.12＋8.95＋9.90＋10.9＋11.8)≈9.487，
eq \(∑,\s\up6(6),\s\d4(i＝1))xeq \\al(2,i)＝2 275，eq \(∑,\s\up6(6),\s\d4(i＝1))xiyi＝1 076.2.
计算，得eq \(b,\s\up6(^))≈0.183，eq \(a,\s\up6(^))≈6.285.
所以所求线性回归方程为eq \(y,\s\up6(^))＝6.285＋0.183x.
(2)列表如下：
eq \(∑,\s\up6(6),\s\d4(i＝1)) (yi－eq \(y,\s\up6(^))i)2≈0.013 18，eq \(∑,\s\up6(6),\s\d4(i＝1)) (yi－eq \(y,\s\up6(－)))2≈14.678 1.
所以R2≈1－eq \f(0.013 18,14.678 4)≈0.999 1，
所以回归模型的拟合效果较好.
(3)由表中数据可以看出残差点比较均匀地落在不超过0.15的狭窄的水平带状区域中，说明选用的线性回归模型的精度较高，由以上分析可知，弹簧长度与拉力呈线性关系.由残差表中的数值可以看出第3个样本点的残差比较大，需要确认在采集这个数据的时候是否有人为的错误，如果有的话，需要纠正数据，重新建立回归模型.
『规律方法』 1.线性回归分析的过程：
(1)随机抽取样本，确定数据，形成样本点；
(2)由样本点形成散点图，判定是否具有线性相关关系；
(3)由最小二乘法求线性回归方程；
(4)进行残差分析，分析模型的拟合效果，不合适时，分析错因，予以纠正；
(5)依据回归方程作出预报.
2.用散点图可粗略判断两个变量间有无线性相关关系，用相关指数R2可以描述两个变量之间的密切程度.
〔跟踪练习3〕
一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了10次试验，测得数据如下：
把零件数x作为解释变量，加工时间y作为预报变量.
(1)计算总偏差平方和、残差平方和及相关指数；
(2)作出残差图；
(3)进行残差分析.
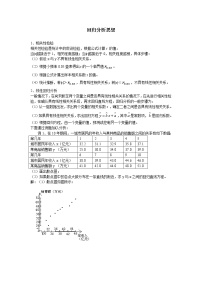
[解析] (1)由x，y的数据得散点图如图.
由散点图可以认为样本点大致分布在某条直线的附近，因此可以用线性回归模型来拟合.设线性回归方程为eq \(y,\s\up6(^))＝eq \(a,\s\up6(^))＋eq \(b,\s\up6(^))x，列出下表：
所以eq \x\t(x)＝55，eq \x\t(y)≈91.7，eq \(b,\s\up6(^))＝eq \f(\(∑,\s\up6(10),\s\d4(i＝1))xiyi－10\x\t(x)\x\t(y),\(∑,\s\up6(10),\s\d4(i＝1))x\\al(2,i)－10\x\t(x)2)＝eq \f(55 950－10×55×91.7,38 500－10×552)≈0.668，eq \(a,\s\up6(^))＝eq \x\t(y)－eq \(b,\s\up6(^)) eq \x\t(x)≈91.7－0.668×55≈54.96.
因此，线性回归方程为eq \(y,\s\up6(^))＝0.668x＋54.96.
将数据代入相应公式可得如下数据表：
所以总偏差平方和为3 688.1，残差平方和为1.408，相关指数R2＝1－eq \f(1.408,3 688.1)≈0.999 6.
(2)作出残差图如图，横坐标为零件数的数据，纵坐标为残差.
(3)由题中数据可得样本相关系数r的值为0.999 8，再结合散点图可以说明x与y有很强的线性相关关系.由R2的值可以看出回归效果很好，也说明用线性回归模型拟合数据效果很好.
由残差图也可以观察到，第4个样本点和第5个样本点的残差比较大，需要确认在采集这两个样本点的过程中是否有人为的错误.
Yeq \(\s\up7(易混易错警示),\s\d5(i hun yi cu jing shi )) 准确理解概念和参数的含义
典例4 关于x与y有如下数据：
为了对x，y两个变量进行统计分析，现有以下两种线性模型：甲模型eq \(y,\s\up6(^))＝6.5x＋17.5，乙模型eq \(y,\s\up6(^))＝7x＋17，试比较哪一个模型拟合的效果更好.
[错解] ∵Req \\al(2,甲)＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(－))i2,\i\su(i＝1,5, )yi－\(y,\s\up6(－))2)＝1－eq \f(155,1 000)＝0.845，
Req \\al(2,乙)＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(－))i2,\i\su(i＝1,5, )yi－\(y,\s\up6(－))2)＝1－eq \f(180,1 000)＝0.82，
∴Req \\al(2,甲)>Req \\al(2,乙).
∴乙模型拟合的效果更好.
[辨析] 明确R2的大小与拟合效果的关系
用相关指数R2来比较模型的拟合效果，R2越大，模型的拟合效果越好，并不是R2越小模型的拟合效果越好.
[正解] ∵Req \\al(2,甲)＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(－))i2,\i\su(i＝1,5, )yi－\(y,\s\up6(－))2)＝1－eq \f(155,1 000)＝0.845，
Req \\al(2,乙)＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(－))i2,\i\su(i＝1,5, )yi－\(y,\s\up6(－))2)＝1－eq \f(180,1 000)＝0.82，
∴Req \\al(2,甲)>Req \\al(2,乙).
∴甲模型拟合的效果更好.
〔跟踪练习4〕
甲、乙、丙、丁4位同学各自对A，B两个变量进行回归分析，分别得到散点图与残差平方和eq \i\su(i＝1,n, )(yi－eq \(y,\s\up6(^))i)2如表：
哪位同学的试验结果体现A，B两变量关系的模型拟合精度高？( D )
A.甲 B.乙
C.丙 D.丁
Xeq \(\s\up7(学科核心素养),\s\d5(ue ke he xin su yang)) 可线性化的回归分析
当回归方程不是形如y＝bx＋a(a(1)作散点图确定曲线模型
因为曲线所对应的函数种类繁多，这就要求我们充分想象，大胆猜测拟合函数类型，估计使用哪个函数拟合.
(2)非线性转化为线性
先通过适当变换化非线性关系为线性关系：
①指数型：y＝cax(a>0且a≠1，c>0，a，c为常数).
两边取自然对数ln y＝ln(cax)，
即ln y＝ln c＋xln a，
令eq \b\lc\{\rc\ (\a\vs4\al\c1(y′＝ln y,x′＝x，))原方程变为y′＝ln c＋x′ ln a，
然后按线性回归模型求出ln a，ln c.
②对数型：y＝a＋bln x(a，b为常数，x>0).
令eq \b\lc\{\rc\ (\a\vs4\al\c1(y′＝y，,x′＝ln x，))原方程变为y′＝a＋bx′，
然后按线性回归模型求出a，b.
③幂函数：y＝axn(a，n为常数，a，x均取正值).
两边取常用对数lg y＝lg(axn)，
即lg y＝nlg x＋lg a，
令eq \b\lc\{\rc\ (\a\vs4\al\c1(y′＝lg y，,x′＝lg x，))原方程变为y′＝nx′＋lg a，
然后按线性回归模型求出n，lg a.
④y＝bx2＋a型(a，b为常数).
令eq \b\lc\{\rc\ (\a\vs4\al\c1(y′＝y，,x′＝x2，))原方程变为y′＝bx′＋a，
然后按线性回归模型求出a，b.
⑤y＝a＋eq \f(b,x)型(a，b为常数，x≠0).
令eq \b\lc\{\rc\ (\a\vs4\al\c1(y′＝y,x′＝\f(1,x)，))原方程变为y′＝a＋bx′，
然后按线性回归模型求出a，b.
(3)分析模型的拟合效果
对于同一问题可以有几种不同的拟合模型，对于给定的样本点(x1，y1)，(x1，y2)，…，(xn，yn)，可以通过以下几种方式确定选用哪种模型更合适.
①可以根据转换后的对应数据作散点图来确定线性回归的拟合情况，判断使用哪一种曲线模型较为合适.
②可以通过原始数据及y和x之间的非线性回归方程列出残差对比分析表，一般通过残差平方和比较两种模型的拟合效果，其中残差平方和较小的拟合效果较好.
③还可以用R2来比较模型的拟合效果，R2越大(越接近1)，拟合效果越好.
典例5 在一化学反应过程中，某化学物质的反应速率y(g/min)与一种催化剂的量x(g)有关，现收集了如下表所示的8组数据，试建立y与x之间的回归方程.
[解析] 根据收集的数据作散点图如图.
根据样本点的分布情况，可选用指数型函数模型y＝c1e (c1，c2为待定的参数)，
令z＝ln y，则z＝c2x＋ln c1，
即变换后样本点应该分布在直线z＝bx＋a(a＝ln c1，b＝c2)的附近，由y与x的数据表得z与x的数据表如下：
作出z与x的散点图如图
由图可以看出变换后的样本点分布在一条直线附近，所以可用回归直线方程来拟合.
由表中数据可得
eq \(b,\s\up6(^))≈0.1812，eq \(a,\s\up6(^))≈－0.8485，
故eq \(z,\s\up6(^))＝0.1812x－0.8485，
所以eq \(y,\s\up6(^))＝e0.1812x－0.8485，
因此，该化学物质的反应速率与催化剂的量之间的非线性回归方程为eq \(y,\s\up6(^))＝e0.1812x－0.8485.
『规律方法』 解决非线性回归问题的具体做法是：(1)若问题中已给出经验公式，可以将解释变量进行变换(换元)，将变量的非线性关系转化为线性关系，将问题转化为线性回归分析问题解决.(2)若问题中没有给出经验公式，需要画出已知数据的散点图，通过与各种函数(指数函数、对数函数、幂函数等)的图象作比较，选择与这些散点拟合最好的函数，然后采用适当的变量变换，将问题转化为线性回归问题解决.
Keq \(\s\up7(课堂达标验收),\s\d5(e tang da bia yan shu))
1.在画两个变量的散点图时，下列叙述正确的是( B )
A.预报变量在x轴上，解释变量在y轴上
B.解释变量在x轴上，预报变量在y轴上
C.可以选择两个变量中任意一个变量在x轴上
D.可以选择两个变量中任意一个变量在y轴上
2.下列哪些变量是相关关系( C )
A.出租车车费与行驶的路程
B.房屋面积与房屋价格
C.人的身高与体重
D.铁块的大小与质量
3.已知某人加工零件的个数x与花费时间y(h)之间的线性回归方程为eq \(y,\s\up6(^))＝0.01x＋0.5，则加工600个零件大约需要_6.5__h.
4.已知某商品的价格x(元)与需求量y(件)之间的关系有如下一组数据：
(1)画出y关于x的散点图；
(2)求出回归直线方程；
(3)计算R2的值，并说明回归模型拟合程度的好坏.
(参考数据：eq \x\t(x)＝18，eq \x\t(y)＝7.4，eq \(∑,\s\up6(5),\s\d4(i＝1))xeq \\al(2,i)＝1660，eq \i\su(i＝1,5,y)eq \\al(2,i)＝327，eq \i\su(i＝1,5,x)iyi＝620，eq \i\su(i＝1,5, )(yi－eq \(y,\s\up6(^))i)2＝0.3，eq \i\su(i＝1,5, )(yi－eq \x\t(y))2＝53.2.)
[解析] （1）散点图如图所示：
(2)因为eq \x\t(x)＝18，eq \x\t(y)＝7.4，eq \(∑,\s\up6(5),\s\d4(i＝1))xeq \\al(2,i)＝1660，eq \i\su(i＝1,5,y)eq \\al(2,i)＝327，eq \i\su(i＝1,5,x)iyi＝620，
所以eq \(b,\s\up6(^))＝eq \f(\i\su(i＝1,5,x)iyi－5\x\t(x) \x\t(y),\i\su(i＝1,5,x)\\al(2,i)－5\x\t(x)2)＝－1.15，
eq \(a,\s\up6(^))＝eq \x\t(y)－eq \(b,\s\up6(^))eq \x\t(x)＝28.1.
即所求回归直线方程为eq \(y,\s\up6(^))＝－1.15x＋28.1.
(3)因为eq \i\su(i＝1,5, )(yi－eq \(y,\s\up6(^))i)2＝0.3，eq \i\su(i＝1,5, )(yi－eq \x\t(y))2＝53.2，
所以R2＝1－eq \f(\i\su(i＝1,5, )yi－\(y,\s\up6(^))i2,\i\su(i＝1,5, )yi－\x\t(y)2)≈0.994，
故回归模型的拟合效果较好.
残差
把随机误差的估计值eq \(e,\s\up6(^))i称为相应于点(xi，yi)的残差
残差图
作图时纵坐标为_残差__，横坐标可以选为_样本编号__，或_身高数据__，或_体重估计值__等，这样作出的图形称为残差图
残差图法
残差点比较均匀地落在水平的带状区域中，说明选用的模型比较合适，这样的带状区域的宽度_越窄__，说明模型拟合精度越高
残差平方和
残差平方和为 eq \(∑,\s\up6(n),\s\d4(i＝1)) (yi－eq \(y,\s\up6(^))i)2 ，残差平方和_越小__，模型拟合效果越好
相关指数R2
R2＝1－ eq \f(\i\su(i＝1,n, )yi－\(y,\s\up6(^))i2,\i\su(i＝1,n, )yi－\x\t(y)2) ，R2表示_解释__变量对_预报__变量变化的贡献率，R2越接近于1，表示回归的效果越好
x
14
16
18
20
22
y
12
10
7
5
3
yi－eq \(y,\s\up6(^))i
0
0.3
－0.4
－0.1
0.2
yi－eq \x\t(y)
4.6
2.6
－0.4
－2.4
－4.4
x
2
4
5
6
8
y
30
40
60
50
70
i
1
2
3
4
5
xi(百万元)
2
4
5
6
8
yi(百万元)
30
40
60
50
70
xiyi
60
160
300
300
560
eq \x\t(x)＝5；eq \x\t(y)＝50；
eq \i\su(i＝1,5,x)eq \\al(2,i)＝145；eq \i\su(i＝1,5,x)iyi＝1 380
x
3
4
5
6
y
2.5
t
4
4.5
x
5
10
15
20
25
30
y
7.25
8.12
8.95
9.90
10.9
11.8
yi－eq \(y,\s\up6(^))i
0.05
0.005
－0.08
－0.045
0.04
0.025
yi－eq \(y,\s\up6(－))
－2.24
－1.37
－0.54
0.41
1.41
2.31
零件数x(个)
10
20
30
40
50
60
70
80
90
100
加工时间y(min)
62
68
75
81
89
95
102
108
115
122
i
1
2
3
4
5
xi(个)
10
20
30
40
50
yi(min)
62
68
75
81
89
xiyi
620
1 360
2 250
3 240
4 450
i
6
7
8
9
10
xi(个)
60
70
80
90
100
yi(min)
95
102
108
115
122
xiyi
5 700
7 140
8 640
10 350
12 200
零件数x(个)
10
20
30
40
50
加工时间y(min)
62
68
75
81
89
(yi－eq \x\t(y))2
882.09
561.69
278.89
114.49
7.29
eq \(y,\s\up6(^))＝0.668x＋54.96
61.64
68.32
75.0
81.68
88.36
残差
0.36
－0.32
0
－0.68
0.64
零件数x(个)
60
70
80
90
100
加工时间y(min)
95
102
108
115
122
(yi－eq \x\t(y))2
10.89
106.09
265.69
542.89
918.09
eq \(y,\s\up6(^))＝0.668x＋54.96
95.04
101.72
108.4
115.08
121.76
残差
－0.04
0.28
－0.4
－0.08
0.24
x
2
4
5
6
8
y
30
40
60
50
70
甲
乙
丙
丁
散点图
残差平方和
115
106
124
103
催化剂的量x(g)
15
18
21
24
27
30
33
36
化学物质反应速率y(g/min)
6
8
30
27
70
205
65
350
x
15
18
21
24
27
30
33
36
z
1.792
2.079
3.401
3.296
4.248
5.323
4.174
5.858
x
14
16
18
20
22
y
12
10
7
5
3