新高考数学一轮复习教师用书：第四章　7 第7讲　正弦定理与余弦定理学案

这是一份新高考数学一轮复习教师用书：第四章　7 第7讲　正弦定理与余弦定理学案，共21页。
第7讲　正弦定理与余弦定理


1．正弦定理和余弦定理
定理
正弦定理
余弦定理
内容
＝＝＝2R(R为△ABC外接圆半径)
a2＝b2＋c2－2bccos__A；
b2＝c2＋a2－2cacos__B；
c2＝a2＋b2－2abcos__C
变形形式
a＝2Rsin__A，b＝2Rsin__B，
c＝2Rsin__C；
sin A＝，sin B＝，
sin C＝；
a∶b∶c＝sin__A∶sin__B∶sin__C；
＝
cos A＝；
cos B＝；
cos C＝
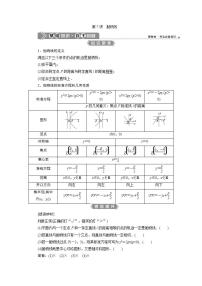
2.三角形解的判断

A为锐角
A为钝角
或直角
图形




关系式
a＝bsin A
bsin Asin B的充分不必要条件是A>B.(　　)
(4)在△ABC中，a2＋b21.
所以角B不存在，即满足条件的三角形不存在．
2．在△ABC中，若sin A＝sin B，则A，B的关系为________；若sin A>sin B，则A，B的关系为________．
解析：sin A＝sin B⇔a＝b⇔A＝B；
sin A>sin B⇔a>b⇔A>B.
答案：A＝B　A>B
3．在△ABC中，acos A＝bcos B，则这个三角形的形状为________．
解析：由正弦定理，得sin Acos A＝sin BcosB，
即sin 2A＝sin 2B，所以2A＝2B或2A＝π－2B，
即A＝B或A＋B＝，
所以这个三角形为等腰三角形或直角三角形．
答案：等腰三角形或直角三角形


　　　　　　利用正弦、余弦定理解三角形(高频考点)
利用正、余弦定理解三角形是高考的热点，三种题型在高考中时有出现，其试题为中档题．主要命题角度有：
(1)由已知求边和角；
(2)三角恒等变换与解三角形．
角度一　由已知求边和角
(1)(2020·金华市东阳二中高三调研)在△ABC中，角A，B，C所对的边分别为a，b，c，若3bcos A＝ccos A＋acos C，则tan A的值是(　　)
A．－2　　　　　　　　 B．－
C．2 D.
(2)(2019·高考浙江卷)在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D在线段AC上．若∠BDC＝45°，则BD＝________，cos∠ABD＝________．
【解析】　(1)因为△ABC中，由余弦定理得
ccos A＋acos C＝c×＋a×＝b.
所以根据题意，3bcos A＝ccos A＋acos C＝b，
两边约去b，得3cos A＝1，所以cos A＝>0，
所以A为锐角，且sin A＝＝，
因此，tan A＝＝2.
(2)在Rt△ABC中，易得AC＝5，sin C＝＝.在△BCD中，由正弦定理得BD＝×sin∠BCD＝×＝，sin∠DBC＝sin[π－(∠BCD＋∠BDC)]＝sin(∠BCD＋∠BDC)＝sin ∠BCDcos∠BDC＋cos∠BCDsin∠BDC＝×＋×＝.又∠ABD＋∠DBC＝，所以cos∠ABD＝sin∠DBC＝.
【答案】　(1)C　(2)　
角度二　三角恒等变换与解三角形
在△ABC中，内角A，B，C所对的边分别为a，b，c.已知b＋c＝2acos B.
(1)证明：A＝2B；
(2)若cos B＝，求cos C的值．
【解】　(1)证明：由正弦定理得sin B＋sin C
＝2sin Acos B，
故2sin Acos B＝sin B＋sin(A＋B)＝sin B＋sin Acos B＋cos Asin B，于是sin B＝sin(A－B)．
又A，B∈(0，π)，
故0＜A－B＜π，
所以B＝π－(A－B)或B＝A－B，
因此A＝π(舍去)或A＝2B，
所以A＝2B.
(2)由cos B＝得sin B＝，
cos 2B＝2cos2B－1＝－，
故cos A＝－，sin A＝，
cos C＝－cos(A＋B)＝－cos Acos B＋sin Asin B＝.

(变问法)本例条件不变，若△ABC的面积S＝，求角A的大小．
解：由S＝，得absin C＝，故有
sin Bsin C＝sin 2B＝sin Bcos B，
因为sin B≠0，所以sin C＝cos B，
又B，C∈(0，π)，所以C＝±B.
当B＋C＝时，A＝；
当C－B＝时，A＝.
综上，A＝或A＝.

(1)正、余弦定理的选用
解三角形时，如果式子中含有角的正弦或边的一次式时，则考虑用正弦定理；如果式子中含有角的余弦或边的二次式时，要考虑用余弦定理；以上特征都不明显时，则要考虑两个定理都有可能用到．
(2)三角形解的个数的判断
已知两角和一边，该三角形是确定的，其解是唯一的；已知两边和一边的对角，该三角形具有不唯一性，通常根据三角函数值的有界性和大边对大角定理进行判断．　

1．△ABC的内角A、B、C的对边分别为a、b、c.已知sin B＋sin A(sin C－cos C)＝0，a＝2，c＝，则C＝(　　)
A. B.
C. D.
解析：选B.因为sin B＋sin A(sin C－cos C)＝0，所以sin(A＋C)＋sin Asin C－sin Acos C＝0，所以sin Acos C＋cos Asin C＋sin Asin C－sin Acos C＝0，整理得sin C·(sin A＋cos A)＝0，因为sin C≠0，所以sin A＋cos A＝0，所以tan A＝－1，因为A∈(0，π)，所以A＝，由正弦定理得sin C＝＝＝，又0