新高考数学一轮复习教师用书：第九章　1 第1讲　直线的倾斜角与斜率、直线的方程学案

这是一份新高考数学一轮复习教师用书：第九章　1 第1讲　直线的倾斜角与斜率、直线的方程学案，共17页。

知识点
最新考纲
直线的方程
理解平面直角坐标系，理解直线的倾斜角与斜率的概念，掌握直线方程的点斜式、两点式及一般式，了解直线方程与一次函数的关系.
两直线的位置关系
能根据两条直线的斜率判定这两条直线平行或垂直．
会求过两点的直线斜率、两直线的交点坐标、两点间的距离、点到直线的距离、两条平行直线间的距离．
圆的方程
掌握圆的标准方程与一般方程．
直线、圆的位置关系
会解决直线与圆的位置关系的问题，会判断圆与圆的位置关系．
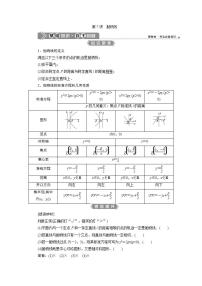
椭 圆
掌握椭圆的定义、标准方程、几何图形及简单几何性质．
会解决直线与椭圆的位置关系的问题．
双曲线
了解双曲线的定义、标准方程、几何图形及简单几何性质，了解直线与双曲线的位置关系．
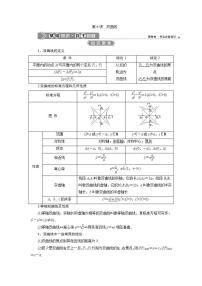
抛物线
掌握抛物线的定义、标准方程、几何图形及简单几何性质．
会解决直线与抛物线的位置关系的问题．
曲线与方程
了解方程与曲线的对应关系．会求简单的曲线的方程.
第1讲　直线的倾斜角与斜率、直线的方程


1．直线的倾斜角
(1)定义：x轴正向与直线向上方向之间所成的角叫做这条直线的倾斜角．当直线与x轴平行或重合时，规定它的倾斜角为0°．
(2)倾斜角的范围为[0，π)．
2．直线的斜率
(1)定义：一条直线的倾斜角α的正切值叫做这条直线的斜率，斜率常用小写字母k表示，即k＝tan α，倾斜角是90°的直线没有斜率．
(2)过两点的直线的斜率公式
经过两点P1(x1，y1)，P2(x2，y2)(x1≠x2)的直线的斜率公式为k＝＝.
3．直线方程的五种形式
名称
已知条件
方程
适用范围
点斜式
斜率k与点(x1，y1)
y－y1＝k(x－x1)
不含直线x＝x1
斜截式
斜率k与直线在y轴上的截距b
y＝kx＋b
不含垂直于x轴的直线
两点式
两点(x1，y1)，(x2，y2)
＝
(x1≠x2，y1≠y2)
不含直线x＝x1(x1＝x2)和直线y＝y1(y1＝y2)
截距式
直线在x轴、y轴上的截距分别为a，b
＋＝1
(a≠0，b≠0)
不含垂直于坐标轴和过原点的直线
一般式

Ax＋By＋C＝0
(A2＋B2≠0)
平面直角坐标系内的直线都适用

[疑误辨析]
判断正误(正确的打“√”，错误的打“×”)
(1)直线的倾斜角越大，其斜率就越大．(　　)
(2)直线的斜率为tan α，则其倾斜角为α.(　　)
(3)斜率相等的两直线的倾斜角不一定相等．(　　)
(4)经过点P(x0，y0)的直线都可以用方程y－y0＝k(x－x0)表示．(　　)
(5)经过任意两个不同的点P1(x1，y1)，P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示．(　　)
答案：(1)×　(2)×　(3)×　(4)×　(5)√
[教材衍化]
1．(必修2P86练习T3改编)若过点M(－2，m)，N(m，4)的直线的斜率等于1，则m的值为________．
解析：由题意得＝1，解得m＝1.
答案：1
2．(必修2P100A组T8改编)直线3x－4y＋k＝0在两坐标轴上的截距之和为2，则实数k＝________．
解析：令x＝0，得y＝； 令y＝0，得x＝－，则有－＝2，所以k＝－24.
答案：－24
[易错纠偏]
(1)由直线方程求斜率的思路不清；
(2)忽视斜率和截距对直线位置的影响；
(3)忽视直线斜率不存在的情况；
(4)忽视截距为0的情况．
1．直线l：xsin 30°＋ycos 150°＋a＝0的斜率为________．
解析：设直线l的斜率为k，则k＝－＝.
答案：
2．如果A·C0，故直线经过第一、二、四象限，不经过第三象限．
答案：三
3．过直线l：y＝x上的点P(2，2)作直线m，若直线l，m与x轴围成的三角形的面积为2，则直线m的方程为________．
解析：①若直线m的斜率不存在，则直线m的方程为x＝2，直线m，直线l和x轴围成的三角形的面积为2，符合题意；②若直线m的斜率k＝0，则直线m与x轴没有交点，不符合题意；③若直线m的斜率k≠0，设其方程为y－2＝k(x－2)，令y＝0，得x＝2－，依题意有××2＝2，即＝1，解得k＝，所以直线m的方程为y－2＝(x－2)，即x－2y＋2＝0.综上可知，直线m的方程为x－2y＋2＝0或x＝2.
答案：x－2y＋2＝0或x＝2
4．过点P(2，3)且在两坐标轴上截距相等的直线方程为________．
解析：当截距为0时，直线方程为3x－2y＝0；
当截距不为0时，设直线方程为＋＝1，
则＋＝1，解得a＝5，所以直线方程为x＋y－5＝0.
答案：3x－2y＝0或x＋y－5＝0


　　　　　　直线的倾斜角与斜率
(1)直线2xcos α－y－3＝0的倾斜角的变化范围是(　　)
A.　　　　　　　　 B.
C. D.
(2)已知直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则实数m的取值范围是(　　)
A．[－，]
B.∪
C.∪
D．以上都不对
【解析】　(1)直线2xcos α－y－3＝0的斜率k＝2cos α.由于α∈，所以≤cos α≤，因此k＝2cos α∈[1，]．设直线的倾斜角为θ，则有tan θ∈[1，]．由于θ∈[0，π)，所以θ∈，即倾斜角的变化范围是.
(2)设M(x，y)，由kMA·kMB＝3，得·＝3，即y2＝3x2－3.
联立得x2＋x＋6＝0.
要使直线l：x－my＋m＝0上存在点M满足与两点A(－1，0)，B(1，0)连线的斜率kMA与kMB之积为3，则Δ＝－24≥0，即m2≥.所以实数m的取值范围是∪.故选C.
【答案】　(1)B　(2)C

(变条件)若本例(1)中直线变为x＋ycos θ－3＝0(θ∈R)，则直线的倾斜角α的取值范围为________．
解析：当cos θ＝0时，方程变为x－3＝0，其倾斜角为；
当cos θ≠0时，由直线的方程，可得斜率k＝－.
因为cos θ∈[－1，1]且cos θ≠0，
所以k∈(－∞，－1]∪[1，＋∞)，
即tan α∈(－∞，－1]∪[1，＋∞)，
又α∈[0，π)，所以α∈∪，
综上知，直线的倾斜角α的取值范围是.
答案：

(1)求倾斜角的取值范围的一般步骤
①求出斜率k＝tan α的取值范围．
②利用三角函数的单调性，借助图象，确定倾斜角α的取值范围．
[提醒]　求倾斜角时要注意斜率是否存在．
(2)斜率的求法
①定义法：若已知直线的倾斜角α或α的某种三角函数值，一般根据k＝tan α求斜率．
②公式法：若已知直线上两点A(x1，y1)，B(x2，y2)，一般根据斜率公式k＝(x1≠x2)求斜率．　

1．若直线l的斜率为k，倾斜角为α，且α∈∪，则k的取值范围是________．
解析：当α∈时，k＝tan α∈；
当α∈时，k＝tan α∈[－，0)．
综上k∈[－，0)∪.
答案：[－，0)∪
2．若经过点P(1－a，1＋a)和Q(3，2a)的直线的倾斜角为锐角，则实数a的取值范围是________．
解析：由条件知直线的斜率存在，
由斜率公式得k＝.
因为倾斜角为锐角，所以k>0，解得a>1或ab>c>0，
所以