2020-2021学年4 平行线的性质课文内容课件ppt

这是一份2020-2021学年4 平行线的性质课文内容课件ppt，共19页。PPT课件主要包含了量一量，拼一拼，∠1∠2，平行线的性质1，∴∠1∠2，∵a∥b，简写为，符号语言，平行线的性质2，∴∠2∠3等内容，欢迎下载使用。

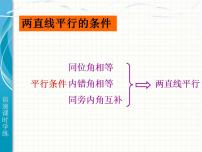
平行线的判定方法是什么？1、同位角相等，两直线平行.2、内错角相等，两直线平行.3、同旁内角互补，两直线平行. 反过来，如果两条直线平行，同位角、内错角、同旁内角各有什么关系呢？
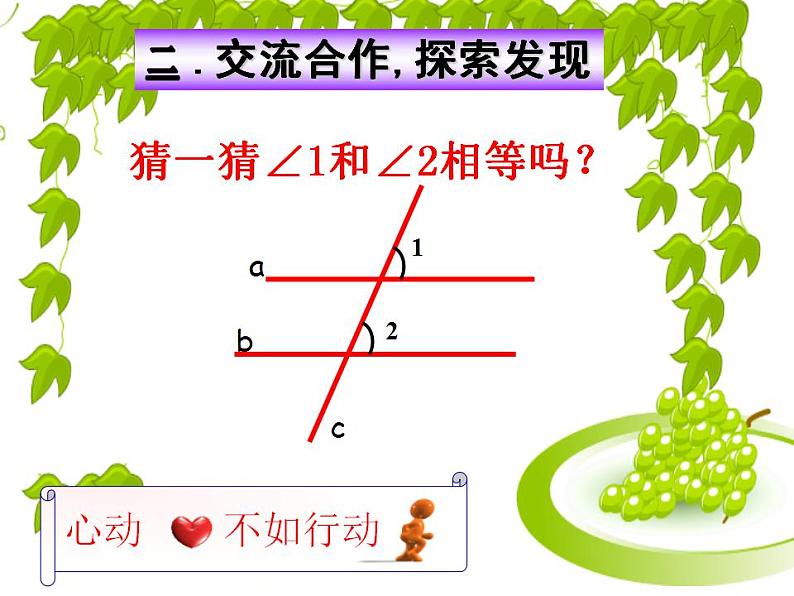
.交流合作,探索发现
猜一猜∠1和∠2相等吗？
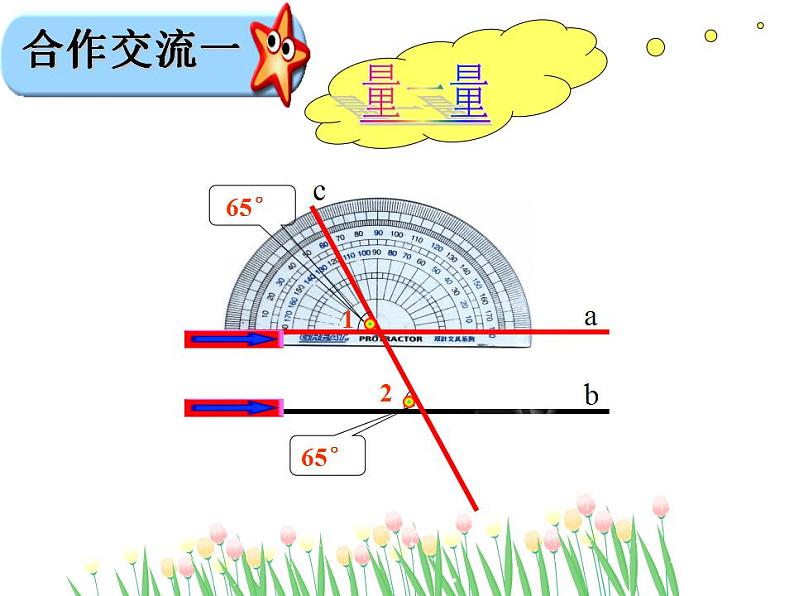
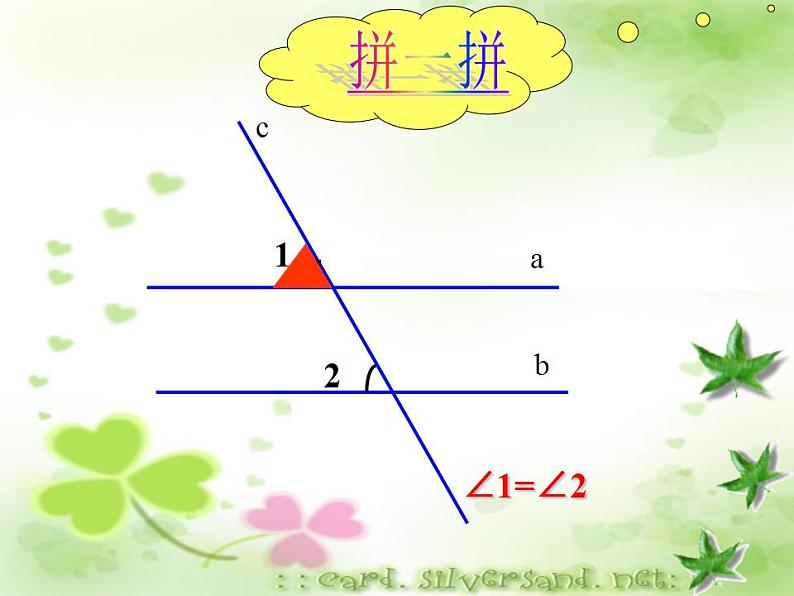
两直线平行，同位角相等.
两条平行线被第三条直线所截， 同位角相等.
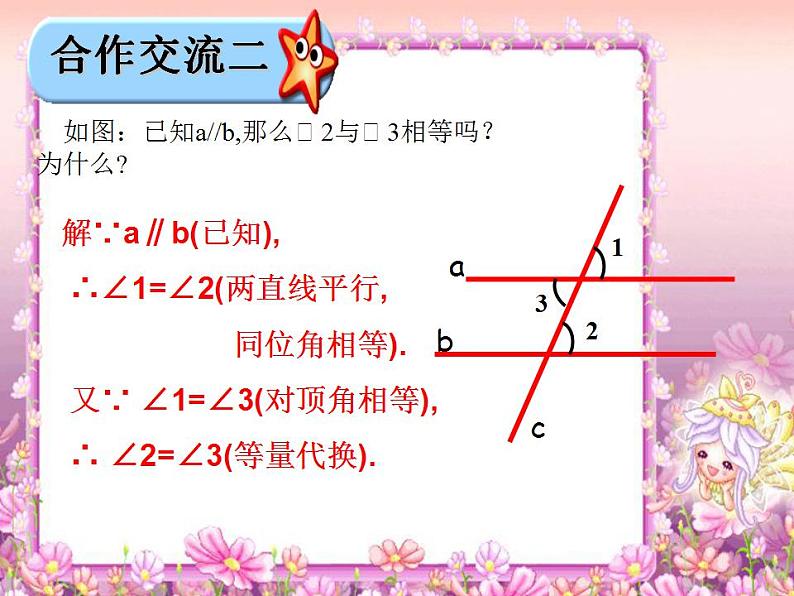
如图：已知a//b,那么2与3相等吗？为什么?
解∵a∥b(已知), ∴∠1=∠2(两直线平行, 同位角相等). 又∵ ∠1=∠3(对顶角相等), ∴ ∠2=∠3(等量代换).
两直线平行，内错角相等.
两条平行线被第三条直线所截， 内错角相等.
解： ∵a//b （已知）,
如图,已知a//b,那么2与4有什么关系呢？为什么?
∴ 1=  2（两直线平行， 同位角相等）.
∵  1+  4=180° （邻补角定义）,
∴ 2+  4=180° （等量代换）.
两直线平行，同旁内角互补.
两条平行线被第三条直线所截， 同旁内角互补.
∴ 2+  4=180°.
例 如图,已知直线a∥b,∠1 = 500,求∠2的度数.
∴∠ 2= 500 (等量代换).
解：∵ a∥b(已知),
∴∠ 1= ∠ 2(两直线平行,内错角相等).
又∵∠ 1 = 500 (已知),
变式１：已知条件不变，求∠3，∠4的度数？
变式2:已知∠3 =∠4，∠1=47°,求∠2的度数？
∴∠ 2= 470（ ）
解：∵ ∠3 =∠4( )
∴a∥b( )
又∵∠ 1 = 470 ( )
两直线平行，同位角相等
同位角相等,两直线平行
巩固知识，拓展提高
如图在四边形ABCD中,已知AB∥CD,∠B = 600.①求∠C的度数;②由已知条件能否求得∠A的度数?
解: ① ∵ AB∥CD(已知),∴ ∠B + ∠C= 1800(两直线平行,同旁内角互补).又∵ ∠B = 600 (已知),∴∠C = 1200 (等式的性质).
②根据题目的已知条件,无法求出∠A的度数.
（1）∵∠ADE=60 ° ∠B=60 °
(同位角相等，两直线平行)
(两直线平行，同位角相等)
已知　∠ADE=60 ° ∠B=60 °∠AED=40°证：（１）DE∥BC（２） ∠C的度数
梳理知识，颗粒归仓
平行线的性质和平行线的判定方法的 区 别 与 联 系
2、证明的一般步骤（1）根据题意，画出图形．（2）根据条件、结论，结合图形，写出已知、求证.（3）经过分析，写出证明过程．