数学7.1.4 平面向量的数乘运算授课课件ppt

这是一份数学7.1.4 平面向量的数乘运算授课课件ppt，共32页。PPT课件主要包含了创设情境兴趣导入，动脑思考探索新知，巩固知识典型例题，运用知识强化练习，a+b，记作a＋b即，利用计算器求得，一般地有，自我反思目标检测等内容，欢迎下载使用。

如图所示，用100N的力，按照不同的方向拉一辆车，效果一样吗？
在数学与物理学中，有两种量．只有大小，没有方向的量
量做数量（标量） ，例如质量、时间、温度、面积、密度等．
既有大小，又有方向的量叫做向量（矢量），
平面上带有指向的线段（有向线段）叫
做平面向量，指向就是向量的方向，线段
的长度表示向量的大小．如右图所示，有向
线段的起点叫做平面向量的起点，有向线段的终
点叫做平面向量的终点．以A为起点，B为终点
也可以使用小写英文字母，印
刷用黑体表示，记作a；手写时应在字母上面
向量的大小叫做向量的模．向量a,
模为零的向量叫做零向量．记作0，
零向量的方向是不确定的．
模为1的向量叫做单位向量．
做数量（标量） ，例如质量、时间、温度、面积、密度等．
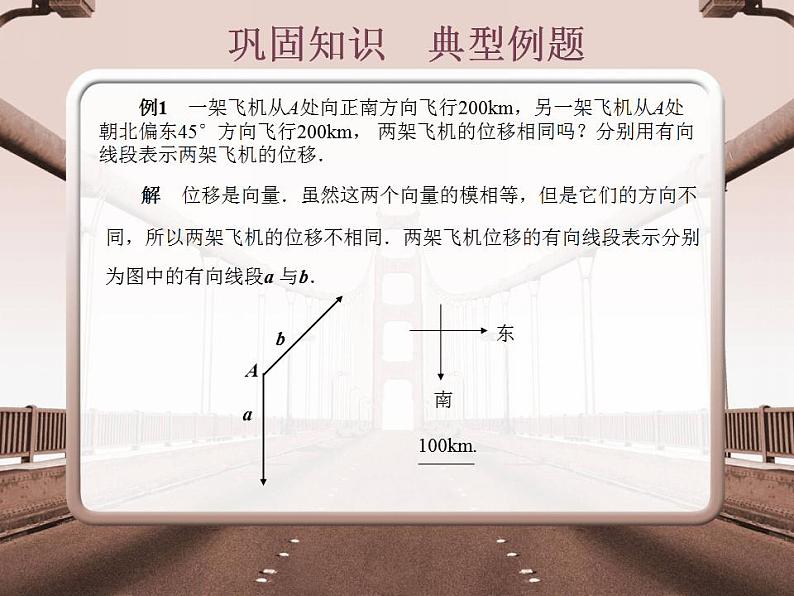
　　例1　一架飞机从A处向正南方向飞行200km，另一架飞机从A处朝北偏东45°方向飞行200km， 两架飞机的位移相同吗？分别用有向线段表示两架飞机的位移．
解　位移是向量．虽然这两个向量的模相等，但是它们的方向不
同，所以两架飞机的位移不相同．两架飞机位移的有向线段表示分别
为图中的有向线段a 与b．
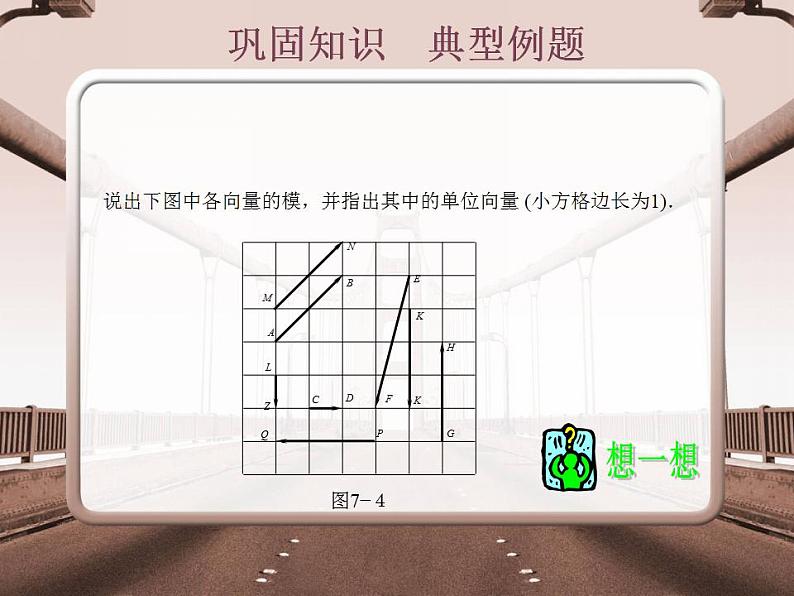
说出下图中各向量的模，并指出其中的单位向量 (小方格边长为1)．
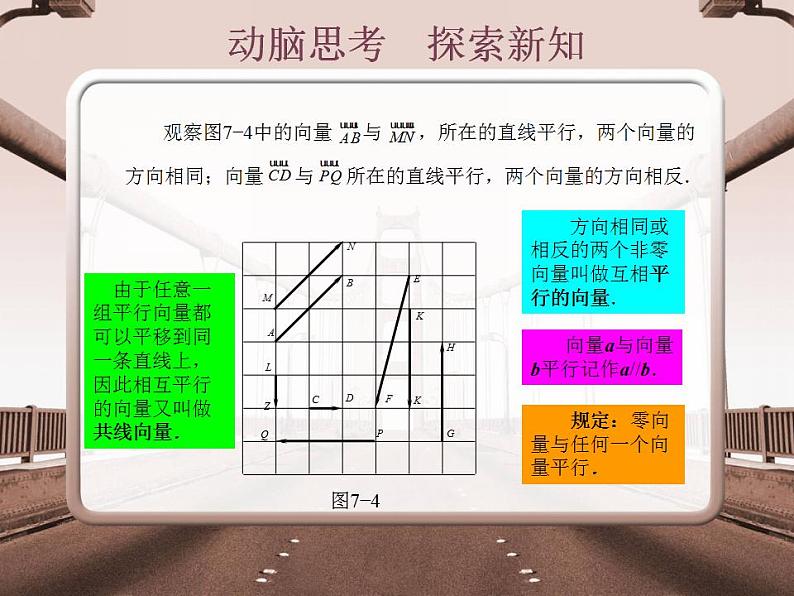
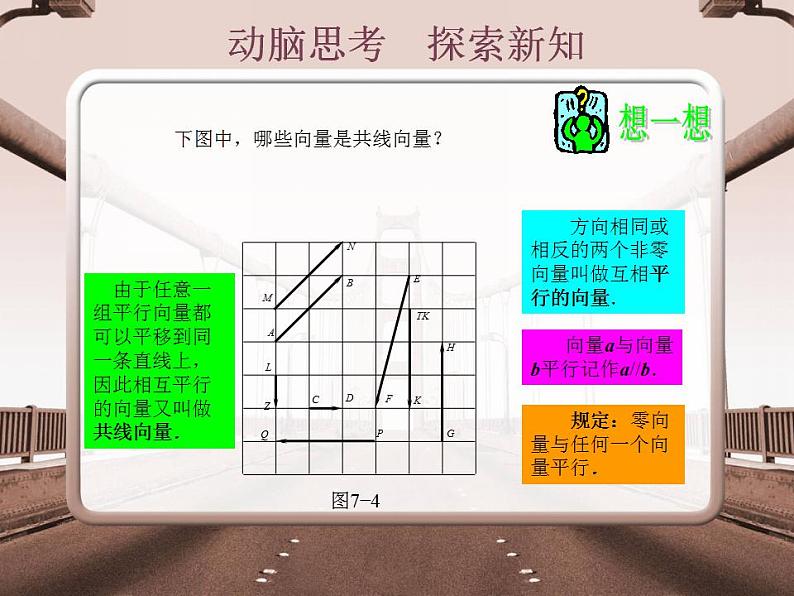
　　方向相同或相反的两个非零向量叫做互相平行的向量．
向量a与向量b平行记作a//b．
　　规定：零向量与任何一个向量平行．
　由于任意一组平行向量都可以平移到同一条直线上，因此相互平行的向量又叫做共线向量．
下图中，哪些向量是共线向量？
　　向量只有大小与方向两个要素．当向量a与向量b的模相等并且方向相同时，称向量a与向量b相等，记作a = b ．
　　与非零向量的模相等，且方向相反的向量叫做向量的负向量，记作 －a．
　　规定：零向量的负向量仍为零向量．
　　例2　在平行四边形ABCD中（图7－5），O为对角线交点．
　　例2　在平行四边形ABCD中（图7－4），O为对角线交点．
解 由平行四边形的性质，得
2．如图，O点是正六边形ABCDEF的中心，试写出
王涛同学从家中（A处）出发，向正南方向行走500 m到
达超市（B处），买了文具后，又沿着北偏东60°角方向行
走200 m到达学校（C处）（如
总效果是从家（A处）到达了学
图）．王涛同学这两次位移的
一般地，设向量a与向量b不共线，在平面上任取一点A
求向量的和的运算叫做向量的加法．上述求向量的和的方法
叫做向量加法的三角形法则．
（1）a＋b与b＋a相等吗？请画出图来说明．
（2）如果向量a和向量b共线，如何画出它们的和向量？
如图所示，ABCD为平行四边形，由于
平行四边形法则不适用于共线向量，可以验证，向量的加法具有以下的性质：
(1) a＋0 = 0＋a=a； a＋（− a）= 0；
(2) a＋b = b＋a；
(3) （a＋b）＋ c = a ＋（b＋c）．
例3 一艘船以12 km/h的速度航行，方向垂直于河岸，已知水流速度为5 km/h，求该船的实际航行速度．
速度，由向量加法的平行四边形法则，
例4 用两条同样的绳子挂一个物体,设物体的重力为k，两条
，求物体受到沿两条绳子的方向的
解 利用平行四边形法则，可以得到
根据例题4的分析，判断在单杠上悬挂身体时，两臂
成什么角度时，双臂受力最小？
与数的运算相类似，可以将向量a与向量b的负向量的和定义
为向量a与向量b的差．即
a − b = a＋(−b)．
观察图可以得到：起点相同的
个向量，其起点是减向量b的终点，
两个向量a、 b，其差a − b仍然是一
终点是被减向量a的终点．
例5 已知如图所示向量a 、b ，请画出向量a − b．
解 如图所示，以平面上任一点O
3a是一个向量，其方向与a的方向相同,其模是a的模的3倍，即
|3a| = 3|a| ．
数与向量的乘法运算叫做向量的数乘运算，容易验证，对于
请画出图形来，分别验证这些法则．
因为O分别为AC，BD的中点，所以
向量的加法、减法、数乘运算都叫做向量的线性运算．
（1）3(a − 2 b) − 2(2 a＋b)；
（2）3 a − 2(3 a − 4 b)＋3(a − b)．
（1） − a − 8b ；（2）5b ．