高教版（中职）拓展模块2.2.2 双曲线的性质教课课件ppt

这是一份高教版（中职）拓展模块2.2.2 双曲线的性质教课课件ppt，共9页。PPT课件主要包含了想想双曲线怎样画，两个焦点间距离叫做，这两个定点叫做，双曲线，双曲线的焦点，双曲线的焦距，小于F1F2，焦点在y轴上等内容，欢迎下载使用。

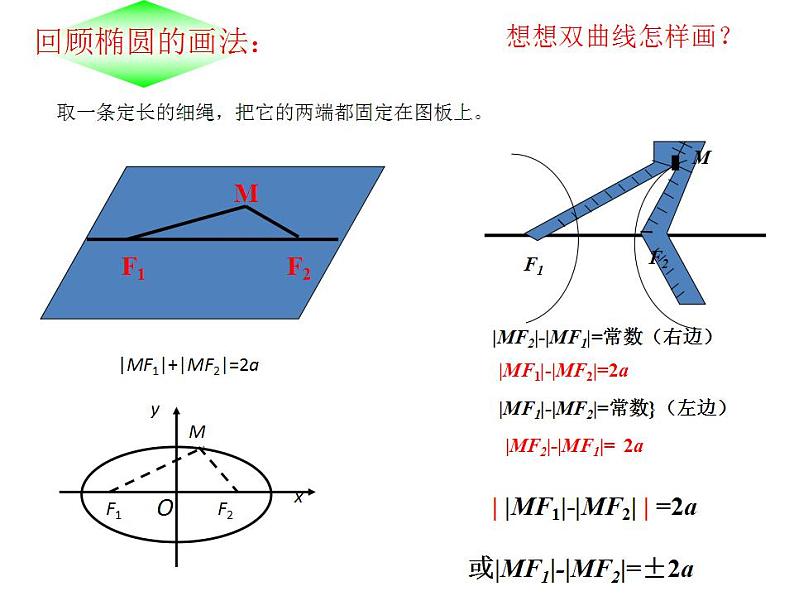
取一条定长的细绳，把它的两端都固定在图板上。
|MF1|+|MF2|=2a
|MF1|-|MF2|=2a
|MF2|-|MF1|=常数（右边）
|MF1|-|MF2|=常数}（左边）
| |MF1|-|MF2| | =2a
|MF2|-|MF1|=
或|MF1|-|MF2|=±2a
1. 双曲线的定义：我们把平面内与两个定点F1，F2的距离的差的绝对值等于常数（小于|F1F2|）的点的轨迹叫做
即： 2a ＞2c （ a ＞c）
2.推导双曲线标准
由定义可知，双曲线就是集合P={M||MF1|-|MF2|=2a}.因为|MF1|= ， |MF2|= ，所以类比建立椭圆标准方程的化简过程，化简①，得(c2-a2)x2-a2y2=a2(c2-a2),两边同除以(c2-a2），得
由双曲线的定义可知2c>2a，即c>a所以c2-a2>0.类比椭圆标准方程的建立过程，
我们令c2-a2=b2，其中b>0 ，代入上式，得
（其中b2=c2-a2 且a不一定比b大）
双曲线的标准方程：焦点在x轴上：
已知双曲线两个焦点分别为F1(-5,0)F2(5,0)，双曲线上的一点P到F1,F2的距离差的绝对值等于6，求双曲线的标准方程.
解：因为双曲线的焦点在 x轴上，所以设它的标准方程为因为2a=6，2c=10，所以 a=3，c=5，所以 b2=52-32=16.因此，双曲线的标准方程：