高中数学高教版（中职）基础模块下册第10章 概率与统计初步10.2 概率10.2.3 古典概型教学设计及反思

这是一份高中数学高教版（中职）基础模块下册第10章 概率与统计初步10.2 概率10.2.3 古典概型教学设计及反思，共6页。教案主要包含了引入新课，小结与提问，课外作业等内容，欢迎下载使用。
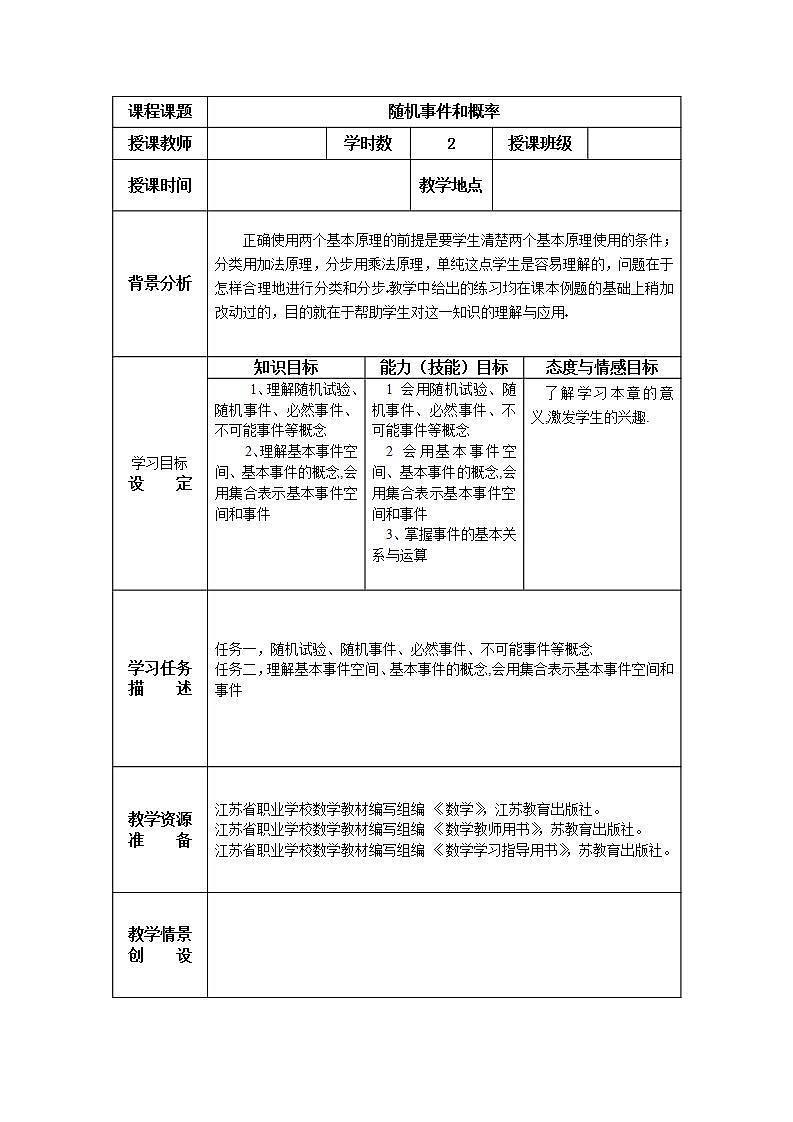
课程课题随机事件和概率授课教师 学时数2授课班级 授课时间 教学地点 背景分析正确使用两个基本原理的前提是要学生清楚两个基本原理使用的条件；分类用加法原理，分步用乘法原理，单纯这点学生是容易理解的，问题在于怎样合理地进行分类和分步教学中给出的练习均在课本例题的基础上稍加改动过的，目的就在于帮助学生对这一知识的理解与应用 学习目标设    定知识目标能力（技能）目标态度与情感目标1、理解随机试验、随机事件、必然事件、不可能事件等概念   2、理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件 1 会用随机试验、随机事件、必然事件、不可能事件等概念2 会用基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件3、掌握事件的基本关系与运算 了解学习本章的意义,激发学生的兴趣. 学习任务描    述  任务一，随机试验、随机事件、必然事件、不可能事件等概念任务二，理解基本事件空间、基本事件的概念,会用集合表示基本事件空间和事件   教学资源准    备 江苏省职业学校数学教材编写组编 《数学》，江苏教育出版社。江苏省职业学校数学教材编写组编 《数学教师用书》，苏教育出版社。江苏省职业学校数学教材编写组编 《数学学习指导用书》，苏教育出版社。 教学情景创    设  一 引入新课一、概率论研究的对象1、两类现象---确定现象与不确定现象先从实例来看自然界和社会上存在着两类不同的现象。例1、水在一个大气压力下,加热到100℃就沸腾。例2、向上抛掷一个五分硬币,往下掉。例3、太阳从东方升起。例4、一个大气压力下,20℃的水结冰。例1,例2,例3是必然发生的,而例4是必然不发生的。条件完全决定结果的现象称之为确定性现象或必然现象.微积分,线性代数等就研究必然现象的数学工具.与此同时,在自然界和人类社会中,人们还发现具有不同性质的另一类现象先看下面实例。例5、用大炮轰击某一目标,可能击中,也可能击不中。例6、在相同的条件下,抛一枚质地均匀的硬币,其结果可能是正面(我们常把有币值的一面称作正面)朝上,也可能是反面朝上。例7、次品率为50%的产品,任取一个可能是正品,也可能是次品。例8、次品率为1%的产品,任取一个可能是正品,也可能是正品。      例5~例8这类现象归纳起来可以看作在相同条件下一系列的试验或观察,而每次试验或观察的可能结果不止一个,在每次试验或观察之前无法预知确切结果,即呈现出不确定性(即这些现象的结果事先不能完全确定)。条件不能完全决定结果的现象称之为不确定性现象或偶然现象,也称之为随机现象。2、统计规律性、概率论研究的对象      对于不确定性现象,人们经过长时期的观察或实践的结果表明,这些现象并非是杂乱无章的,而是有规律可寻的.例如,大量重复抛一枚硬币,得正面朝上的次数与正面朝下的次数大致都是抛掷总次数的一半.在大量地重复试验或观察中所呈现出的固有规律性,就是我们以后所说的统计规律性.而概率论正是研究这种随机(偶然)现象,寻找他们的内在的统计规律性的一门数学学科。       概率论是数理统计的基础,由于随机现象的普遍性,使得概率与数理统计具有及其广泛的应用。另一方面,广泛的应用也促进概率论有了极大的发展。二、随机试验    对随机现象进行的试验或观察称为随机试验,简称试验,它具有下列特性(征)：（1）试验可以在相同条件下重复进行；（2）试验的所有可能结果是明确可知的,并且不止一个；（3）每次试验总是恰好出现这些可能结果中的一个,但在一次试验之前不能肯定这次试验会出现哪一个结果。随机实验记为E.例1、E1:投掷一枚硬币,观察正反面朝上的情况。它有两种可能的结果就是“正面朝上”或“反面朝上”,投掷之前不能预言哪一个结果出现，且这个试验可以在相同的条件下重复进行，所以E1是一个随机试验。例2、E2：掷一颗骰子，观察出现的点数。它有6种可能的结果就是“出现1点”，“出现2点”•••，“出现6点”。但在投掷之前不能预言哪一个结果出现，且这个试验可以在相同的条件下重复进行，所以E2是一个随机试验。例3、E3：在一批灯泡中任意抽取一只，测试他的寿命。我们知道灯泡的寿命（以小时计）t≥0,但在测试之前不能确定它的寿命有多长，这一试验也可以在相同的条件下重复进行，所以E3是一个随机试验。三、基本事件空间、随机事件对随机试验我们感兴趣的是试验结果。随机试验E的每一个可能的结果，称之为基本事件，它是不能再分的最简单的事件。因为随机试验的所有结果是明确的，从而所有的基本事件也是明确的，我们把随机试验E的所有基本事件所组成的集合（全体）叫做试验E的基本事件空间，通常用字母Ω表示，Ω中的点，即基本事件。有时也称做样本点，常用ω表示。例4、试验E2：投掷一枚硬币。“正面朝上”和“反面朝上”是E1的基本事件，所以基本事件空间Ω={正，反}。例5、试验E2：掷一颗骰子。         令i表示“出现i点”。（i=1，2，•••，6），是E2的基本事件，所以基本事件空间Ω={1，2，•••，8}。例6、试验E3：测试灯泡寿命。         令t表示“测得灯泡寿命为t小时”，则0≤t＜+∞是E3的基本事件，所以Ω={t|0≤t＜+∞}.例7、一个盒子中有十个相同的球，但5个是白色的，另外5个是黑色的，搅匀后从中任意摸取一球。令ω1={取得白球}，ω2={取得黑球}，则Ω={ω1，ω2}。例8、试验E4：将一硬币抛掷两次。则Ω={（正，正），（正，反），（反，正），（反，反）}。其中（正，正）表示“第一次正面朝上，第二次正面朝上”，余类推。                                                                                                        例9、个盒子中有十个完全相同的球，分别标以号码1，2，•••，10，从中任取一球，令i={取得球的标号为i},则Ω={1，2，•••，10}。                                                在随机试验中，有时关心的是带有某些特征的基本事件是否发生。如在例5中E2试验，我们可以研究      A表示“出现2点”即A={出现2点}      B表示“出现偶数点”      C表示“出现的点数≤4”这些结果是否发生？          在例9中，我们可以研究                    D={球的标号=6}           E={球的标号是偶数}           F={球的标号≤5}这些结果是否发生？    其中A是一个基本事件，而B是由{出现2点}，{出现4点}和{出现6点}这三个基本事件组成的，当且仅当这三个基本事件中有一个发生，B发生。所以B，C，E，F是由若干个有某些特征的基本事件所组成的，相对与基本事件，就称她们是复合事件。无论是基本事件还是复合事件，它们在试验中发生与否，都带有随机性，所以都叫随机事件或简称事件，今后我们常用大写字母A，B，C等表示事件。    我们已经知道基本事件空间Ω包含了全体基本事件，而任一随机事件不过是有某些特征的基本事件所组成，所以从集合论的观点来看，任一随机事件不过是基本事件空间Ω的一个子集而已，而且它发生，当且仅当它中的一个样本点发生。如在例5中，随机事件A、B、C都是Ω的子集，它们可以简单地表示为                 Ω={1，2，3，4，5，6}                 A={2}，B={2，4，6}                 C={1，2，3，4}在例9中                 Ω={1，2，•••，10}                 D={6}，E={2，4，5，8，10}                 F={1，2，3，4，5}     事件D只含一个试验结果，而在事件E和F中各含5个可能的试验结果。所以我们也可以这样说，只包含一个试验结果的事件为基本事件，由两个或两个以上基本事件复合而成的事件为复合事件。     在试验E中必然会发生的事情叫必然事件，不可能发生的事情叫不可能事件，例如例5E2中“点数不大于6”是必然事件，“点数大于6”是不可能事件，因为Ω是所有基本事件所组成的，因而在任一次试验中，必然要出现Ω中的某一基本事件ω，即ω∈Ω。也就是在试验中，Ω必然会发生，所以今后用Ω来代表必然事件，类似地，空集Φ可以看作是Ω的子集，它在任一次试验中都不会发生，所以Φ是不可能事件。必然事件和不可能事件的发生与否，已经失去了今后研究的方便，我们把它们当作一种特殊的随机事件。     小结  将随机事件表示成由样本点组成的集合，就可以将事件间的关系和运算归结为集合之间的关系和运算，这不仅对研究事件的关系和运算是方便的，而且对研究随机事件发生的可能性大小的数量指标—概率的运算也是非常有益的。四、事件之间的关系和运算    一个基本事件空间Ω中，可以有很多的随机事件。概率论的任务之一，是研究随机事件的规律，通过对简单事件规律的研究去掌握更复杂事件的规律。为此，下面我们引进事件之间的一些重要关系和运算，通过研究事件间的各种关系，进而研究事件间的概率的各种关系，就有可能利用较简单事件的概率去推算较复杂的事件的概率。    在以下的叙述中，设试验E的基本事件空间为Ω，还给了Ω中的一些事件，如A，B，A(=1,2,•••)等等。（一）事件的包含及相等当事件A发生时必然导致事件B发生，则称A包含于B或B包含A，记为A或B。即，用文（Venn）图表示为：反之，B若B不发生，则必然A也不会发生。显然，对任意事件A有：⑴A；⑵；⑶若A，B，则A。比如在例5中，A={2}，B={2，4，6}，显然AB。如果将事件用集合表示，则事件B包含事件A即为A是B的子集合（B包含集合A）。如果有AB且BA，则称事件A与事件B相等，记作A=B。易知，相等的两个事件A、B，总是同时发生或同时不发生，亦即A=B等价于它们是由相同的试验结果构成的。如在例9中，若A={球的标号为偶数}，B={球的标号为2、4、6、8、10}，则显然有A=B，所谓A=B，就是A、B中含有相同的样本点。显然有A＝BA且B（二）事件的互不相容如果事件A与事件B不能同时发生，也就是说AB是一个不可能事件，即AB=Ф，则称二事件A与B是互不相容的（或互斥的）。A，B互不相容等价于它们不包含相同的试验结果。互不相容事件A与B没有公共的样本点。用文（Venn）图表示为：     若用集合表示事件，则A，B互不相容即为A与B是不交的。    如果n个事件A1，A2，…，An中，任意两个事件不可能同时发生，即AiAj=Ф(1≤i＜j≤n)，则称这n个事件A1，A2，…An是互不相容的（或互斥的）。在任意一个随机试验中基本事件都是互不相容的。还容易看出，事件A与B-A是互不相容的。（三）对立事件    若A是一个事件，令=Ω-A，称是A的对立事件或逆事件。容易知道，在一次试验中，若A发生，则必不发生（反之亦然），即A与中必然有一个发生，且仅有一个发生，即事件A与满足条件A=Ф，A∪=Ω。由所有不包含在A中的试验结果构成。即，用文（Venn）图表示为：比如例5中，A={2，4，6}，B={1，3，5}，则=B，=A，所以A，B互为对立事件。必然事件与不可能事件也是互为对立事件。显然有：（证明：）    注：互逆事件与互斥事件的区别：互逆必定互斥，互斥不一定互逆；互逆只在样本空间只有两个事件时存在，互斥还可在样本空间有多个事件时存在。例如，在抛硬币的试验中，设A={出现正面}，B={出现反面}，则A与B互斥且A与B互为对立事件；而在掷骰子的试验中，设A={出现1点}，B={出现2点}，则A与B互斥，但A与B不是对立事件。    由事件关系的定义看出，它与集合的关系是一致的，因此集合的运算性质对事件的运算也都适用。（四）事件的运算法则：1、交换律       A∪B=B∪A，AB=BA。2、结合律       A∪B∪C=A∪(B∪C)=(A∪B) ∪C       ABC=(AB)C=A(BC)3、分配律       A(B∪C)=AB∪AC       A∪BC=(A∪B)(A∪C)     例10、掷一颗骰子的试验，观察出现的点数：事件A表示“奇数点”；B表示“点数小于5”；C表示“小于5的偶数点”。用集合的列举法表示下列事件：Ω，A，B，C，A∪B，A-B，AB，AC，C-A，      解           Ω={1，2，3，4，5，6}                   A={1，3，5}                   B={1，2，3，4}                   C={2，4}                   A∪B={1，2，3，4，5}A-B={5}AB={1，3}AC=ФC-A={2，4}={1，2，3，4，6}例11、设A，B，C是三事件，用A，B，C的运算关系表示下列事件：（1）B，C都发生，而A不发生。（2）A，B，C中至少有一个发生。A∪B∪C（3）A，B，C中恰有一个发生。（4）A，B，C中恰有两个发生。（5）A，B，C中不多于一个发生。（6）A，B，C中不多于二个发生。二 小结与提问：   本节课介绍了随机试验、随机事件、基本事件空间等概念，在此基础上讨论了事件之间的各种关系与运算。由事件间的关系与运算，一个复合事件的表示方式是否一定是唯一的？三 课外作业：  1 书上 2 练习册