初中1 全等三角形优秀精练

13.2.1全等三角形同步练习华师大版初中数学八年级上册

一、选择题（本大题共12小题，共36.0分）

1. 已知≌，且的周长为6，则的周长为

A. 12 B. 10 C. 8 D. 6

2. 如图，N，C，A三点在同一直线上，在中，：：：5：10，又≌，则：等于

A. 1：2 B. 1：3 C. 2：3 D. 1：4

3. 如图所示，≌，，，BC的延长线交DA于点F，交DE于点G，，，，则的度数为    

A.
B.
C.
D.

4. 如图，已知，则下列结论：
    
    ，；，；，．
   其中正确的是   

A.  B.  C.  D.

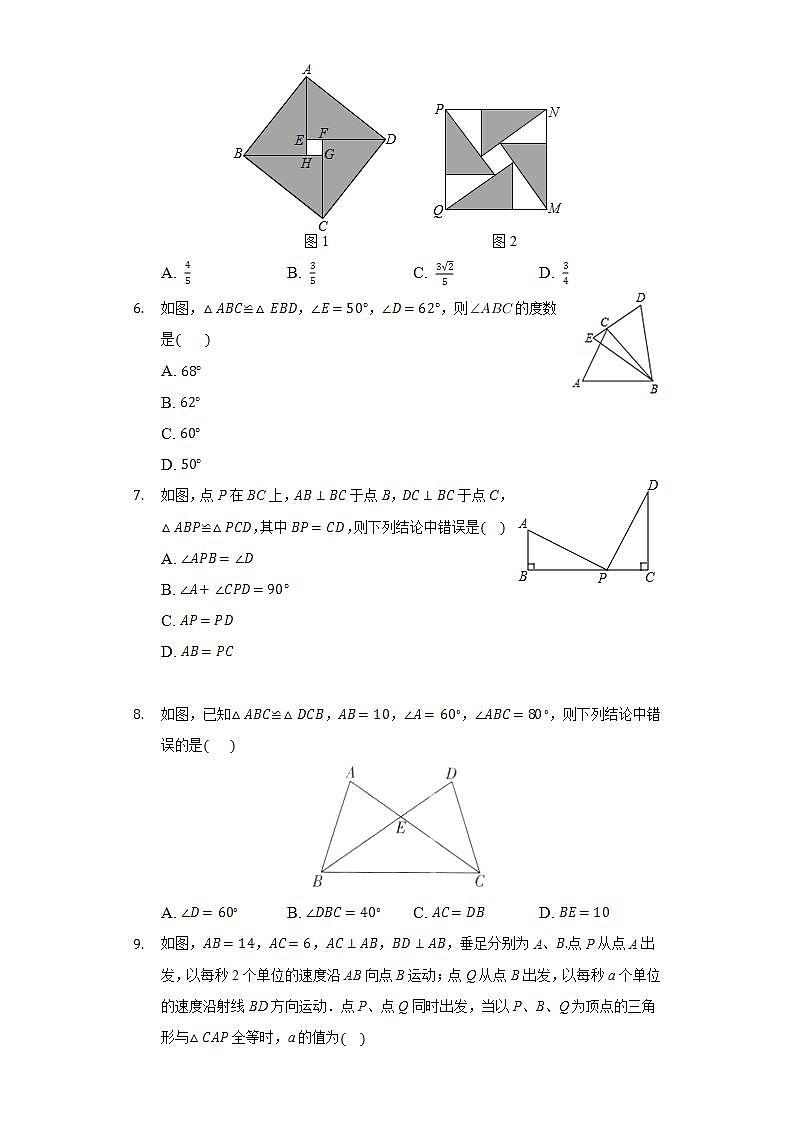
5. 如图1是2002年北京国际数学家大会徽标图案，它是由4个全等的直角三角形和一个小正方形组成．把这4个全等直角三角形进行如图2的摆放，得到一个大正方形PQMN，若，，则为

A.  B.  C.  D.

6. 如图，，，，则的度数是     

A.
B.
C.
D.

7. 如图，点P在BC上，于点B，于点C，≌，其中，则下列结论中错误是

A.
B.
C.
D.
 

8. 如图，已知，，，，则下列结论中错误的是   

A.  B.  C.  D.

9. 如图，，，，，垂足分别为A、点P从点A出发，以每秒2个单位的速度沿AB向点B运动；点Q从点B出发，以每秒a个单位的速度沿射线BD方向运动．点P、点Q同时出发，当以P、B、Q为顶点的三角形与全等时，a的值为

A. 2 B. 3 C. 2或3 D. 2或

10. 下列说法：周长相等的两个三角形是全等三角形；
    周长相等的两个圆是全等图形；
    如果两个三角形是全等三角形，那么这两个三角形的面积相等；
    所有的正方形是全等图形；
    在中，当，时，这个三角形是直角三角形．
    正确的有     

A. 1个 B. 2个 C. 3个 D. 4个

11. 如图所示，≌，如果，，，那么BC的长为

A. 6cm B. 4cm C. 7cm D. 不能确定

12. 已知，且，，则EF的长不可能是   

A. 2 B. 3 C. 4 D. 5

二、填空题（本大题共5小题，共15.0分）

13. 已知有两个三角形全等，若一一个三角形三边的长分别为3、5、7，另一个三角形三边的长分别为3、、，则          ．
14. ，若的面积为15，BC边上的高为5，则__________．
15. 如图，于点A，，，射线于点B，一动点E从A点出发以2个单位秒沿射线AB运动，点D为射线BM上一动点，随着E点运动而运动，且始终保持，若点E经过t秒，与全等，则t的值为______秒．
16. 如图，已知四边形ABCD中，厘米，厘米，厘米，，点E为AB的中点．如果点P在线段BC上以3厘米秒的速度由B点向C点运动，同时，点Q在线段CD上由C点向D点运动．当点Q的运动速度为______时，能够使与全等．
17. 如图，，于A，于B，且，P点从B向A运动，每分钟走1m，Q点从B向D运动，每分钟走2m，P、Q两点同时出发，运动________分钟后与全等．
    
     

三、解答题（本大题共6小题，共48.0分）

18. 如图，在中，点D，E分别是边BC，AB上的点，若，求的度数．

19. 如图，≌，，，，点C为AD中点．求的度数和AE的长．

20. 如图，点A、B、C在同一直线上，点E在BD上，且，，．
     

求DE的长；

判断AC与BD的位置关系，并说明理由．

判断直线AD与直线CE的位置关系，并说明理由．






 

21. 如图，已知，与是对应角，点F，H，G，M在同一直线上．
    
     

写出图中相等的线段与角

若，，，求MN和HG的长．






 

22. 如图所示，已知≌，，．
    求证：．
    求AB的长．

23. 如图，已知≌，点E在AB上，DE与AC相交于点F．
    当，时，求线段AE的长；
    已知，，求与的度数．
    
     

答案和解析

1.【答案】D
 

【解析】解：≌，且的周长为6，
的周长为6，
故选：D．
根据全等三角形的周长相等，判断即可．
本题考查全等三角形的性质，解题的关键是掌握全等三角形的性质，属于中考常考题型．
 

2.【答案】D
 

【解析】

【分析】
本题考查了全等三角形的性质；利用三角形的三角的比，求得三个角的大小是很重要的方法，要注意掌握．利用三角形的三角的比，求出三角的度数，再进一步根据各角之间的关系求出、的度数可求出结果．
【解答】
解：在中，：：：5：10
设，则，

解得
则，，

又≌


：：：4
故选D  

3.【答案】B
 

【解析】

【分析】
本题考查了全等三角形的性质，三角形的内角和定理，邻补角的定义，解题关键在于熟记性质并准确识图．

根据全等三角形对应角相等可得，，再根据邻补角的定义求出，然后根据三角形的内角和定理列出方程求解即可．

【解答】

解：≌，，，，，
，
由三角形的内角和定理得，，
，解得．

故选：B．

4.【答案】D
 

【解析】

【分析】
本题考查全等三角形的性质，平行线的判定，根据全等三角形的性质对进行判定，根据内错角相等，两直线平行对进行判定即可．
【解答】
解：，
，
，，
故正确；
而，，
又，，
故正确
因此正确的是，
故选D．  

5.【答案】A
 

【解析】解：如图1中，设，
在中，，
，
或．
，，
如图2中，

由∽，可得，
，
，
，
，
故选：A．
如图1中，设，在中，，利用勾股定理求出x，再在图2中，利用相似三角形的性质求出PQ可得结论．
本题考查全等三角形的性质，正方形的性质，勾股定理，相似三角形的判定和性质等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．
 

6.【答案】A
 

【解析】分析
本题主要考查了全等三角形的性质，此题比较简单，掌握好全等三角形的知识是解题关键．
由全等可以得到，，再由三角形内角和定理即可求出．
解答
解：，
，
，，
，
．
故选A．
 

7.【答案】B
 

【解析】

【分析】
本题考查的是全等三角形的性质，掌握全等三角形的对应边和对应角相等是解题的关键．
根据全等三角形的性质解答即可．
【解答】
解：≌，
，，，，
是错误的，
故选B．  

8.【答案】D
 

【解析】 ，，

，

，

，，，

，B，C结论正确，

由已知不能得出，结论错误故选D．

9.【答案】D
 

【解析】解：当≌时，则，，
，，
，，
，
，
解得；
当≌时，则，，．
，，
，，
，
解得；
由上可得a的值是2或，
故选：D．
根据题意，可以分两种情况讨论，第一种≌，第二种≌，然后分别求出相应的a的值即可．
本题考查全等三角形的性质，解答本题的关键是明确有两种情况，利用数形结合的思想解答．
 

10.【答案】B
 

【解析】分析
本题主要考查了全等图形的定义以及三角形的内角和定理，熟练掌握这些知识是解题的关键，根据这些知识对各小题分析判断即可得解．
详解
解：周长相等的两个三角形不一定是全等三角形，如边长为3、4、5和边长4、4、4的三角形的周长相等但不全等，故错误； 
如果两个圆的周长相等，那么这两个圆的半径相等，则这两个圆是全等图形，故正确；
如果两个三角形是全等三角形，那么这两个三角形的面积相等，故正确；
所有的正方形边长不一定相等，所以不一定是全等图形，故错误；
当，时，，
，
，
这个三角形不是直角三角形，故错误．
综上所述，正确的是．
故选B．
 

11.【答案】B
 

【解析】解：≌，
，
，
，
故选B．
根据全等三角形的性质得出，代入求出即可．
本题考查了全等三角形的性质的应用，解此题的关键是能根据全等三角形的性质得出，注意：全等三角形的对应边相等，对应角相等．
 

12.【答案】D
 

【解析】，且，，

，，

即，

所以EF的长不可能是故选D．

13.【答案】5或4
 

【解析】 两个三角形全等，
，或，，
，或，，
或，
故答案为5或4．
 

14.【答案】6
 

【解析】

【分析】
本题考查了全等三角形的性质和三角形的面积，注意：全等三角形的对应边相等，对应角相等，且两三角形的面积也相等．根据全等三角形性质得出，根据三角形的面积公式即可求出答案．
【解答】
解：，
，

，
，
．

15.【答案】2，6，8
 

【解析】解：当E在线段AB上，时，≌，
，
，
，
点E的运动时间为秒；

当E在BN上，时，
，
，
，
点E的运动时间为秒；

当E在BN上，时，≌，
，
点E的运动时间为秒，
故答案为：2，6，8．
此题要分两种情况：当E在线段AB上时，当E在BN上，再分别分成两种情况，进行计算即可．
本题考查三角形全等的性质，熟练掌握全等三角形的对应边相等是解题的关键．
 

16.【答案】3厘米秒或厘米秒
 

【解析】

【分析】
本题考查了全等三角形的性质和判定的应用，解决问题的关键是掌握全等三角形的对应边相等，属于中档题．
分两种情况讨论，依据全等三角形的对应边相等，即可得到点Q的运动速度．
【解答】
解：设点P运动的时间为t秒，则，，
，
当，时，与全等，
此时，，
解得，
，
此时，点Q的运动速度为厘米秒；
当，时，与全等，
此时，，
解得，
点Q的运动速度为厘米秒；
故答案为3厘米秒或厘米秒．  

17.【答案】3
 

【解析】解：于A，于B，
，
设运动x分钟后与全等；
则，，则，
分两种情况：
若，则，
若，则，
解得：，
此时与不全等；
综上所述：运动3分钟后与全等．
故答案为：3．
由全等三角形的性质可得到，然后依据时间路程速度求解即可．
本题主要考查的是全等三角形的性质，依据题意得是解题的关键．
 

18.【答案】解：，，
，B.
，
，B.
 ．
．
．
 

【解析】见答案
 

19.【答案】解：≌，，，
，，，，
，
，
，
，
点C为AD中点，
，
．
 

【解析】本题考查的是全等三角形的性质、三角形内角和定理等，掌握全等三角形的对应边相等、对应角相等是解题的关键．根据全等三角形的性质求出，AD，根据三角形内角和定理求出，根据周角的概念求出，根据C为AD中点求出AE．
 

20.【答案】≌，
，．
．
与AC垂直理由：
≌，
．
又点A、B、C在一条直线上，
．
与AC垂直．
直线AD与直线CE垂直．
理由：如图，延长CE交AD于点F．

≌，
，
在中，
，
，
，
，即．
 

【解析】本题考查全等三角形的性质和垂线的概念和性质，关键是确定全等三角形的对应角．
根据全等三角形的性质得出，，便可得出结果；
根据全等三角形的性质得出，又点A、B、C在一条直线上，得出，便可得出结果；
延长CE交AD于点F，根据全等三角形的性质得出，然后得出，得出，便可得出结果．
 

21.【答案】解：相等的线段：，，，．

相等的角：，，，．

，，
．

，，，，

．

【解析】见答案．
 

22.【答案】证明：≌，
．
．
≌，
．
．
．
，



 

【解析】根据全等三角形的性质和平行线的判定解答即可；
根据全等三角形的性质解答即可．
此题考查全等三角形的性质，关键是根据全等三角形的对应角相等和对应边相等解答．
 

23.【答案】解：≌，，，
，，
；
≌，，，
，，，
，
，
，
，
，
．
 

【解析】根据全等三角形的性质得到，，结合图形计算，得到答案；
根据全等三角形的性质得到，，根据三角形内角和定理求出，计算即可．
本题考查了全等三角形的性质，三角形的内角和定理，三角形外角的性质，熟练掌握全等三角形的性质是解题的关键．