初中数学华师大版七年级下册10.1 轴对称综合与测试综合训练题

这是一份初中数学华师大版七年级下册10.1 轴对称综合与测试综合训练题，共18页。试卷主要包含了0分），【答案】A，【答案】B，【答案】D等内容，欢迎下载使用。
 10.1轴对称同步练习华师大版初中数学七年级下册一、选择题（本大题共12小题，共36.0分）如图，在直角三角形ABC中，，，，垂足为D，与关于直线AD对称，点B的对称点是点，则的度数为    A.  B.  C.  D. 如图，在的正方形的网格中，格线的交点称为格点，以格点为顶点的三角形称为格点三角形，图中的为格点三角形，在图中最多能画出个格点三角形与成轴对称．A. 6个
B. 5个
C. 4个
D. 3个如图的的正方形网格中，的顶点都在小的格点上，这样的三角形称为格点三角形，在网格中与成轴对称的格点三角形一共有       
A. 2个 B. 3个 C. 4个 D. 5个如图，在中，AD是的对称轴，P是AD上一个动点，E是AB边上的一个定点，则下列线段的长度等于最小值的是A. BC    
B. CE    
C. AD    
D. AC在下列“禁毒”“和平”“志愿者”“节水”这四个标志中，属于轴对称图形的是   A.  B.  C.  D. 下列说法：轴对称图形只有一条对称轴；两个图形成轴对称，这两个图形是全等图形；全等的两个图形一定成轴对称；轴对称图形指一个图形，而成轴对称是对两个图形而言的．其中正确的个数是    A. 1 B. 2 C. 3 D. 4如图，由4个小正方形组成的方格中，的顶点都在格点上，在这个方格中再画出一个三角形，使它的顶点都在格点上，且与关于某条直线成轴对称，这样的三角形共有    A. 1个
B. 2个
C. 3个
D. 4个如图，由4个小正方形组成的田字格，的顶点都是小正方形的顶点，在田字格上能画出与成轴对称，且顶点都在小正方形顶点上的三角形的个数共有A. 2个
B. 3个
C. 4个
D. 5个下列四个图形中，不是轴对称图形的是 A.  B.
C.  D. 如图，四边形ABCD中，，，在BC、CD上分别找一点M、N，使周长最小时，则的度数为
A.  B.  C.  D. 如图，，点P为内一点，点M、N分别在OA、OB上，当周长最小时，的度数是A.
B.
C.
D. 将一张长方形纸片按以下过程操作：
步骤在CD上取一点P，将角C向下翻折，使点C的对称点落在原长方形所在的平面内，这样形成折痕PM，如图步骤将角D向上翻折，使点D的对称点落在所在的直线上，得到折痕PN，如图，则的度数为   
A.  B.  C.  D. 二、填空题（本大题共6小题，共18.0分）如图，中，，，，点P为AC边上的动点，过点P作于点D，则的最小值为______．

  如图，把一张长方形的纸按图那样折叠后，B、D两点落在、点处，若得，则的度数为____．

 小明放假去外地看爷爷，他买的是11点的火车，由于去得早，小明不小心在候车室睡着了，等他醒来的时候，他从镜子中看到背面墙上的电子钟上显示的时间如图所示，他吓了一身汗，以为自己错过了火车，同学们，小明到底能不能赶上11点的火车呢小明醒来时的正确时间是          ．
 在正方形网格中，已有3个小方格涂黑，要从13个白色小方格中选出一个也涂黑，使所有黑色部分组成的图形为轴对称图形，这样的白色小方格有________个．

  如图，在四边形ABDE中，C是BD边的中点，，，，若，则线段AE长度的最大值是______．
如图所示是某时刻在镜子中看到准确时钟的情况，则实际时间是________．


   三、解答题（本大题共5小题，共40.0分）如图，在正方形网格上有一个．在图中画出关于直线MN对称的图形不写画法若网格上的每个小正方形的边长为2，求出的面积．






 如图，已知四边形ABCD与四边形EFGH关于直线MN对称，，，，．试写出EF，AD的长度求的度数连结BF，线段BF与直线MN有什么关系






 如图，要在街道旁修建一个牛奶站，向居民区A，B提供牛奶，牛奶站建在什么地方，才能使居民区A，B到它的距离之和最短







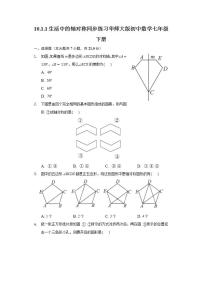
 如图，网格中的与为轴对称图形．
利用网格线作出与的对称轴l；
结合所画图形，在直线l上画出点P，使最小；
如果每一个小正方形的边长为1，请直接写出的面积______．







 先阅读下列一段文字，再解答问题．已知在平面内有两点，，其两点间的距离公式为，同时，当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时，两点间距离公式可简化为或已知点，，试求A，B两点间的距离；已知点A，B在平行于x轴的直线上，点A的横坐标为6，点B的横坐标为，试求A，B两点间的距离；应用平面内两点间的距离公式，求代数式的最小值．







答案和解析1.【答案】A
 【解析】略
 2.【答案】A
 【解析】【分析】
本题考查了利用轴对称变换作图，熟练掌握网格结构并准确找出对应点的位置是解题的关键，本题难点在于确定出不同的对称轴．
根据网格结构分别确定出不同的对称轴，然后作出轴对称三角形即可得解．
【解答】
解：如图，最多能画出6个格点三角形与成轴对称．

故选A．  3.【答案】B
 【解析】【分析】
本题考查了轴对称的性质，难点在于确定出对称轴的不同位置．
【解答】
解：如图所示，对称轴有三种位置，与成轴对称的格点三角形有3个．

故选B．  4.【答案】B
 【解析】【分析】
本题考查轴对称最短问题，轴对称的性质，解题的关键是灵活运用所学知识解决问题．连接PC，只要证明，即可推出，由，推出P、C、E共线时，的值最小，最小值为CE的长度．
【解答】
解：如图，连接PC，

是的对称轴
点C是点B关于直线AD的对称点，
，
，
，
、C、E共线时，的值最小，最小值为CE的长度。
故选：B．  5.【答案】B
 【解析】【分析】
本题主要考查的是轴对称图形。根据轴对称图形的概念求解。如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴。
【解答】
解：不是轴对称图形，故A不符合题意；
B.是轴对称图形，故B符合题意；
C.不是轴对称图形，故C不符合题意；
D.不是轴对称图形，故D不符合题意。
故选B。  6.【答案】B
 【解析】【分析】
本题考查了轴对称图形的知识，解答本题的关键是掌握轴对称图形的概念和轴对称的性质．根据轴对称图形的概念和轴对称的性质结合题目中的说法求解．
【解答】
解：轴对称图形不一定只有一条对称轴，故原说法错误；
两个图形成轴对称，这两个图形是全等图形，该说法正确；
全等的两个图形不一定成轴对称，故原说法错误；
轴对称图形是指一个图形，而轴对称是指两个图形而言，该说法正确．
则正确的有共2个．
故选：B．  7.【答案】D
 【解析】【分析】
此题考查了利用轴对称涉及图案的知识，关键是根据要求顶点在格点上寻找对称轴，有一定难度，注意不要漏解因为顶点都在小正方形上，故可分别以大正方形的两条对角线AB、EF及MN、CH为对称轴进行寻找．
【解答】
解：分别以大正方形的两条对角线AB、EF及MN、CH为对称轴，作轴对称图形：
则、、、都是符合题意的三角形，
故选：D．  8.【答案】C
 【解析】【分析】
此题考查了利用轴对称涉及图案的知识，关键是根据要求顶点在格点上寻找对称轴，有一定难度，注意不要漏解．
因为顶点都在小正方形上，故可分别以大正方形的两条对角线AB、EF及MN、CH为对称轴进行寻找．
【解答】
解：分别以大正方形的两条对角线AB、EF及MN、CH为对称轴，作轴对称图形：

则、、、都是符合题意的三角形．
故选：C．  9.【答案】B
 【解析】【分析】
本题主要考查轴对称图形，可根据轴对称图形的定义进行判断求解。
【解答】
解：A选项，是轴对称图形，故错误；
B选项，不是轴对称图形，故正确；
C选项，是轴对称图形，故错误；
D选项，是轴对称图形，故错误。
故选B。  10.【答案】B
 【解析】【分析】
根据要使的周长最小，即利用点的对称，让三角形的三边在同一直线上，作出A关于BC和CD的对称点，，即可得出，进而得出
【解答】
解：如图，作A关于BC和CD的对称点，，连接，交BC于M，交CD于N，

则即为的周长最小值


，
且，


故选B。  11.【答案】B
 【解析】解：分别作点P关于OA、OB的对称点、，连接、交OA于M，交OB于N，
，，，
根据轴对称的性质可得，，
的周长的最小值，
由轴对称的性质可得，
等腰中，，
，
故选：B．
分别作点P关于OA、OB的对称点、，连接、交OA于M，交OB于N，的周长最小值等于的长，然后依据等腰中，，即可得出．
本题考查了轴对称最短路线问题，正确作出辅助线得到等腰中的度数是关键．凡是涉及最短距离的问题，一般要考虑线段的性质定理，多数情况要作点关于某直线的对称点．
 12.【答案】B
 【解析】根据对折的特点，知，，所以．
 13.【答案】
 【解析】解：如图，作点B关于AC的对称点，
过点作于点D，交AC于点P，
点P即为所求作的点，此时有最小值，
连接，根据对称性的性质，
，
在中，，，，
，
，，，
≌，
，
即，
，
．
故答案为：．
作点B关于AC的对称点，过点作于点D，交AC于点P，点P即为所求作的点，此时有最小值，连接，根据对称性的性质，，证明≌，根据，即可求出的最小值．
本题考查了轴对称最短路线问题，解决本题的关键是掌握轴对称的性质．
 14.【答案】
 【解析】【分析】
本题考查轴对称的性质，在解答此类问题时要注意数形结合的应用．根据轴对称的性质可得，再根据，可得出的度数．
【解答】
解：根据轴对称的性质得：，
又，
可得，
．
故答案为．  15.【答案】
 【解析】略
 16.【答案】4
 【解析】【分析】
此题利用格点图，考查学生轴对称性的认识．此题关键是找对称轴，按对称轴的不同位置，找出第4个小正方形所在位置．根据轴对称图形的概念分别找出各个能成轴对称图形的小方格即可．
【解答】
解：如图所示，有4个位置使之成为轴对称图形．

故答案为4．  17.【答案】14
 【解析】解：作B关于AC的对称点F，D关于EC的对称点G，连接AF，FC，CG，EG，FG，如图所示：

是BD边的中点，
，
≌，
，
．
同理可证：，

，

，
．
．
．
是等边三角形．
，
，
当A、F、G、E共线时AE的值最大，最大值为14
故答案为：14．
作B关于AC的对称点F，D关于EC的对称点G，连接AF，FC，CG，EG，根据两点之间线段最短解决问题即可．
本题考查了全等三角形的判定及性质，轴对称的性质，等边三角形的性质，等腰直角三角形的判定与性质，勾股定理等知识；证明三角形全等是解题的关键．
 18.【答案】4：40
 【解析】【分析】
本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右顺序颠倒，且关于镜面对称．
【解答】
解：根据镜面对称的性质，题中所显示的时刻成轴对称，所以此时实际时刻为4：40．
故答案为4：40．  19.【答案】解：如图；

 ．
 【解析】见答案．
 20.【答案】解：四边形ABCD与四边形EFGH关于直线MN对称，，，
，． ，，
．
 ．
直线MN垂直平分线段BF．
 【解析】见答案．
 21.【答案】解：如图，作点A关于街道所在直线l的对称点，连结交直线l于点M，则点M即为牛奶站所在的位置．

 【解析】略
 22.【答案】解：如图所示，直线l即为所求．

如图所示，点P即为所求；
．
 【解析】解：见答案；
见答案；
的面积，
故答案为：3．
【分析】
利用网格特点，作AD的垂直平分线即可；
连接CD，与直线l的交点即为所求；
利用割补法求解可得．
本题考查了利用轴对称变换作图，三角形的面积的求解，熟练掌握网格结构准确找出对应点的位置是解题的关键．  23.【答案】解：．
由题意．
表示点到和的距离之和．
由两点之间线段最短，点在以和为端点的线段上时，代数式的值最小．
最小值．
 【解析】本题考查平面内点的坐标特点，两点间的距离公式；能够理解公式的含义，结合平面内点的坐标特点求解是关键．
利用两点间距离公式计算即可．
两点横坐标差的绝对值．
代数式表示点到和的距离之和．由两点之间线段最短，点在以和为端点的线段上时，原式值最小．