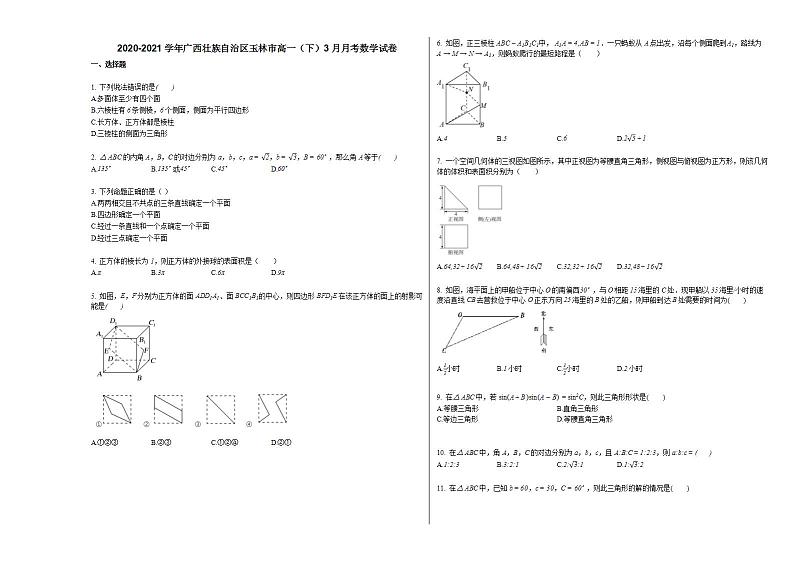
2020-2021学年广西壮族自治区玉林市高一（下）3月月考数学试卷人教A版

这是一份2020-2021学年广西壮族自治区玉林市高一（下）3月月考数学试卷人教A版，共9页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

1. 下列说法错误的是( )
A.多面体至少有四个面
B.六棱柱有6条侧棱，6个侧面，侧面为平行四边形
C.长方体、正方体都是棱柱
D.三棱柱的侧面为三角形

2. △ABC的内角A，B，C的对边分别为a，b，c，a=2，b=3，B=60∘，那么角A等于( )
A.135∘B.135∘或45∘C.45∘D.60∘

3. 下列命题正确的是（ ）
A.两两相交且不共点的三条直线确定一个平面
B.四边形确定一个平面
C.经过一条直线和一个点确定一个平面
D.经过三点确定一个平面

4. 正方体的棱长为1，则正方体的外接球的表面积是（ ）
A.πB.3πC.6πD.9π

5. 如图，E，F分别为正方体的面ADD1A1、面BCC1B1的中心，则四边形BFD1E在该正方体的面上的射影可能是( )

A.①②③B.②③C.①②④D.②①

6. 如图，正三棱柱ABC−A1B1C1中， A1A=4,AB=1．一只蚂蚁从A点出发，沿每个侧面爬到A1，路线为A→M→N→A1，则蚂蚁爬行的最短路程是（ ）

A.4B.5C.6D.25+1

7. 一个空间几何体的三视图如图所示，其中正视图为等腰直角三角形，侧视图与俯视图为正方形，则该几何体的体积和表面积分别为（ ）

A.64,32+162B.64,48+162C.32,32+162D.32,48+162

8. 如图，海平面上的甲船位于中心O的南偏西30∘，与O相距15海里的C处．现甲船以35海里/小时的速度沿直线CB去营救位于中心O正东方向25海里的B处的乙船，则甲船到达B处需要的时间为( )

A.12小时B.1小时C.32小时D.2小时

9. 在△ABC中，若sinA+BsinA−B=sin2C，则此三角形形状是( )
A.等腰三角形B.直角三角形
C.等边三角形D.等腰直角三角形

10. 在△ABC中，角A，B，C的对边分别为a，b，c，且A:B:C=1:2:3，则a:b:c= ( )
A.1:2:3B.3:2:1C.2:3:1D.1:3:2

11. 在△ABC中，已知b=60，c=30，C=60∘，则此三角形的解的情况是( )
A.有一解B.有两解
C.无解D.有解但解的个数不确定

12. 在三棱锥A−BCD中， AB⊥平面BCD， △BCD是边长为3的正三角形， AB=3，则该三棱锥的外接球的表面积为（ ）
A.21πB.6πC.24πD.15π
二、填空题

已知水平放置的四边形ABCD，按照斜二测画法画出它的直观图A′B′C′D′如图所示，其中A′D′=2，B′C′=4，A′B′=1，则DC的长度是________．


在锐角△ABC中，A，B，C所对应的边分别为a，b，c，若b=3,c=4，则a的取值范围是________．

如图，在棱长为2的正方体ABCD−A1B1C1D1中，E为DD1的中点．则三棱锥D−ACE的体积为________．


在△ABC中，角A、B、C的对边分别为a、b、c，且b+2c=2acsB，a=8, △ABC的面积为43，则b+c的值为________.
三、解答题

如图ABCD是直角梯形，以上底边CD为轴将梯形旋转一周，得到一个旋转体，求它的表面积和体积．


在△ABC中，内角A，B，C所对的边分别为a，b，c，已知3bcsC=csinB.
(1)求角C的大小；

(2)若c=27，△ABC的面积为63，求△ABC的周长．

如图，在离地面高400m的热气球上，观测到山顶C处的仰角为15∘，山脚A 处的俯角为45∘，已知∠BAC=60∘，求山的高度BC．


已知球O的半径为5.
(1)求球O的表面积；

(2)若球O有两个半径分别为3和4的平行截面，求这两个截面之间的距离．

如图，在△ABC中，B=π4，AC=25，csC=255．

(1)求sinA；

(2)记BC的中点为D，求中线AD的长．

在△ABC中，内角A，B，C所对的边分别为a，b，c，向量m→=sinB+sinC，sinA+sinB，n→=sinB−sinC,sinA，且m→⊥n→．
(1)求角C的大小；

(2)求sinA+sinB的取值范围．
参考答案与试题解析
2020-2021学年广西壮族自治区玉林市高一（下）3月月考数学试卷
一、选择题
1.
【答案】
D
【考点】
棱柱的结构特征
【解析】
此题暂无解析
【解答】
解：多面体至少为四面体即有四个面，故A正确；
根据六棱柱的性质可得其有6条侧棱，6个侧面，且侧面为平行四边形，故B正确；
长方体、正方体都是四棱柱，故C正确；
三棱柱的侧面为平行四边形，故D错误.
故选D．
2.
【答案】
C
【考点】
正弦定理
【解析】
由题设条件，可由正弦定理建立方程求出角A的三角函数值，再由三角函数值求出角，选出正确选项
【解答】
解：∵ △ABC中，角A，B，C的对边分别为
a，b，c，a=2，b=3，B=60∘，
∴ asinA=bsinB，即2sinA=3sin60∘，
∴ sinA=22，
又a=2