2020-2021学年湖南省长沙市高一（下）4月月考数学试卷人教A版

这是一份2020-2021学年湖南省长沙市高一（下）4月月考数学试卷人教A版，共10页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。


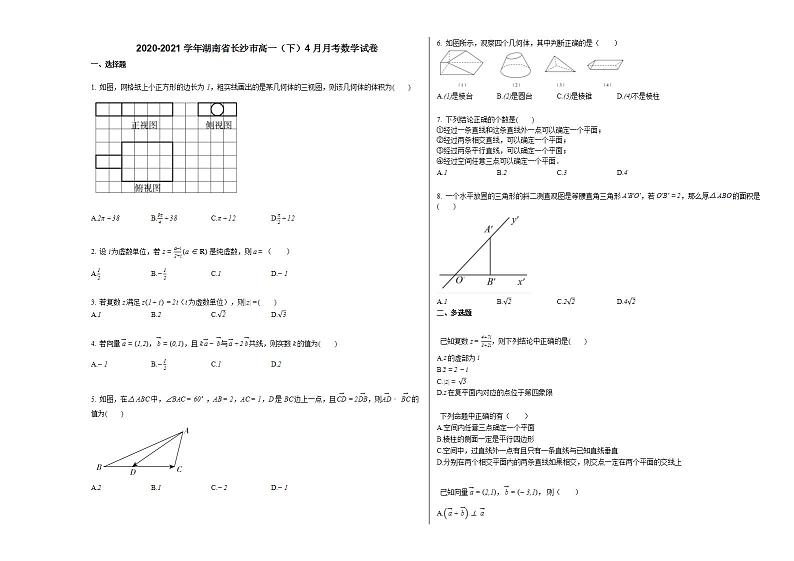
1. 如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为( )

A.2π+38B.9π4+38C.π+12D.π2+12

2. 设i为虚数单位，若 z=a−i2+ia∈R 是纯虚数，则a= （ ）
A.12 B.−12C.1D.−1

3. 若复数z满足z1+i=2i（i为虚数单位），则|z|=( )
A.1B.2C.2D.3

4. 若向量a→=1,2，b→=0,1，且ka→−b→与a→+2b→共线，则实数k的值为( )
A.−1B.−12C.1D.2

5. 如图，在△ABC中，∠BAC=60∘，AB=2，AC=1，D是BC边上一点，且CD→=2DB→，则AD→⋅BC→ 的值为( )

A.2B.1C.−2D.−1

6. 如图所示，观察四个几何体，其中判断正确的是（ ）

A.(1)是棱台B.(2)是圆台C.(3)是棱锥D.(4)不是棱柱

7. 下列结论正确的个数是( )
①经过一条直线和这条直线外一点可以确定一个平面；
②经过两条相交直线，可以确定一个平面；
③经过两条平行直线，可以确定一个平面；
④经过空间任意三点可以确定一个平面．
A.1B.2C.3D.4

8. 一个水平放置的三角形的斜二测直观图是等腰直角三角形A′B′O′，若O′B′=2，那么原△ABO的面积是( )

A.1B.2C.22D.42
二、多选题

已知复数z=4+7i3+2i，则下列结论中正确的是( )
A.z的虚部为i
B.z=2−i
C.|z|=5
D.z在复平面内对应的点位于第四象限

下列命题中正确的有（ ）
A.空间内任意三点确定一个平面
B.棱柱的侧面一定是平行四边形
C.空间中，过直线外一点有且只有一条直线与已知直线垂直
D.分别在两个相交平面内的两条直线如果相交，则交点一定在两个平面的交线上

已知向量a→=2,1，b→=−3,1， 则（ ）
A.a→+b→⊥a→
B.向量a→在向量b→上的投影向量是 −102 a→
C.|a→+2b→|=5
D.与向量a→方向相同的单位向量是255,55

已知正三棱锥P−ABC的底面边长为l，点P到底面ABC的距离为2，则( )
A.该三棱锥的内切球半径为26B.该三棱锥外接球半径为7212
C.该三棱锥体积为212D.该三棱锥体积为612
三、填空题

已知向量a→=(x+3, x2−3x−4)与MN→相等，其中M(−1,3)，N(1,3)，则x=________．

在四面体ABCD中，已知AB=AC=3，BD=BC=4，BD⊥面ABC，则四面体ABCD的外接球的半径为________．

复数z=(2m2+3i)+(m−m2i)+(−1+2mi)，m∈R，若z为纯虚数，则m等于________.

已知a、b表示两条直线，α、β、γ表示平面，给出下列条件：
①a⊂α，b⊂β，a // β，b // α；②a⊥α，b⊥β，a // b；③α⊥γ，β⊥γ；④α // γ，β // γ．
其中能推出α // β的________（把所有正确的条件序号都填上）
四、解答题

实数k为何值时，复数z=k2−3k−4+k2−5k−6i分别是
(1)实数？

(2)纯虚数？

平面内给定三个向量a→=3,2，b→=−1,2，c→=4,1，
(1)求满足a→=mb→−nc→的实数m，n；

(2)若a→+kc→//2b→−a→ ，求实数k的值．

如图，已知复平面内平行四边形ABCD中，点A对应的复数为−1， AB→对应的复数为2+2i， BC→对应的复数为4−4i．

(1)求D点对应的复数；

(2)求平行四边形ABCD的面积．

如图，在三棱柱ABC−A1B1C1中，E，F，G，H分别是AB，AC，A1B1，A1C1的中点，求证：

1B，C，H，G四点共面；

2平面EFA1 // 平面BCHG．

如图，圆锥PO的底面直径和高均是a，过PO的中点O′作平行于底面的截面，以该截面为底面挖去一个圆柱，

(1)求圆柱的表面积；

(2)求圆锥挖去圆柱剩下几何体的体积．

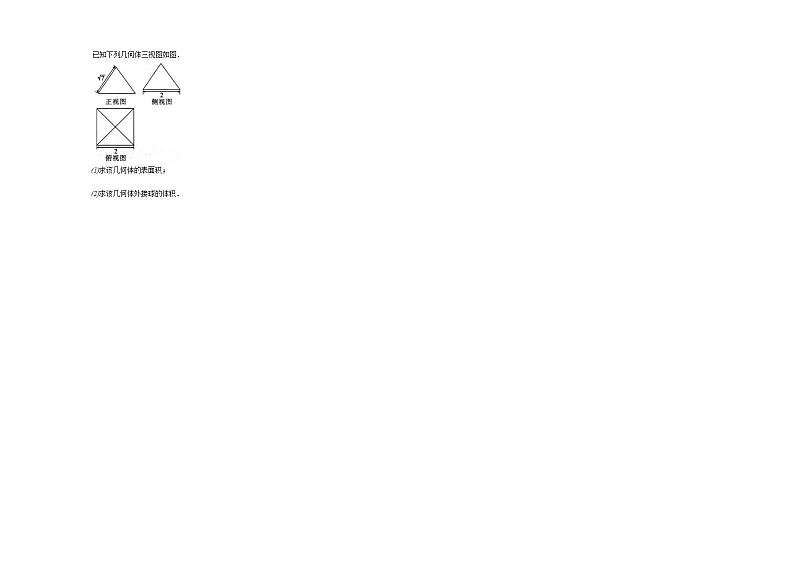
已知下列几何体三视图如图．

(1)求该几何体的表面积；

(2)求该几何体外接球的体积．
参考答案与试题解析
2020-2021学年湖南省长沙市高一（下）4月月考数学试卷
一、选择题
1.
【答案】
D
【考点】
由三视图求体积
【解析】
由三视图还原原几何体，可知该几何体为组合体，左边为圆柱，底面半径为12，高为2，右边为长方体，长、宽、高分别为
4、3、1，再由圆柱及长方体的体积公式求解．
【解答】
解：由三视图还原原几何体如图，该几何体为组合体，
左边为圆柱，底面半径为12，高为2，
右边为长方体，长、宽、高分别为4、3、1，
则该几何体的体积V=π×122×2+4×3×1=π2+12.
故选D.
2.
【答案】
A
【考点】
复数代数形式的乘除运算
复数的基本概念
【解析】
利用复数代数形式的乘除运算化简，再由实部为0且虚部不为0列式求解．
【解答】
解： z=a−i2+i=a−i2−i2+i2−i=2a−15−a+25 i是纯虚数，
∴ 2a−15=0,a+25≠0,
解得a=12.
故选A．
3.
【答案】
C
【考点】
复数的模
复数代数形式的乘除运算
【解析】
将复数进行运算化简后求模.
【解答】
解：由题意得：z=2i1+i=2i1−i1+i1−i=2i+22=1+i，
故|z|=12+12=2.
故选C．
4.
【答案】
B
【考点】
平面向量共线（平行）的坐标表示
【解析】
分别求出a→−b→与a→+2b→的坐标表示，然后再按照向量共线的条件列出方程求解即可．
【解答】
解：∵ a→=1,2，b→=0,1，
∴ ka→−b→=k,2k−1 ，a→+2b→=1,4，
又∵ ka→−b→与a→+2b→共线，
∴ 4×k−2k−1×1=0 ，
解得k=−12.
故选B．
5.
【答案】
C
【考点】
平面向量数量积的运算
【解析】
把AD→、BC→用基向量AB→、AC→表示，展开数量积得答案．
【解答】
解：∵ AD→=AC→+CD→=AC→+23CB→
=AC→+23(AB→−AC→)=23AB→+13AC→，
BC→=AC→−AB→，
∴ AD→⋅BC→=(23AB→+13AC→)⋅(AC→−AB→)
=13AC→2+13AB→⋅AC→−23AB→2
=13×12+13×2×1×cs60∘−23×22=−2．
故选C.
6.
【答案】
C
【考点】
旋转体（圆柱、圆锥、圆台）
棱锥的结构特征
棱柱的结构特征
棱台的结构特征
【解析】
利用棱锥，棱柱，棱台，圆台的定义，判断即可.
【解答】
解：棱台可以看作是圆锥，用平行底面的截面截去一个棱锥的剩余部分，所以(1)不是棱台；
(2)的几何体的上下两个底面不平行，所以(2)不是圆台；
(3)是棱锥，所以C的判断正确；
(4)是棱柱，左右两个面是棱柱的一个底面，所以D不正确.
故选C．
7.
【答案】
C
【考点】
平面的基本性质及推论
空间中直线与平面之间的位置关系
【解析】
根据公理3及其推论，确定平面的条件有不共线的三点；直线与线外一点；两条平行直线；两条相交直线，依据此判断可得答案．
【解答】
解：根据公理3及其推论，确定平面的条件有：不共线的三点，
直线与直线外一点，两条平行直线，两条相交直线，
∴ ①②③正确，④错误，
故选C．
8.
【答案】
D
【考点】
斜二测画法画直观图
【解析】
根据斜二测画法的原则确定三角形△ABO的底和高即可．
【解答】
解：因为三角形的斜二测直观图是等腰直角三角形A′B′O′，
所以△ABO的底OB=O′B′=2，腰A′O′=22，
所以△ABO是直角三角形，且高OA=2A′O′=2×22=42，
所以直角三角形△ABO的面积是12×2×42=42．
故选D．
二、多选题
【答案】
B,C
【考点】
复数代数形式的乘除运算
共轭复数
复数的代数表示法及其几何意义
【解析】
此题暂无解析
【解答】
解：∵ z=4+7i3+2i=2+i，
∴ z的虚部为1，故选项A错误；
z=2−i，故选项B正确；
|z|=22+12=5，故选项C正确；
z在复平面内对应的点位于第一象限，故选项D错误．
故选BC.
【答案】
B,D
【考点】
空间中直线与平面之间的位置关系
空间中直线与直线之间的位置关系
【解析】
利用公理及推论，棱柱的定义等逐一判断即可．
【解答】
解：对于A选项，要强调该三点不在同一直线上，故A错误；
对于B选项，由棱柱的定义可知，其侧面一定是平行四边形，故B正确；
对于C选项，若直线l⊥α，则在平面α内过异于垂足的点的任意直线都与l垂直，故C错误；
对于D选项，交点分别含于两条直线，也分别含于两个平面，必然在交线上，故D正确.
故选BD．
【答案】
A,C,D
【考点】
向量的投影
向量的数量积判断向量的共线与垂直
平面向量的坐标运算
单位向量
向量模长的计算
【解析】
可求出a→+b→⋅a→=0，从而得出选项A正确；可求出a→在b→上的投影是−12b→，从而判断选项B错误；可得出a→+2b→=−4,3，进而判断选项C正确；根据向量a→可求出与向量a→方向相同的单位向量，从而判断选项D正确．
【解答】
解：∵ a→+b→=−1,2，a→=2,1，
∴ a→+b→⋅a→=−2+2=0，a→+b→⊥a→，即A正确；
向量a→在向量b→上的投影向量是
a→⋅b→b→2⋅b→=−3×2+1×1−32+12⋅b→=−12b→，即B错误；
∵ a→+2b→=−4,3 ，
∴ |a→+2b→|=5，即C正确；
与向量a→方向相同的单位向量 a→|a→|=255,55 ，即D正确．
故选ACD.
【答案】
A,B,D
【考点】
柱体、锥体、台体的体积计算
球内接多面体
棱锥的结构特征
球的表面积和体积
【解析】
设PM是棱锥的高，则M是△ABC的中心，D是AB中点，易得几何体的体积，进而结合等体积法求得内切球的半径，利用直角三角形求解外接球的半径．
【解答】
解：如图，PM是棱锥的高，则M是△ABC的中心，D是AB中点，
S△ABC=34×12=34，VP−ABC=13S△ABC⋅PM=13×34×2=612 ，
故C错误，D正确；
DM=13×32×1=36，PD=22+362=536，CM=33，
S△PBC=12×BC×PD=12×1×536=5312，
所以S=3S△PBC+S△ABC=3×5312+34=332，
设内切球半径为r，则13Sr=VP−ABC，r=3×612332=26，故A正确；
易知外接球球心在高PM上，球心为O，设外接球半径为R，
则2−R2+332=R2 ，解得R=7212，故B正确；
故选ABD．
三、填空题
【答案】
−1
【考点】
平面向量的坐标运算
相等向量与相反向量
【解析】
利用向量的坐标运算和向量相等即可得出．
【解答】
解：因为M(−1,3)，N(1,3)，
所以MN→=(2, 0).
因为向量a→=(x+3, x2−3x−4)与向量MN→相等，
所以x+3=2,x2−3x−4=0,
解得x=−1.
故答案为：−1．
【答案】
80510
【考点】
球的表面积和体积
【解析】
利用余弦定理和正弦定理求出：△ABC的外接圆半径r，结合球心到平面ABC的距离，可得球半径．
【解答】
解：在△ABC中，∵ AB=AC=3，BC=4，
∴ csA=32+32−422×32=19，
则sinA=459，
由正弦定理得：△ABC的外接圆半径r满足：2r=asinA=4459=95，
则r=925，
又由BD⊥面ABC，BD=4，
故球心到面ABC的距离d=2，
故四面体ABCD的外接球的半径R=d2+r2=80510，
故答案为：80510.
【答案】
12
【考点】
复数的基本概念
【解析】
直接由实部为0且虚部不为0求得实数m的值
【解答】
解：由题意可得：复数z=2m2+m−1+−m2+2m+3i为纯虚数，
则2m2+m−1=0，且m2−2m−3≠0，
解得：m=12.
故答案为：12.
【答案】
②④
【考点】
平面与平面平行的判定
【解析】
根据空间中平面与平面平行的判定方法，结合空间中平面与平面平行的几何特征，逐一对题目中的四个条件进行分析，即可得到答案．
【解答】
解：若a⊂α，b⊂β，a // β，b // α，则α与β可能平行也可能相交，故①不满足条件；
若a⊥α，a // b，则b⊥α，又由b⊥β，可得α // β，故②满足条件；
若α⊥γ，β⊥γ，则α与β可能平行也可能相交，故③不满足条件；
若α // γ，β // γ，可得α // β，故④满足条件；
故答案为：②④．
四、解答题
【答案】
解：(1)z=k2−3k−4+k2−5k−6i，
当k2−5k−6=0时，z∈R，即k=6或k=−1．
(2)当k2−3k−4=0,k2−5k−6≠0时，z是纯虚数，解得k=4．
【考点】
复数的基本概念
【解析】
此题暂无解析
【解答】
解：(1)z=k2−3k−4+k2−5k−6i，
当k2−5k−6=0时，z∈R，即k=6或k=−1．
(2)当k2−3k−4=0,k2−5k−6≠0时，z是纯虚数，解得k=4．
【答案】
解：(1)∵ a→=3,2,b→=−1,2,c→=4,1，
且a→=mb→−nc→=m−1,2−n4,1=−m−4n,2m−n，
∴ −m−4n=3,2m−n=2, 解得m=59，n=−89．
(2)a→+kc→=3,2+k4,1=3+4k,2+k，
2b→−a→=2−1,2−3,2=−5,2，
∴ −52+k−23+4k=0，解得k=−1613．
【考点】
平面向量的坐标运算
平面向量共线（平行）的坐标表示
平行向量的性质
【解析】
此题暂无解析
【解答】
解：(1)∵ a→=3,2,b→=−1,2,c→=4,1，
且a→=mb→−nc→=m−1,2−n4,1=−m−4n,2m−n，
∴ −m−4n=3,2m−n=2, 解得m=59，n=−89．
(2)a→+kc→=3,2+k4,1=3+4k,2+k，
2b→−a→=2−1,2−3,2=−5,2，
∴ −52+k−23+4k=0，解得k=−1613．
【答案】
解：(1)依题意，点A对应的复数为−1，AB→对应的复数为2+2i，
可得A−1,0，AB→=2,2，可得B1,2．
又BC→对应的复数为4−4i，得BC→=4,−4，可得C(5,−2）．
设D点对应的复数为x+yi，x,y∈R.
得CD→=(x−5,y+2)，BA→=(−2,−2)，
∵ 四边形ABCD为平行四边形，
∴ BA→=CD→ ，
解得x=3， y=−4，
故D点对应的复数为3−4i．
(2)AB→=2,2，BC→=4,−4，
可得： AB→⋅BC→=0，∴ AB⊥BC，
|AB→|=22， |BC→|=42，
故平行四边形ABCD的面积为22×42=16．
【考点】
复数的代数表示法及其几何意义
平面向量坐标表示的应用
向量的模
【解析】
此题暂无解析
【解答】
解：(1)依题意，点A对应的复数为−1，AB→对应的复数为2+2i，
可得A−1,0，AB→=2,2，可得B1,2．
又BC→对应的复数为4−4i，得BC→=4,−4，可得C(5,−2）．
设D点对应的复数为x+yi，x,y∈R.
得CD→=(x−5,y+2)，BA→=(−2,−2)，
∵ 四边形ABCD为平行四边形，
∴ BA→=CD→ ，
解得x=3， y=−4，
故D点对应的复数为3−4i．
(2)AB→=2,2，BC→=4,−4，
可得： AB→⋅BC→=0，∴ AB⊥BC，
|AB→|=22， |BC→|=42，
故平行四边形ABCD的面积为22×42=16．
【答案】
证明：1∵ G，H分别为A1B1，A1C1中点，
∴ GH // B1C1，
∵ 三棱柱ABC−A1B1C1中，BC // B1C1，
∴ GH // BC，
∴ B，C，H，G四点共面；
2∵ E，F分别为AB，AC中点，
∴ EF // BC，
又∵ E，G分别为三棱柱侧面
平行四边形AA1B1B对边AB，A1B1中点，
∴ 四边形A1EBG为平行四边形，A1E // BG，
∵ A1E∩EF=E，BG∩BC=B，
A1E⊂ 平面EFA1，EF⊂平面EFA1，
BG⊂平面BCHG，BC⊂平面BCHG，
∴ 平面EFA1 // 平面BCHG．
【考点】
平面的基本性质及推论
平面与平面平行的判定
【解析】
（1）利用三角形中位线的性质，证明GH // B1C1，从而可得GH // BC，即可证明B，C，H，G四点共面；
（2）证明平面EFA1中有两条直线A1E、EF分别与平面BCHG中的两条直线BG、BC平行，即可得到平面EFA1 // 平面BCHG．
【解答】
证明：1∵ G，H分别为A1B1，A1C1中点，
∴ GH // B1C1，
∵ 三棱柱ABC−A1B1C1中，BC // B1C1，
∴ GH // BC，
∴ B，C，H，G四点共面；
2∵ E，F分别为AB，AC中点，
∴ EF // BC，
又∵ E，G分别为三棱柱侧面
平行四边形AA1B1B对边AB，A1B1中点，
∴ 四边形A1EBG为平行四边形，A1E // BG，
∵ A1E∩EF=E，BG∩BC=B，
A1E⊂ 平面EFA1，EF⊂平面EFA1，
BG⊂平面BCHG，BC⊂平面BCHG，
∴ 平面EFA1 // 平面BCHG．
【答案】
解：(1)设圆锥底面半径为r，圆柱底面半径为r′，
因为过PO的中点O​′作平行于底面的截面，以该截面为底面挖去一个圆柱，
可得r=a2，r​′=a4 ，且圆柱母线长l′=a2，圆锥母线长l=a2+a22=52a，
所以圆柱的表面积为：S表=2πr′2+2πr′l′
=2π⋅a42+2π⋅a4⋅a2=38πa2.
(2)剩下几何体的体积V=13πr2⋅OP−πr2⋅OO′
=13π⋅a22⋅a−πa42⋅a2=596πa2.
【考点】
柱体、锥体、台体的侧面积和表面积
柱体、锥体、台体的体积计算
组合几何体的面积、体积问题
【解析】
无
无
【解答】
解：(1)设圆锥底面半径为r，圆柱底面半径为r′，
因为过PO的中点O​′作平行于底面的截面，以该截面为底面挖去一个圆柱，
可得r=a2，r​′=a4 ，且圆柱母线长l′=a2，圆锥母线长l=a2+a22=52a，
所以圆柱的表面积为：S表=2πr′2+2πr′l′
=2π⋅a42+2π⋅a4⋅a2=38πa2.
(2)剩下几何体的体积V=13πr2⋅OP−πr2⋅OO′
=13π⋅a22⋅a−πa42⋅a2=596πa2.
【答案】
解：(1)由三视图知，该几何体是正四棱锥的直观图，
底面为正方形，边长为2，
其面积为2×2=4，
四个侧面是全等的三角形，斜高为7，其面积为4×12×2×7=47，
∴ 该几何体的表面积为47+4．
(2)根据斜高为7，底面边长为2，
可得高SO=7−1=6，OA=2，
设正四棱锥的外接球的球心为O′，
由对称性知O′在SO上，
设OO′=ℎ, 球的半径为r，∴ ℎ=6−r，
r=ℎ2+OA2=8−26r+r2,
解得r=263，
则球的体积V=43πr3=646π27.
【考点】
由三视图求表面积
棱柱、棱锥、棱台的侧面积和表面积
球内接多面体
球的表面积和体积
【解析】
（1）首先根据几何体的三视图，转换为几何体的直观图，进一步求出几何体的表面积；
（2）利用几何体和球体的关系，进一步求出球体的半径，最后求出球体的体积．
【解答】
解：(1)由三视图知，该几何体是正四棱锥的直观图，
底面为正方形，边长为2，
其面积为2×2=4，
四个侧面是全等的三角形，斜高为7，其面积为4×12×2×7=47，
∴ 该几何体的表面积为47+4．
(2)根据斜高为7，底面边长为2，
可得高SO=7−1=6，OA=2，
设正四棱锥的外接球的球心为O′，
由对称性知O′在SO上，
设OO′=ℎ, 球的半径为r，∴ ℎ=6−r，
r=ℎ2+OA2=8−26r+r2,
解得r=263，
则球的体积V=43πr3=646π27.