2020-2021学年山东省枣庄市新校高一（下）5月周测数学试卷人教A版

这是一份2020-2021学年山东省枣庄市新校高一（下）5月周测数学试卷人教A版，共13页。试卷主要包含了选择题，多选题，填空题，解答题等内容，欢迎下载使用。

1. 已知复数z=5−5i2−i，则z的虚部为( )
A.−3B.−3iC.−1D.−i

2. 已知向量a→=(3,2)，b→=(k,3)，c→=(−1,2)，且2a→−b→⊥c→，则实数k等于( )
A.112B.132C.8D.4

3. 阿基米德是古希腊伟大的数学家、物理学家、天文学家，是静态力学和流体静力学的奠基人，和高斯、牛顿并列为世界三大数学家，他在不知道球体积公式的情况下得出了圆柱容球定理，即圆柱内切球(与圆柱的两底面及侧面都相切的球)的体积等于圆柱体积的三分之二．那么，圆柱内切球的表面积与该圆柱表面积的比为( )
A.12B.13C.23D.34

4. 已知m，n是不同的直线，α，β是不重合的平面，则下列说法正确的是( )
A.若m//α，则m平行于平面α内的任意一条直线
B.若m//α ，n//α，则m//n
C.若α//β，m⊂α，n⊂β，则m//n
D.若α//β，m⊂α，则m//β

5. 在△ABC中， sinA:sinB:sinC=1:5:21，则△ABC最大角和最小角之和为( )
A.90∘B.120∘C.135∘D.150∘

6. 如图ABCD−A1B1C1D1是长方体，O是B1D1的中点，直线A1C交平面AB1D1于点M，则下列结论错误的是（ ）

A.A，M，O三点共线B.M，O，A1，A四点共面
C.B，B1，O，M四点共面D.A，O，C，M四点共面

7. 在△ABC中，内角A，B，C的对边分别为a，b，c，若△ABC的面积为S，且a=1，4S=b2+c2−a2，则△ABC外接圆的半径为（ ）
A.2B.2C.1D.22

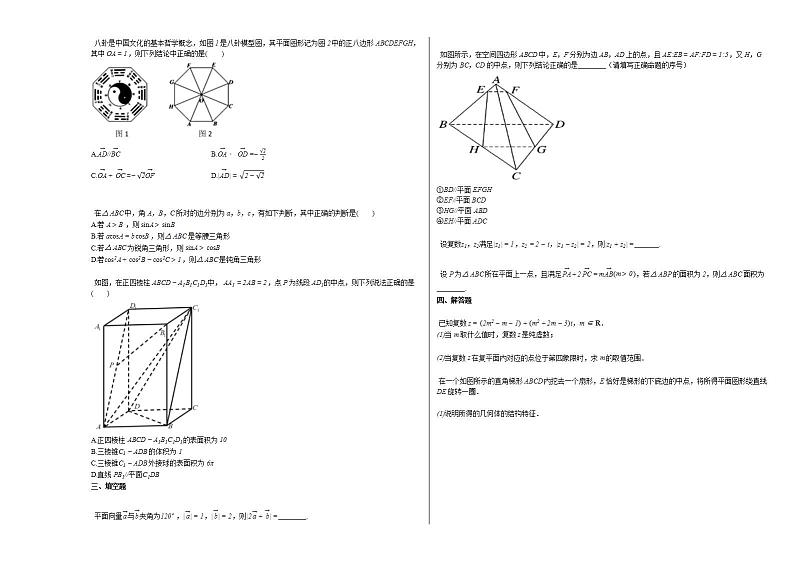
8. 如图，O是△ABC的重心，AB→=a→，AC→=b→，D是边BC上一点，且BD→=4DC→，则( )

A.OD→=−215a→+715b→B.OD→=215a→−715b→
C.OD→=−215a→−715b→D.OD→=215a→+715b→
二、多选题

已知i为虚数单位，则下列结论正确的是( )
A.若复数z1，z2互为共轭复数，则z1⋅z2为实数
B.若复数z1，z2满足|z1|=|z2|，则z1，z2互为共轭复数
C.若复数z满足1z∈R，则z∈R
D.对任意的复数z，都有z2≥0

八卦是中国文化的基本哲学概念，如图1是八卦模型图，其平面图形记为图2中的正八边形ABCDEFGH，其中OA=1，则下列结论中正确的是( )

A.AD→//BC→B.OA→⋅OD→=−22
C.OA→+OC→=−2OF→D.|AD→|=2−2

在△ABC中，角A，B，C所对的边分别为a，b，c，有如下判断，其中正确的判断是( )
A.若A>B ，则sinA>sinB
B.若acsA=bcsB ，则△ABC是等腰三角形
C.若△ABC为锐角三角形，则sinA>csB
D.若cs2A+cs2B−cs2C>1，则△ABC是钝角三角形

如图，在正四棱柱ABCD−A1B1C1D1中， AA1=2AB=2，点P为线段AD1的中点，则下列说法正确的是( )

A.正四棱柱ABCD−A1B1C1D1的表面积为10
B.三棱锥C1−ADB的体积为1
C.三棱锥C1−ADB外接球的表面积为6π
D.直线PB1//平面C1DB
三、填空题

平面向量a→与b→夹角为120∘，|a→|=1，|b→|=2，则|2a→+b→|=________.

如图所示，在空间四边形ABCD中，E，F分别为边AB，AD上的点，且AE:EB=AF:FD=1:5，又H，G分别为BC，CD的中点，则下列结论正确的是________（请填写正确命题的序号）
①BD//平面EFGH
②EF//平面BCD
③HG//平面ABD
④EH//平面ADC

设复数z1，z2满足|z1|=1，z2=2−i，|z1−z2|=2，则|z1+z2|=_______.

设P为△ABC所在平面上一点，且满足PA→+2PC→=mAB→m>0，若△ABP的面积为2，则△ABC面积为________.
四、解答题

已知复数z=2m2−m−1+m2+2m−3i，m∈R．
(1)当m取什么值时，复数z是纯虚数；

(2)当复数z在复平面内对应的点位于第四象限时，求m的取值范围．

在一个如图所示的直角梯形ABCD内挖去一个扇形，E恰好是梯形的下底边的中点，将所得平面图形绕直线DE旋转一圈．

(1)说明所得的几何体的结构特征．

(2)求所得几何体的表面积和体积．

已知|a→|=1，|b→|=3，a→+b→2=1．
(1)求a→与b→的夹角θ；

(2)在平面四边形ABCD中，若BA→=a→，BC→=b→， AD=213， ∠ADC=2∠ACD，求△ACD的面积．

在①3b−3ccsA=asinC，②ab=12tanCtanB+1，③sinA−sinCb=sinA−sinBa+c这三个条件中任选一个，补充在下面的问题中，并解答问题．
在△ABC中，内角A，B，C的对边分别为a，b，c，且满足________．
(1)求C．

(2)若△ABC的面积为3，D在边AC上，且CD=13CA，求BD的最小值．
注：如果选择多个条件分别解答，按第一个解答计分．

如图，四棱锥P−ABCD中， PD⊥平面ABCD，AB//CD， CD=2AB=2， AB⊥AD，PD=1，F在线段CD上，DC=4DF， BF=52．
(1)求三棱锥D−PBC的体积；

(2)线段PA上是否存在一点E，使DE//平面PBF？若存在，请确定点E的位置；若不存在，请说明理由；

(3)若M为AB的中点，在(2)的条件下，过ME的平面交平面PBD于直线l ，求证： ME//l．

如图所示，某市有一块空地△OAB，其中OA=2km，∠OAM=60，∠AOB=90∘．当地政府计划将这块空地改造成一个旅游景点，拟在中间挖一个人工湖△OMN，其中M，N都在边AB上，且∠MON=30∘，挖出的泥土堆放在△OAM地带上形成假山，剩下的△OBN地带开设儿童游乐场．为安全起见，需在△OAN的周围安装防护网．设∠AOM=θ．

(1)当AM=1km时，求此时防护网的总长度；

(2)若θ=15，问此时人工湖用地△OMN的面积是堆假山用地△OAM的面积的多少倍？

(3)为节省投入资金，人工湖△OMN的面积要尽可能小，问如何设计施工方案，可使△OMN的面积最小？最小面积是多少？
参考答案与试题解析
2020-2021学年山东省枣庄市新校高一（下）5月周测数学试卷
一、选择题
1.
【答案】
C
【考点】
复数代数形式的乘除运算
复数的基本概念
【解析】
由题意，先对复数z进行整理，进而即可得到复数的虚部.
【解答】
解：已知复数z=5−5i2−i=5(1−i)(2+i)(2+i)(2−i)
=5(3−i)5=3−i ，
可得z的虚部为−1.
故选C.
2.
【答案】
D
【考点】
平面向量的坐标运算
数量积判断两个平面向量的垂直关系
【解析】
由题意，根据所给向量得到2a→−b→=(6−k,1)，若两向量垂直，其数量积为零，代入求解即可.
【解答】
解：已知a→=(3,2)，b→=(k,3)，c→=(−1,2)，
所以2a→−b→=(6−k,1)，
若(2a→−b→)⊥c→，
即−(6−k)+2×1=0，
解得k=4.
故选D.
3.
【答案】
C
【考点】
球的表面积和体积
圆柱表面积的有关计算
【解析】
由圆柱内切球特点：圆柱内切球与圆柱的两底面及侧面都相切，知：圆柱内切球的半径等于底面(圆柱底面)半径，圆柱内切球的直径等于圆柱体的高，据此根据球和圆柱的表面积及体积公式列式求解．
【解答】
解：由圆柱内切球特点：圆柱内切球与圆柱的两底面及侧面都相切，知：圆柱内切球的半径等于底面(圆柱底面)半径，圆柱内切球的直径等于圆柱体的高，
设圆柱底面半径为r，则高为 ℎ=2r，球的半径为r，
则V圆柱=Sℎ=πr2⋅2r，则V圆柱=2πr3，
由容球定理有： V球=23V圆柱=43πr3，
内切球面积S球=4πr2，
圆柱表面积 S圆柱=2×πr2+2πr×ℎ=2πr2+4πr2=6πr2，
综上所述 S球S圆柱=4πr26πr2=23．
故选C．
4.
【答案】
D
【考点】
空间中直线与平面之间的位置关系
空间中直线与直线之间的位置关系
【解析】
由题意，根据空间中直线与平面位置关系和直线与直线位置关系的判断对选项进行逐一分析，进而即可求解.
【解答】
解：对于选项A，若m//α，则直线m与平面α内的直线没有公共点，即直线m平行于平面α内的直线或互为异面，故选项A错误；
对于选项B，若m//α ，n//α，则m与n平行，相交或是异面，故选项B错误；
对于选项C，若α//β，m⊂α，n⊂β，此时m//n或直线m与直线n异面，故选项C错误；
对于选项D，若α//β，m⊂α，则m//β，故选项D正确.
故选D.
5.
【答案】
B
【考点】
正弦定理
余弦定理
【解析】
由题意，根据三角形中大边对大角可得角A的角最小，角B的角最大，利用正弦定理得a:b:c=1:5:21，设a=x，利用余弦定理以及三角形内角和求出C=60​∘，进而可得则△ABC最大角和最小角之和.
【解答】
解：已知在△ABC中， sinA:sinB:sinC=1:5:21，
所以角A的角最小，角B的角最大，
由正弦定理得a:b:c=1:5:21，
不妨设a=x，则b=5x，c=21x，
由余弦定理得csC=a2+b2−c22ab=x2+25x2−21x210x2=12，
因为0sinB，故A选项正确；
对于B选项， acsA=bcsB，由正弦定理化简得sin2A=sin2B，
所以A=B或A+B=π2 ，
则△ABC是等腰三角形或直角三角形，故B选项错误；
对于C选项，因为△ABC是锐角三角形，
所以A+B>π2，即sinA>sinπ2−B=csB，故C选项正确；
对于D选项，因为cs2A+cs2B−cs2C>1，
所以1−sin2A+1−sin2B−1+sin2C>1，
所以c2>a2+b2，
∴ a2+b2−c22ab