初中数学湘教版九年级上册第3章 图形的相似3.2 平行线分线段成比例精品课时练习

这是一份初中数学湘教版九年级上册第3章 图形的相似3.2 平行线分线段成比例精品课时练习，共16页。
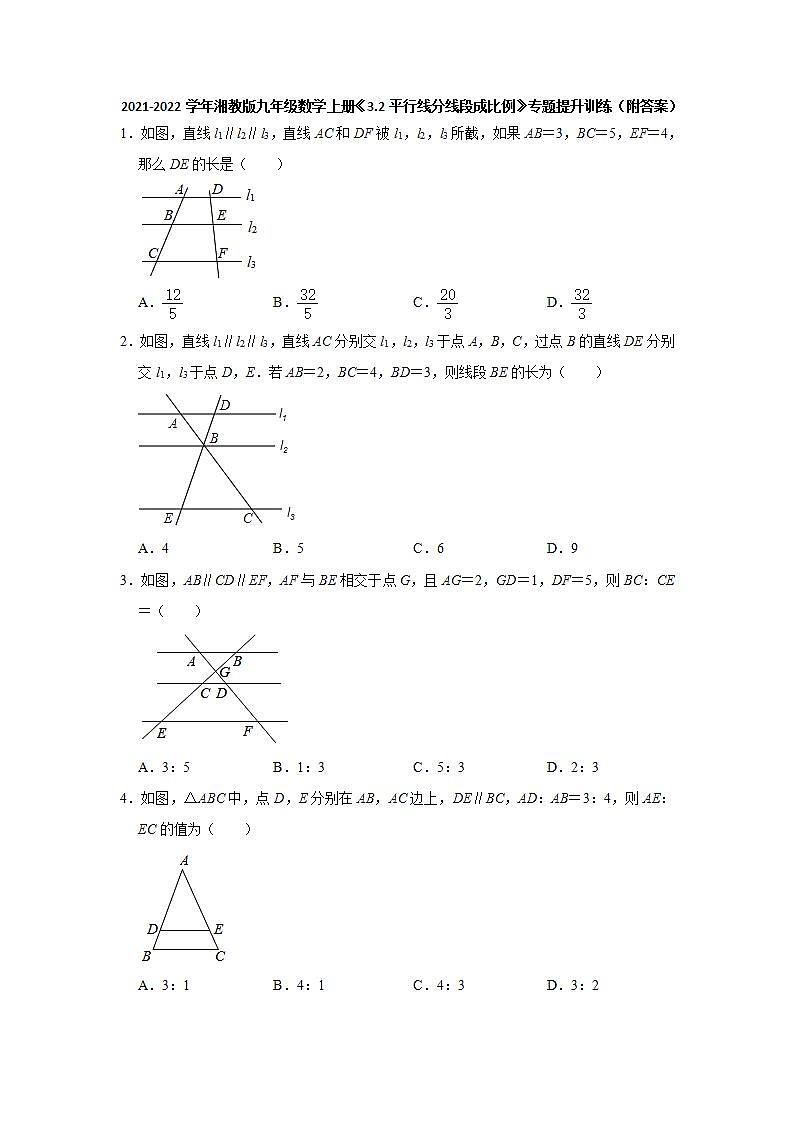
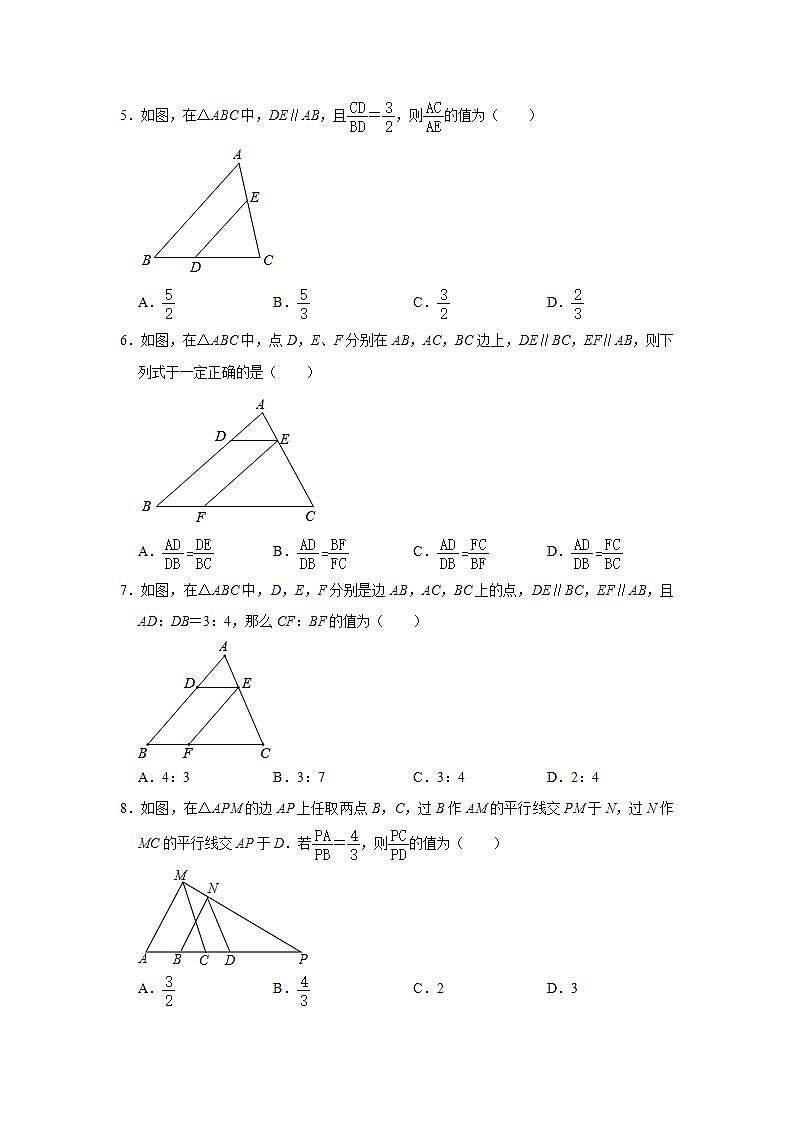
2021-2022学年湘教版九年级数学上册《3.2平行线分线段成比例》专题提升训练（附答案）1．如图，直线l1∥l2∥l3，直线AC和DF被l1，l2，l3所截，如果AB＝3，BC＝5，EF＝4，那么DE的长是（　　）A． B． C． D．2．如图，直线l1∥l2∥l3，直线AC分别交l1，l2，l3于点A，B，C，过点B的直线DE分别交l1，l3于点D，E．若AB＝2，BC＝4，BD＝3，则线段BE的长为（　　）A．4 B．5 C．6 D．93．如图，AB∥CD∥EF，AF与BE相交于点G，且AG＝2，GD＝1，DF＝5，则BC：CE＝（　　）A．3：5 B．1：3 C．5：3 D．2：34．如图，△ABC中，点D，E分别在AB，AC边上，DE∥BC，AD：AB＝3：4，则AE：EC的值为（　　）A．3：1 B．4：1 C．4：3 D．3：25．如图，在△ABC中，DE∥AB，且＝，则的值为（　　）A． B． C． D．6．如图，在△ABC中，点D，E、F分别在AB，AC，BC边上，DE∥BC，EF∥AB，则下列式于一定正确的是（　　）A． B． C． D．7．如图，在△ABC中，D，E，F分别是边AB，AC，BC上的点，DE∥BC，EF∥AB，且AD：DB＝3：4，那么CF：BF的值为（　　）A．4：3 B．3：7 C．3：4 D．2：48．如图，在△APM的边AP上任取两点B，C，过B作AM的平行线交PM于N，过N作MC的平行线交AP于D．若＝，则的值为（　　）A． B． C．2 D．39．如图，AB，CD相交于点E，且AC∥EF∥DB，点C，F，B在同一条直线上．已知AC＝p，EF＝r，DB＝q，则p，q，r之间满足的数量关系式是（　　）A．+＝ B．+＝ C．+＝ D．+＝10．如图，在平行四边形ABCD中，点F是AD上的点，AF＝2FD，直线BF交AC于点E，交CD的延长线于点G，则的值为（　　）A． B． C． D．11．如图，AB与CD相交于点E，点F在线段BC上，且AC∥EF∥DB．若BE＝5，BF＝3，AE＝BC，则的值为（　　）A． B． C． D．12．如图，已知AM：MD＝4：1，BD：DC＝2：3，则AE：EC＝（　　）A．4：3 B．8：5 C．6：5 D．3：213．在△ABC中，点E在AC上，且，F为BE中点，AF的延长线交BC于D，则：＝（　　）A．1：2 B．1：3 C．1：4 D．2：314．如图，在△ABC中，D是BC上一点，连接AD，，F是AD的中点，连接BF并延长交AC于E，则的值是（　　）A． B． C． D．15．如图，已知：l1∥l2∥l3，AB＝2，BC＝4，DF＝12．求DE的长．16．如图，在△ABC中，点D，E分别在AB，AC的边上，DE∥BC，AD＝6，DB＝3，AE＝4，求AC的长． 17．如图，D是△ABC的边AB的中点，DE∥BC，CE∥AB，AC与DE相交于F，求证：F是DE的中点．18．如图，DE∥AB，EF∥BC，AF＝5cm，FB＝3cm，CD＝2cm，求BD的长．19．如图，AD与BC相交于点E，点F在BD上，且AB∥EF∥CD，若EF＝2，CD＝3，则AB的长为多少？20．如图，在△ABC中，D是AB 上一点，且＝，E、F是AC上的点，且DE∥BC，DF∥BE，AF＝9．求EC的长．21．如图，在△ABC中，DE∥BC，在BC上取一点M，使＝，连接AM交DE于N．求证：NE＝2DN．22．如图，DE∥BC，EF∥CG，AD：AB＝1：3，AE＝3．（1）求EC的值；（2）求证：AD•AG＝AF•AB．23．已知：平行四边形ABCD，E是BA延长线上一点，CE与AD、BD交于G、F．求证：CF2＝GF•EF．24．如图，在△ABC中，AD与BE相交于点G，且＝4，＝．（1）求的值；（2）若CE＝5cm，则AC的长．25．如图，△ABC中，D是AC的中点，E在AB上，BD、CE交于O点．已知：OB：OD＝1：2，求值． 26．如图，在Rt△ABC中，∠C＝90°，AC＝4cm，BC＝5cm，点D在BC上，且CD＝3cm，现有两个动点P，Q分别从点A和点B同时出发，其中点P以1厘米/秒的速度沿AC向终点C运动；点Q以1.25厘米/秒的速度沿BC向终点C运动，过点P作PE∥BC交AD于点E，连接EQ，设动点运动时间为t秒（t＞0）．（1）CP＝　        　，CQ＝　        　．（用含t的代数式表示）（2）连接PQ，在运动过程中，不论t取何值时，总有线段PQ与线段AB平行，为什么？
参考答案1．解：∵直线l1∥l2∥l3，∴，∵AB＝3，BC＝5，EF＝4，∴，∴DE＝．故选：A．2．解：∵l1∥l2∥l3，AB＝2，BC＝4，BD＝3，∴，∴，解得：BE＝6，故选：C．3．解：∵AB∥CD∥EF，∴＝＝＝．故选：A．4．解：∵AD：AB＝3：4，∴AD：DB＝3：1，∵DE∥BC，∴AE：EC＝AD：DB＝3：1，故选：A．5．解：∵DE∥AB，∴＝＝，∴＝．故选：A．6．解：∵DE∥BC，∴，∵EF∥AB，∴，∴，故选：B．7．解：∵DE∥BC，EF∥AB，AD：DB＝3：4，∴，∴，故选：A．8．解：∵BN∥AM，＝，∴＝，∵DN∥CM，∴＝＝，故选：B．9．解：∵AC∥EF，∴，∵EF∥DB，∴，∴＝+＝＝＝1，即＝1，∴．故选：C．10．解：由AF＝2DF，可以假设DF＝k，则AF＝2k，AD＝3k，∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，AD＝BC＝3k，∴＝＝，∴＝＝故选：C．11．解：设CF＝x，∵EF∥AC，∴＝，∴＝，解得x＝，∴CF＝，∵EF∥DB，∴＝＝＝．故选：A．12．解：过点D作DF∥BE交AC于F，则＝＝4，＝＝，∴AE：EC＝8：5，故选：B．13．解：过E点作EH∥BC交AD于H，如图，∵F为BE中点，∴EF＝BF，∵HE∥BD，∴＝＝1，即BD＝EH，∵HE∥CD，∴＝，∵＝，∴＝＝，∴＝，即CD＝3HE，∴＝＝．故选：B．14．解：过D点作DH∥BE交AC于H，如图，∵F点为AD的中点，∴AF＝FD，∵FE∥DH，∴＝＝1，即AE＝EH，∵DH∥BE，∴＝＝，CH＝3EH，∴＝．故选：A．15．解：∵l1∥l2∥l3，AB＝2，BC＝4，DF＝12，∴＝，即＝，解得DE＝4．16．解：∵DE∥BC，∴．∵AD＝6，DB＝3，AE＝4，∴．∴EC＝2．∴AC＝AE+EC＝6．17．证明：∵D是△ABC的边AB的中点，∴AD＝DB，∵DE∥BC，∴＝＝1，∴AF＝FC，∵CE∥AB，∴＝＝1，∴DF＝EF，即F是DE的中点．18．解：∵DE∥AB，EF∥BC，AF＝5cm，FB＝3cm，CD＝2cm，∴，∴＝，∴，解得：BD＝cm．19．解：∵EF∥CD，∴＝，∵EF＝2，CD＝3，∴＝，∵AB∥EF，∴＝＝，∴AB＝6．故答案为：6．20．解：∵DF∥BE，∴∵，AF＝9，∴FE＝6．∵DE∥BC，∴＝∵AE＝AF+FE＝15，∴EC＝1021．证明：∵DE∥BC，∴＝，＝，∴＝，∴＝＝，∴NE＝2DN．22．（1）解：∵DE∥BC，∴＝，又＝，AE＝3，∴＝，解得AC＝9，∴EC＝AC﹣AE＝9﹣3＝6；（2）证明：∵DE∥BC，EF∥CG，∴＝＝，∴AD•AG＝AF•AB．23．证明：∵四边形ABCD是平行四边形，∴AD∥BC，AB∥CD，∴＝，＝，∴＝，即CF2＝GF•EF．24．解：（1）过点D作DF∥BE交AC于点F，∴＝＝4，∴AE＝4EF，∵DF∥BE，∴＝＝，∴CE＝EF，∴＝＝；（2）∵＝，∴＝，解得，AE＝8，∴AC＝AE+CE＝8+5＝13（cm）．25．解：取AE中点F，连DF，如图，∵D是AC中点，F为AE的中点，∴DF为△AEC的中位线，∴DF∥CE，∵OE∥DF，∴＝＝，∴＝．26．解：（1）∵AC＝4cm，BC＝5cm，∴CP＝AC﹣AP＝（4﹣t）cm，CQ＝（5﹣1.25t）cm，故答案为：（4﹣t）cm，（5﹣1.25t）cm；（2）如图，∵点P以1厘米/秒的速度从点A沿AC向终点C运动，点Q以1.25厘米/秒的速度从点B沿BC向终点C运动，∴AP＝t，BQ＝1.25t，∴PC＝AC﹣AP＝4﹣t，QC＝BC﹣BQ＝5﹣1.25t，∴＝＝1﹣，＝＝1﹣，∴＝，∴PQ∥AB．