初中人教版24.3 正多边形和圆第1课时教学设计

教学

环节

教师活动

学生活动

设计意图

环节一

创设情境

【学习目标】

1.了解正多边形和圆的关系，了解正多边形的半径、边长、中心、中心角、边心距等概念；

2.结合生活中的正多边形形状的图案，发现正多边形和圆的关系，学会用圆的有关知识解决正多边形的问题；

3.在探索正多边形和圆的关系的过程中，感受特殊到一般的学习方法，发展学生的逻辑思维能力和推理能力；

4.学生经历观察、发现、探究等数学活动，感受数学来源于生活，又服务于生活，体会事物之间是相互联系、相互作用的.

熟悉学习目标

通过学习目标让学生熟悉本节课要讲解的内容，教学目标从知识技能、数学思考、解决问题、情感态度等方面着眼设计.

问题：观看下面的视频，试着想一想，日常生活中，还有哪些正多边形形状的物体，或利用正多边形组成的美丽图案?

认真观看视频并思考

通过视频引入提高学生的学习兴趣，同时引导学生回顾正多边形的概念，发现生活中由正多边形组成的图案，为学习正多边形和圆的关系作铺垫.

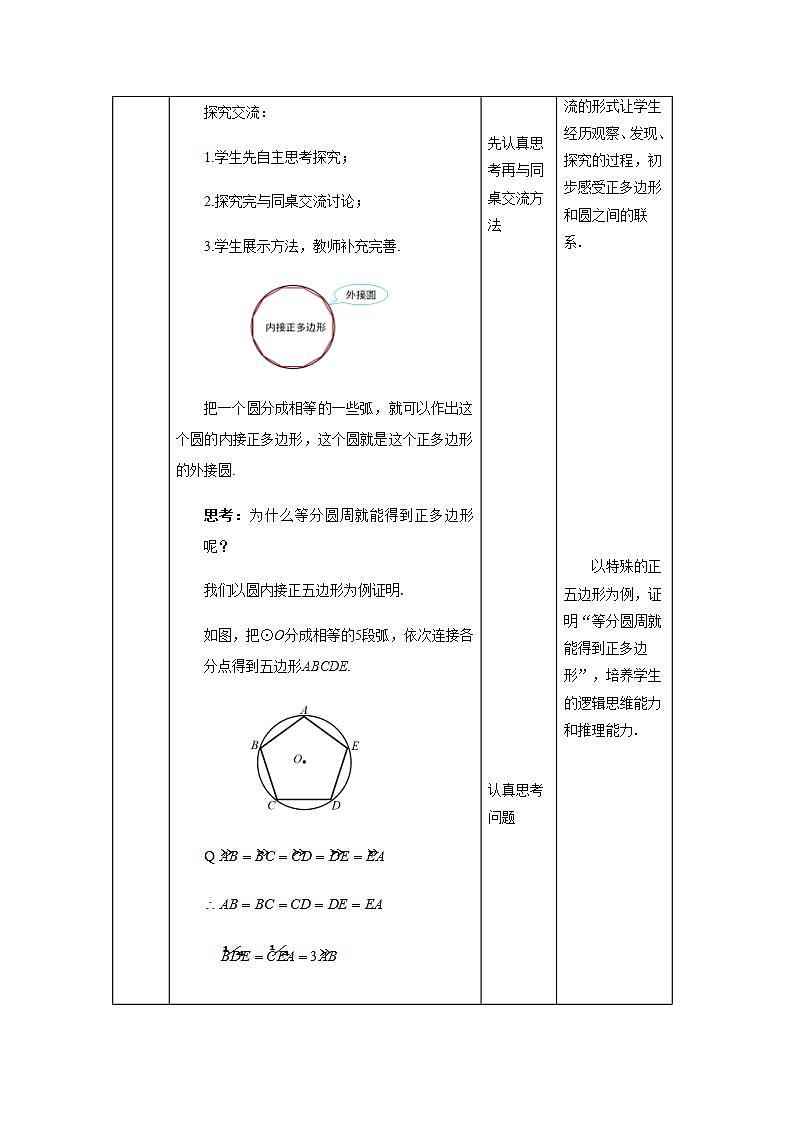
环节二 探究新知

问题：正多边形的边数无限增多，就接近于圆，那么给你一个圆，如何能在圆内作出一个正多边形呢？

探究交流：

1.学生先自主思考探究；

2.探究完与同桌交流讨论；

3.学生展示方法，教师补充完善.

把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆.

思考：为什么等分圆周就能得到正多边形呢？

我们以圆内接正五边形为例证明.

如图，把⊙O分成相等的5段弧，依次连接各分点得到五边形ABCDE.

同理

又  五边形ABCDE的顶点都在⊙O上，

∴五边形ABCDE是⊙O的内接正五边形，

⊙O是正五边形ABCDE的外接圆.

思考：根据刚才的证明过程你能整理出一般的证明思路吗？

同圆中，由弧相等可得弦相等，而弦相等就相当于多边形的各边都相等，同理，由弧相等可得圆周角相等，而圆周角相等就相当于多边形的各角都相等.又因为各边相等各角也相等的多边形是正多边形，所以等分弧就可以得到正多边形.

把圆分成n（n≥3）等份：依次连接各分点所得的多边形一定是   正n边形      ，这个正n边形是这个圆的   内接正n边形  ，这个圆是这个正n边形的   外接圆   .

思考：圆中的元素和正多边形有什么关系呢？

正多边形的外接圆的圆心叫做这个

正多边形的中心.

外接圆的半径叫做正多边形的半径.

正多边形的每一边所对的圆心角叫

做正多边形的中心角.

中心到正多边形的一边的距离叫做

正多边形的边心距.

完成下面的表格.

正多边形的外角=中心角

先认真思考再与同桌交流方法

认真思考问题

熟悉证明过程和证明依据

整理刚才的证明思路

归纳并完成填空

熟悉相关概念

认真完成表格

通过自主交流的形式让学生经历观察、发现、探究的过程，初步感受正多边形和圆之间的联系.

以特殊的正五边形为例，证明“等分圆周就能得到正多边形”，培养学生的逻辑思维能力和推理能力.

通过整理证明思路让学生进一步熟悉正多边习形和圆的关系，感受“特殊—一般”的学习方法.

以填空的形式让学生进一步熟悉如何由一个圆作正多边形，同时熟悉外接圆的概念，培养学生的归纳整理能力.

结合图形，加深学生对中心、半径、中心角、边心距的理解.

通过抢答的形式让学生进一步熟悉正多边形和圆的相关概念，提高学生的学习积极性，并为后面的解题作准备.

环节三

应用新知

【例】如图，有一个亭子，它的地基是半径为4 m的正六边形，求地基的周长和面积.（结果保留小数点后一位）.

    提示：关键是求出正多边形的边长和边心距，作辅助线利用勾股定理求解.

解：如图，连接OB，OC.因为六边形ABCDEF是正六边形，所以它的中心角等于，△OBC是等边三角形，从而正六边形的边长等于它的半径．

因此，亭子地基的周长l =4×6=24(m)．

作OP⊥BC，垂足为P，在Rt△OPC中，

OC =4， PC =，

    利用勾股定理，可得边心距

亭子地基的面积

圆内接正多边形常用辅助线

①       连半径，得中心角

②       作边心距，得直角三角形

由勾股定理得

明确本题的做法

熟悉正多边形中常用辅助线

   让学生在应用过程中进一步加深对正多边形和圆的认识和理解，培养学生的应用意识和推理能力.同时在解题过程中渗透转化思想，将正多边形的面积转化成几个三角形的面积之和.

通过例题归纳出圆内接正多边形中常用的辅助线，培养学生的归纳总结能力.

环节四

巩固新知

1．下列命题正确的是(　  　)

　　A．各边相等的多边形是正多边形        

　　B．各角相等的多边形是正多边形

　　C．既是轴对称图形又是中心对称图形的多边形是正多边形

　　D．各边相等，各角也相等的多边形是正多边形

2. 如图，正三角形ABC的外接圆的半径为R，则边长为_____，边心距为_____，面积为_____．

3. 要用圆形铁片截出边长为4 cm的正方形铁片，则选用的圆形铁片的直径最小要      cm.

  4. 已知一个正六边形的边心距为cm，则这个正六边形的周长为         cm.

  5.在同一个圆中，圆的内接正三角形、正方形、正六边形的边长之比为            .

答案：

1.  D

2. ；；

3.

4. 12

5.

自主完成练习，然后集体交流评价.

通过课堂练习及时巩固本节课所学内容，并考查学生的知识应用能力，培养独立完成练习的习惯.

环节五

课堂小结

回顾本节课所讲的内容

通过小结总结回顾本节课学习内容，帮助学生归纳、巩固所学知识.

环节六

布置作业

教科书第106页

练习第1、2、3题

第108页

习题24.3第1、6题

课后完成练习

通过课后作业，教师能及时了解学生对本节课知识的掌握情况，以便对教学进度和方法进行适当的调整.