




高中数学3.6 正态分布试讲课ppt课件
展开第二节 正态分布及其应用
正态分布标准正态分布正态分布的应用
根据频数分布表绘制直方图
频数分布逐渐接近正态分布示意图
频数分布图以均数为中心两侧逐渐减少左右基本对称
中间高(均数)两侧逐渐减少完全对称
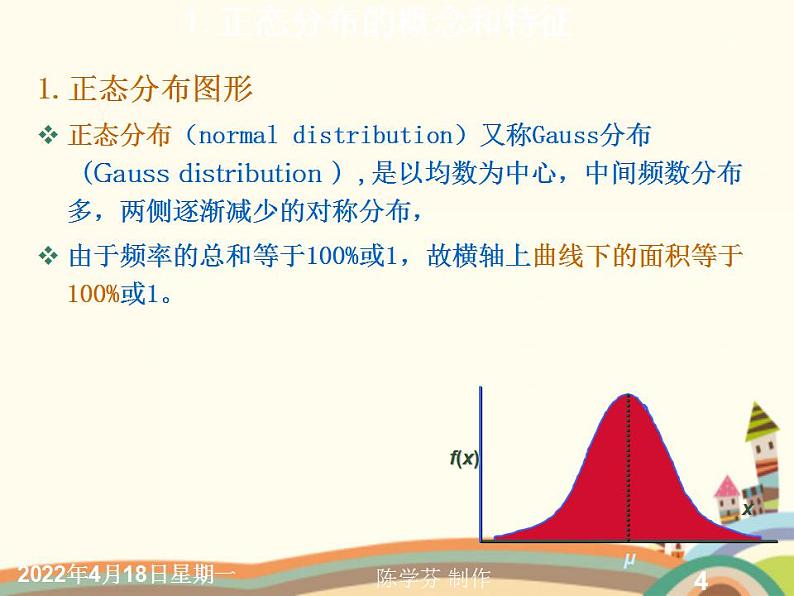
1.正态分布的概念和特征
1.正态分布图形正态分布(nrmal distributin)又称Gauss分布(Gauss distributin ),是以均数为中心,中间频数分布多,两侧逐渐减少的对称分布,由于频率的总和等于100%或1,故横轴上曲线下的面积等于100%或1。
正态分布的密度函数,即正态分布的方程
π、e分别为圆周率和自然对数的底,μ为总体均数,σ为总体标准差 X 为连续随机变量
当x确定后,就可由此式求得其密度函数f(x),即纵坐标的高度了,嘿嘿
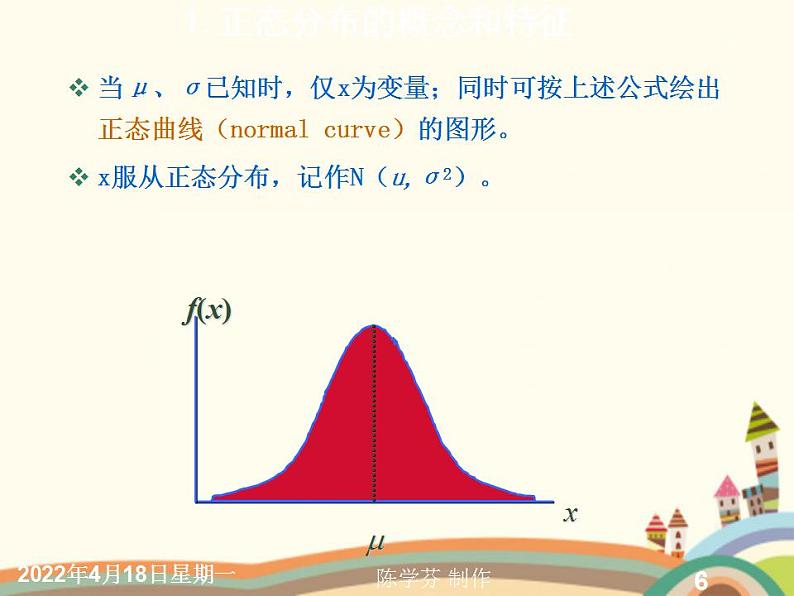
当μ、σ已知时,仅x为变量;同时可按上述公式绘出正态曲线(nrmal curve)的图形。x服从正态分布,记作N(u,σ2)。
正态分布的参数总体均数μ是位置参数 :描述正态分布的集中趋势位置。总体标准差σ是变异度参数:描述正态分布离散趋势, 越小,分布越集中,曲线形状越“瘦高”;反之越“矮胖”。
正态曲线由 两个参数共同决定
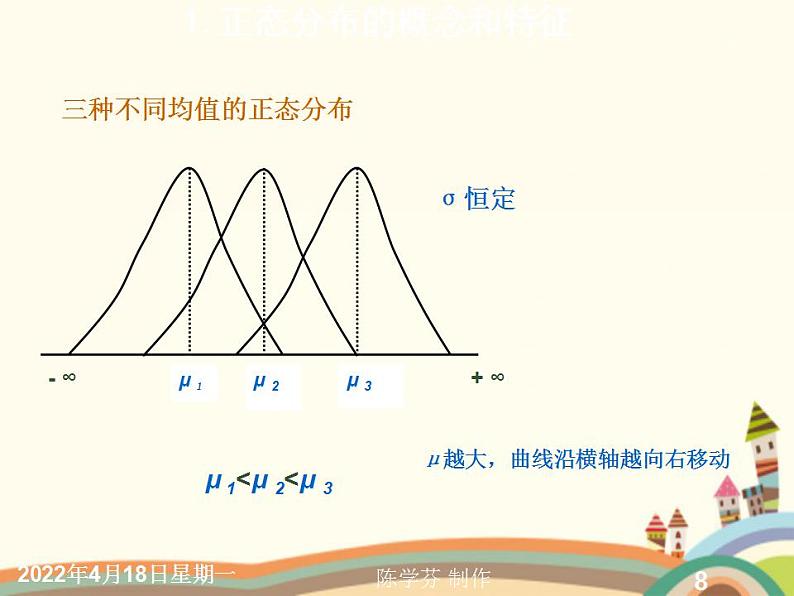
三种不同均值的正态分布
μ 1<μ 2<μ 3
μ越大,曲线沿横轴越向右移动
三种不同标准差的正态分布
σ越大,表示数据越分散,曲线越 “胖”σ越小,表示数据越集中,曲线越 “瘦”
曲线1:μ=2.4, σ=0.8 曲线2:μ=3.4, σ=0.8 曲线3:μ=3.4, σ=1.2
(1) 正态分布以均数μ 为中心,左右对称;(2) 正态曲线(nrmal curve)在横轴上方,且均数所在处最高,X离μ 越远,f(x)越小,逐渐接近0,但不会等于0,故正态曲线永远不与横轴相交;(3) 正态分布的面积分布有一定的规律性,总面积=1;(4) 正态分布有两个参数,即均数与标准差(与)
标准正态分布概率密度函数,记作N(0,1)。
标准正态分布(standard nrmal distributin)
标准正态分布将正态分布曲线的原点移到的位置,横轴尺度以σ为单位,令μ=0,σ=1,则将正态分布变换为标准正态分布
u→±∞Φ (u) →0
一般正态分布为一个分布簇: N(μ, σ2) ;标准正态分布只有一个 N(0,1) ;这样简化了应用。标准正态分布的曲线是唯一的。
2.正态分布的特征(1)正态曲线(nrmal curve)在横轴上方均数处最高 标准正态方程中,u取何值,无论正负,e -u2/2 值均为正,故φ(u)必为正。因此曲线在横轴上方。 式中 为常量,因此u的绝对值越小,则e -u2/2 值越大,u的绝对值最小为0(均数位置),因此该处φ(u)值最大。也就是均数处曲线最高,φ(u)=0.3989
正态分布的特征(2)正态分布以均数为中心,左右对称。式中u为平方,故u值无论正负,只要绝对值相等,则其纵高φ(u)相等,因此正态分布以均数为中心,左右对称。
正态分布的特征(3)正态分布有两个参数,即均数与标准差(与)(4)正态分布的面积分布有一定规律*。
3.正态曲线下面积的分布规律
是正态变量x的累计分布函数,反映正态曲线下,横轴自-∞到x的面积,即下侧累计面积(概率)
标准正态分布曲线下面积
左侧任一区间的面积可以通过对下式积分求得
附表1(P245)就是根据此公式和图形制定的
φ(u)表示从-∞到u值范围内X分布面积
概率密度函数与累积分布函数
标准正态曲线横轴为u值
将变量值(x)转换为u值后,统计学家按φ(u)公式编制成了附表1,即标准正态分布表查表注意事项:1. μ、σ和x已知时,先求出u值,再查表,得所求面积占总面积的比例。 μ、σ未知时,常分别用样本均数和样本标准差来估计。2. 曲线下对称于0的区间,面积相等。比如区间(-∞,-2.58)与区间(2.58,+ ∞)的面积相等。因为附表只列出φ(-u)值。3. 曲线下横轴上的总面积为100%或1。 根据2.3.可以计算上侧累计面积。
例 1.求区间(2.58,+∞)的面积。因为区间(2.58,+∞)和区间(-∞ ,-2.58)对称所以只需求出(-∞ ,-2.58)的面积即可,即查表φ(-2.58)=0.0049φ(-u)对应的u值区间是( -∞ ,-u)2.求区间(-∞ ,2.58 )的面积。φ(2.58)=1- φ(-2.58)
医学常用的三个X分布范围及u界值
任意正态分布变量值(X)理论上分布规律
统计中常用尾部面积的u值,记 ,称为u界值。
(双侧) (双侧) (单侧) (单侧)
概括估计变量值频数分布范围例:在例8.1中,n=132, =4.653mml/L,s=0.40066mml/L,试估计95%和99%的频数分布范围。(3.868~5.438,3.619~5.687)制定医学参考值范围控制实验误差:上下警戒限: 上下控制限:
101名正常成年女子的血清总胆固醇 。试估计该总体正常女子血清总胆固醇在4 mml/L以下者的百分比。 假定该资料服从正态分布,将X1=4转换为u值,查正态分布表
标准正态变量(u1)=-0.09 查附表8-1,在表的左侧找到-0.0,在表的上方找到0.09,,两者的相交处为0.4641=46.41%。
该地正常女子血清总胆固醇在4mml/l以下者的百分比为46.41%。
一、医学参考值的意义医学参考值范围(reference ranges)亦称正常值范围,它是指正常人的解剖、生理、生化等各种指标测定值的波动范围正常人是指排除了有关疾病和因素对所研究指标有影响的人,不同于“健康人”由于存在个体差异,正常值并非为常数,而是在一定范围内波动。确定医学参考值范围,不是用该人群样本观察值的极差,而是常用95%或99%的分布范围作为判定正常和异常的参考标准。
第三节 医学参考值范围
二、制定参考值范围的基本步骤从正常人总体中抽样,明确研究的总体统一测定方法控制测量误差;判定是否需分组(性别、年龄)确定参考值范围;根据专业知识决定取单侧还是双侧界值;
单侧下限—过低异常 单侧上限—过高异 双侧---过高/低均异常
二、制定参考值范围的基本步骤 5. 选定合适的百分界限;6. 对资料的分布进行正态性检验;7. 根据资料的分布类型选定适当的方法进行参考值范围 的估计。
1、正态分布法2、百分位数法
三、医学参考值范围的计算方法:
三、医学参考值范围的计算方法1.正态分布法应用条件:正态分布或近似正态分布资料 计算 双侧100(1-α)%正常值范围:单侧100(1-α)%正常值范围:双侧95%正常值范围:单侧95%正常值范围:
例2.10 利用例1某地55~58岁健康成人的血糖值,求95%的参考值范围。
解 : 假定该资料服从正态分布,因此采用正态分布法公式 计算双侧95%的参考值范围: 所以该地健康成年人的血糖值95%的参考值范围为3.87~5.44(mml/L)
2. 百分位数法适用于偏态分布资料 双侧95%正常值范围: P2.5~P97.5 单侧95%正常值范围: < P95(上限) 或 > P5(下限)
例如:1.确定白细胞总数的95%参考值范围 由于白细胞数过高过低均为异常,故应分别计算P2.5和P97.52.确定肺活量的95%参考值范围 由于肺活量只过低为异常,故只计算P5 3.确定尿铅的95%参考值范围 由于尿铅只以过高为异常,应计算P95
1.正态分布是一种很重要的连续型分布,不少的医学现象服从正态分布或近似正态分布,或经变量变换转换为正态分布,可按正态分布规律来处理。它也是许多统计方法的理论基础。2.正态分布的特征:(1)曲线在横轴上方,均数处最高(2)以均数为中心,左右对称(3)确定正态分布的两个参数是均数μ和标准差σ
3.正态分布用N(μ,σ2) 表示,为了应用方便,常对变量x作 变换,使μ=0,σ=1,则正态分布转换为标准正态分布,用N(0,1)表示。4.正态曲线下面积的分布有一定规律。理论上μ±1σ,μ±1.96σ和μ±2.58σ区间的面积(观察单位数)各占总面积的(总观察单位数)的68.27%,95%和99%,可用来估计医学参考值范围和质量控制等方面。
一、名词解释1.中位数2.四分位数间距3.标准差4.变异系数5.正态分布
二、是非题1.不论数据呈什么分布,都可以用算术均数和中位数表示其平均水平。( )2.少数几个数据比大多数数据大几百倍,一般不宜用算术均数表示其平均水平。( )3.只要单位相同,用s和用CV来表示两组资料的离散程度,结论是完全一样的。( )4.四分位数间距也是描述连续分布数据离散度的指标。( )5.理论上,对于正态分布资料,总体百分位数的P5~P95和μ±1.96σ范围内都包含95%的变量值。( )
三、最佳选择题1、描述一组偏态分布资料的变异度,以( )指标较好。 A.全距 B.标准差 C.变异系数 D.四分位间距 E.方差2、用均数和标准差可以全面描述( )资料的特征/ A.正偏态分布 B.负偏态分布 C.正态分布 D.对称分布 E.对数正态分布3、各观察值均加(或减)同一数后( )。 A.均数不变,标准差改变 B.均数改变,标准差不变 C.两者均不变 D.两者均改变 E.以上都不对
4、比较身高和体重两组数据变异度大小宜采用( )。 A.变异系数 B.方差 C.极差 D.标准差 E.四分位间距5、偏态分布宜用( )描述其分布的集中趋势。 A.算术均数 B.标准差 C.中位数 D.四分位间距 E.方差6、各观察值同乘以一个不等于0的常数后,( )不变。 A.算术均数 B.标准差 C.几何均数 D.中位数 E.变异系数7、( )分布的资料,均数等于中位数。 A.对数正态 B.正偏态 C.负偏态 D.偏态 E.正态
8、对数正态分布是一种( )分布。(说明:设X变量经Y=lgX变换后服从正态分布,问X变量属何种分布?) A.正态 B.近似正态 C.左偏态 D.右偏态 E.对称9、最小组段无下限或最大组段无上限的频数分布资料,可用( )描述集中趋势。 A.均数 B.标准差 C.中位数 D.四分位间距 E.几何均数10、血清学滴度资料最常用来表示其平均水平的指标是( )。 A.算术均数 B.中位数 C.几何均数 D.变异系数 E.标准差
11、中位数是表示变量值 的指标。 A.平均水平 B.变化范围 C.频数分布 D.相互间差别大小 E.以上都不对12、某项指标仅以过高为异常,且资料呈偏态分布,则其95%的参考值范围为 。 A.≤P95 B.≤P97.5 C.≥P5 D.P2.5~P97.5 E. ≥P2.5
13、在同一总体中随机抽样,样本含量n越大,则理论上 越小。 A.样本标准差s B.中位数 C.标准误 D.第95百分位数 E. .变异系数14、原始数据减去一个不为0的常数后, 。 A.均数不变,标准差变 B.均数变,标准差不变 C.均数和标准差都不变 D.均数和标准差都变 E.以上都不对
15.若X 服从以μ, σ2为均数和方差的正态分布,则X 的95%百分位数即____ A B C D E16、计算平均潜伏期宜用: A.算术均数 B.全距 C.离均差积和 D.中位数 E.变异系数17、正态分布有两个参数μ与σ,_____曲线的形状越扁平。 A. μ越大 B. μ越小 C. σ越大 D. σ越小 E. μ与σ越接近0
18、在医学和卫生学研究中,下面_____不是近似正态分布: A.正常成人的血铅含量 B.正常成人的身高 C.正常成人的红细胞数 D.正常成人的血清总蛋白含量 E.正常成人的脉搏数19、在抽样研究中“总体均数”,“总体标准差”: A.一般是不知道的 B.不知道但可以由样本推论 C.总是知道的 D.是给定的两个已知量 E二者相等
20、对120名大学生的身高进行了测量,每个测量值减去均数所得的差值再除以标准差,所得数值的分布是____ A.正态分布 B.标准正态分布 C.正偏态分布 D.负偏态分布 E.偏态分布21、若一组数据呈正态分布,其中 大于的变量值占____ A.99.5% B.99% C.1% D.0.5% E.5%
四、计算分析题1、根据1999年某地某单位的体检资料,116名正常成年女子的血清甘油三脂(mml/L)测量结果如下表,请据此资料: (1)描述集中趋势应选择何指标?并计算之。 (2)描述离散趋势应选择何指标?并计算之。 (3)求该地正常成年女子血清甘油三脂的95%参考值范围。 (4)试估计该地正常成年女子血清甘油三脂在0.8mml/L以下者及1.5mml/L以下者各占正常女子总人数的百分比。
2、某地微丝蚴血症者42例治疗后7年用间接荧光抗体试验测得抗体滴度如下。求平均抗体滴度。
3、测得某地300名正常人尿汞值,其频数表如下。试计算均数和中位数,何者的代表性较好?并求95%的参考值范围。
300例正常人尿汞值(ug/L)
语文版(中职)拓展模块3.3 古典概率备课ppt课件: 这是一份语文版(中职)拓展模块3.3 古典概率备课ppt课件,共16页。PPT课件主要包含了知识讲解,课堂练习,课堂小结等内容,欢迎下载使用。
高中人教版(中职)第三章概率与统计3.3 正态分布说课ppt课件: 这是一份高中人教版(中职)第三章概率与统计3.3 正态分布说课ppt课件,文件包含人教版中职数学拓展模块33《正态分布》ppt课件ppt、人教版中职数学拓展模块33《正态分布》教案设计doc等2份课件配套教学资源,其中PPT共39页, 欢迎下载使用。
高中数学人教版(中职)拓展模块3.3 正态分布课文ppt课件: 这是一份高中数学人教版(中职)拓展模块3.3 正态分布课文ppt课件,共39页。PPT课件主要包含了更一般的情况概率等内容,欢迎下载使用。












