人教版（中职）基础模块上册1.2 充要条件教学课件ppt

课程

数学

课题

1.2 充要条件

课型

理论

日期

教师

课时

1课时

班级

教材

教具

教学

目标

知识目标

1. 使学生正确理解充分条件、必要条件和充要条件三个概念．

2. 能在判断、论证中灵活运用上述三个概念．

能力目标

1、掌握充分条件、必要条件和充要条件的应用。

2、提高学生对条件与结论的研究与判断，培养思维能力。

情感目标

1、培养学生思维的严密性．

教学

重点

教学重点：正确理解充分条件、必要条件和充要条件三个概念．

解决措施：与学生的生活相结合，多尝试问题解决的方法。

教学

难点

教学难点：正确区分充分条件、必要条件．

解决措施：由易到难，具有层次性。从内涵上引导学生体会复合命题中条件和结论的关系。

教学

方法

本节课采用启发式教学和讲练结合的教学方法，引导学生分析归纳，形成概念．

学习

方法

多思考，多总结，多讨论等

教材

分析

数学是一门公共基础课，可以进一步提高中等职业学校学生的文化科学知识，培养学生的创新精神，实践能力，自主学习的能力和适应社会生活的能力。

教材的设计遵循学生认知的发展规律，在保证科学性的基础上，

降低知识的起点，由已知到未知，由浅入深，由具体到抽象。

     随着现代信息技术的不断发展，数学的教学手段和方法也不断更新。本教材的编写不但落实了“教学大纲”对计算器使用的要求，而且也落实了“教学大纲”对计算机软件的使用要求，意在培养学生的计算机能力和数据处理能力，提升学生对数学的理解。

     教材还尽最大可能地将课堂变成师生共同活动的场所，强调学生的参与。从生活实际问题引入数学概念，利用数学知识解决生活中的实际问题，这样不但让学生的思维活跃起来，积极参与到教学过程中来，而且也激发了学生的学习兴趣，体验数学知识的应用。

教学

环节

教　　学　　主　　要　　内　　容

教学方法

一、组织

教学

2

分钟

提前2分钟进教室提示同学手机静音、准备课堂笔记。检查同学们书籍工具的准备情况，强调课堂纪律，使同学们集中注意力上课，作好本节课考勤。

师生致礼问好！

使同学们形成良好的上课习惯

二、回

顾

复

习

3

分

钟

<回顾>

1、表扬上节课较好的情况（小组分数、作业等）

2、回顾上节课的知识点（采用提问、做题等方式）

对上一节课内容进行简单的回顾，看学生掌握的情况为下面讲新课作基

三、导入

新课

3

分钟

<导入>

情景导入：生活的案件、视频、社会上的热点事件等

问题：判断命题“如果 x＝y，则x2＝y2”是否正确．

四、内

容

讲授25分钟

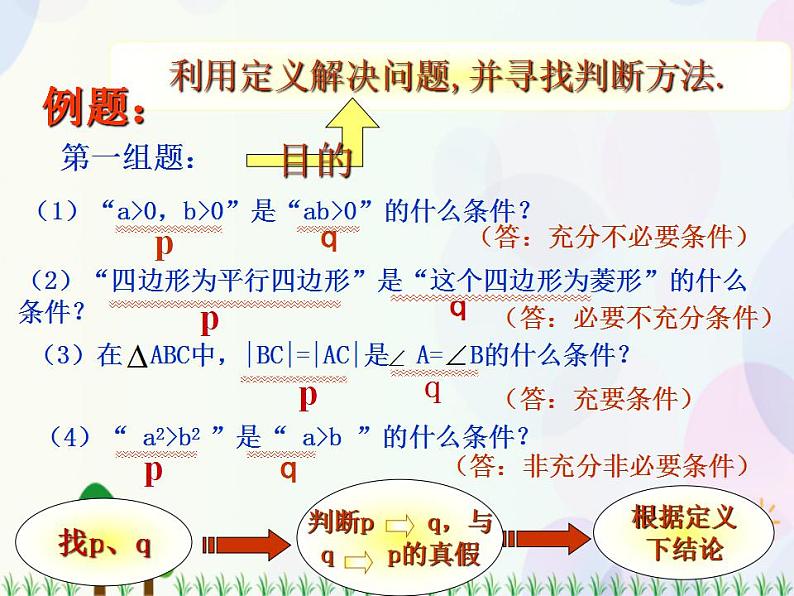
内容：

1．命题与推出．

在数学中，我们经常遇到“如果 p，则 q”形式的命题，这种命题的真假要通过推理来判断．如果p真，证明q也为真，那么“如果p，则q”就是真命题．这时我们就说，由p可推出q．

符号记作：p  q，

读作：“p推出q”．

2．推出与充分、必要条件．

p推出q，通常还可表述为

p是q的充分条件；

q是p的必要条件．

这就是说，

如果p，则q；(真)

p  q；

p是q的充分条件；

q是p的必要条件．

这四句话表达的都是同一意义．

例1  (1)“如果 x＝y，则 x2＝y2”(真)这个命题还可表述为哪几种形式？

(2)“在△ABC中，如果AB＝AC，则∠B＝∠C”(真)这个命题还可表述为哪几种形式？

解  (1)“如果 x＝y，则 x2＝y2”(真)这个命题还可表述为

x＝y  x2＝y2；

或     x＝y 是 x2＝y2 的充分条件；

或     x2＝y2 是 x＝y 的必要条件．

(2)“在△ABC中，如果AB＝AC，则∠B＝∠C”(真)这个命题还可表述为

在△ABC中，AB＝AC∠B＝∠C；

或  在△ABC中，AB＝AC是∠B＝∠C 的充分条件；

或  在△ABC中，∠B＝∠C是AB＝AC 的必要条件．

练习1  教材P22 练习A组第1题．

练习2  教师写出四种等价说法中的一种，学生说出其他三种．

3．充要条件．

观察例1(2)“在△ABC中，如果 AB＝AC，则∠B＝∠C”．

反过来，“在△ABC 中，如果 ∠B＝∠C，则 AB＝AC”这个命题是否正确？若正确，用刚学过的“推出符号”和充分、必要条件怎么叙述?

引出充要条件的概念．

如果p是q的充分条件(p  q )，p又是q的必要条件(q  p )，则称p是q的充分且必要条件，简称充要条件．

记作   p  q．

显然，如果p是q的充要条件，那么q也是p的充要条件．又常说成q当且仅当p，或p与q等价．

例如：两个三角形对应角相等是两个三角形相似的充要条件．

4.综合练习．

例2  用充分条件、必要条件或充要条件填空：

(1) x 是整数是 x 是有理数的   ；

(2) x＝3 是 x2＝9的   ；(3) 同位角相等是两直线平行的            ；

(4) (x－2)(x－3)＝0是 x－2＝0的            ；

练习3  教材 P22，A组第2题．

例3  已知 p 是 q 充分条件，s是 r 必要条件，p 是 s 充要条件．求q与r的关系．

解  根据已知可得

p  q，r  s，p  s．

所以 r  s  p  q．

所以 r  q．

即，r 是 q 的充分条件，q 是 r 的必要条件．

五．随

堂练习

4

分钟

课堂任务练习：

练习1  教师写出四种等价说法中的一种，学生说出其他三种．

练习2  用充分而不必要条件、必要而不充分条件、充要条件、既不充分也不必要条件填空：

(1) a＝b 是 a c＝b c 的       ；

(2) 两个三角形全等是两个三角形相似的            ；

(3) 四边形的对角线相等是四边形是矩形的            ；

(4) a＋5是无理数是 a 是无理数的           

要求：

1、采用分组完成的形式

2、采用比赛的方式

3、记录最后的成绩作为平时成绩

<巡回指导学生>

1、仔细观察学生的步骤并纠正；

2、让做得好的同学示范，带动鼓励周围的同学；

六、课 堂  小 结2分

钟

<小结>

1. 前推后充分．

2. 后推前必要．

3. 互推充要．

4. 不能推，既不充分又不必要．

七、布

置作业

1

分钟

作业：

     课本P15页练习题1.4：第1，2题

要求：

1、作业完成的时间：当天

2、作业的重要性

八、教        学

后

记

九、板  书

设

计

          1.2 充要条件  

1．命题与推出．符号记作：p  q，读作：“p推出q”．

2．推出与充分、必要条件．

p推出q，通常还可表述为

如果p，则q；(真)

p  q；

p是q的充分条件；

q是p的必要条件．

这四句话表达的都是同一意义．

3．充要条件．记作   p  q．