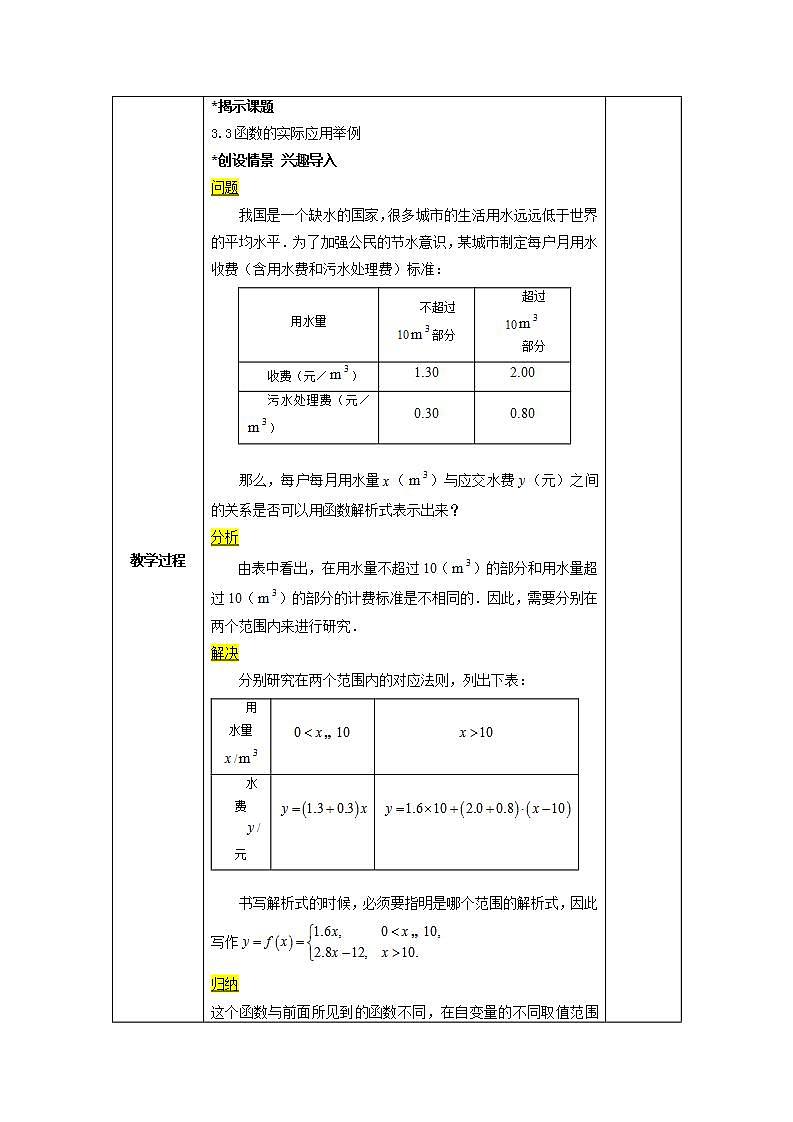
高中数学3.3 函数的应用集体备课课件ppt

这是一份高中数学3.3 函数的应用集体备课课件ppt，文件包含人教版中职数学基础模块上册33《函数的应用》课件ppt、人教版中职数学基础模块上册33《函数的应用》优秀教案docx等2份课件配套教学资源，其中PPT共9页， 欢迎下载使用。

例1 一种商品，如果单价不变，购买8件商品需付120元，写出这种商品件数 x 和总价值 y 之间的函数关系式．
例2 火车从北京站开出12 km后，以80 km/h 匀速行驶．试写出火车总路程 s 与作匀速运动的时间 t 之间的函数关系式．
y = 15x，xN
s = 12 ＋80t，t≥0
(4) 利用函数知识求解(通常是最值问题)；
解函数应用题的一般步骤
(1) 设未知数(确定自变量和函数)；
(2) 找等量关系,列出函数关系式；
(3) 化简,整理成标准形式(一次函数、二次函数等)；
由此可得该函数在 时取最大值,且Smax= ,
例3　某单位计划建筑一矩形围墙．现有材料可筑墙的总长度为 l ,如果要使墙围出的面积最大，问矩形的长、宽各等于多少？
即这个矩形是边长等于 的正
方形时,所围出的面积最大.
有300 m长的篱笆材料，如果利用已有的一面墙（设长度够用）作为一边，围成一块矩形菜地，问矩形的长、宽各为多少时，这块菜地的面积最大？
高到多少时,每天客房的租金收入最高.
解：设提高 x 个2元，则将有10 x 间客房空出，则客房租金总收入为：
由此可得当 x＝10时,ymax＝8 000,即每间租金为20＋10×2＝40元时,每天租金的总收入最高为8 000元．
一家旅社有客房300间,每间房租20元,每天都客满.旅社
欲提高档次,并提高租金.如果每间房租增加2元,客房出
租数会减少10间.不考虑其他因素时,旅社将房间租金提
生产何种档次产品的利润最大
某类产品按质量共分10个档次，生产最低档次每件利润为8元．如果产品每提高一个档次，则利润增加2元．用同样的工时，最低档次产品，每天可生产60件，提高一个档次将减少3件，求生产何种档次的产品所获利润最大．