初中数学苏科版八年级上册3.2 勾股定理的逆定理教课内容ppt课件

这是一份初中数学苏科版八年级上册3.2 勾股定理的逆定理教课内容ppt课件，共11页。PPT课件主要包含了∠A900，∠B900，看谁做得又快又好，整理如下，我会做，提升应用等内容，欢迎下载使用。

下面以a,b,c为边长的三角形是不是直角三角形？如果是那么哪一个角是直角？
(1) a=25 b=20 c=15 ____ _____ ;
(2) a=13 b=14 c=15 ____ _____ ;
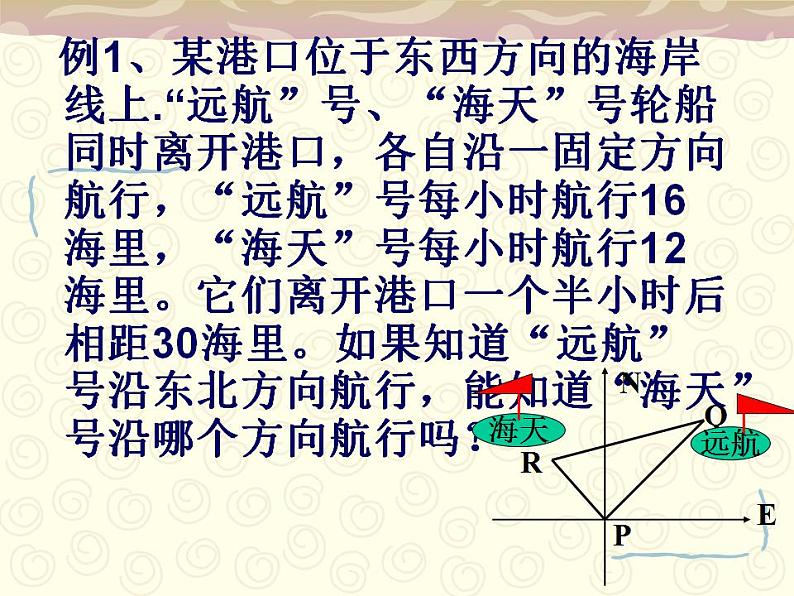
例1、某港口位于东西方向的海岸线上.“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行，“远航”号每小时航行16海里，“海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？
分析：⑴了解方位角，及方位名词；⑵依题意画出图形；⑶依题意可得PR=12×1.5=18，PQ=16×1.5=24， QR=30；⑷因为242+182=302，PQ2+PR2=QR2，所以∠QPR=90°；⑸∠PRS=∠QPR-∠QPS=45°。
注意：已知三边求角，利用勾股定理的逆定理
解：根据题意可得 PR=12×1.5=18， PQ=16×1.5=24， QR=30； 因为242+182=302，即PQ2+PR2=QR2， 根据勾股定理的逆定理知∠QPR=90°； 所以∠PRS=∠QPR-∠QPS=45°。
例2、如图,点A是一个半径为 400 m的圆形森林公园的中心,在森林公园附近有 B .C 两个村庄,现要在 B.C 两村庄之间修一条长为 1000 m 的笔直公路将两村连通,经测得 ∠B=60°,∠C=30°,问此公路是否会穿过该森林公园?请通过计算说明.
1、如果△ABC的三边长分别为 a,b,c,且a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数）则△ABC是直角三角形吗？
解：∵ a=m2-n2,b=2mn,c=m2+n2(m>n,m,n是正整数）
∴a2+b2=(m2-n2)2+(2mn)2
=m4-2m2n2+n4+4m2n2
=m4+2m2n2+n4
∴△ABC是直角三角形。
2．如图，在我国沿海有一艘不明国籍的轮船进入我国海域，我海军甲、乙两艘巡逻艇立即从相距13海里的A、B两个基地前去拦截，六分钟后同时到达C地将其拦截。已知甲巡逻艇每小时航行120海里，乙巡逻艇每小时航行50海里，航向为北偏西40°，问：甲巡逻艇的航向？ 
如图，在正方形ABDC中，E是CD的中点，F为BD上一点，且BF=3FD，求证：∠AEF=90º.
1．性质定理与判定定理之间的关系。2．如何灵活应用勾股定理及逆定理解决实际问题。