冀教版八年级上册13.3 全等三角形的判定精品课后复习题

这是一份冀教版八年级上册13.3 全等三角形的判定精品课后复习题，共19页。试卷主要包含了如图，线段AD、BC相交于点O，如图，若∠1＝∠2，则等内容，欢迎下载使用。


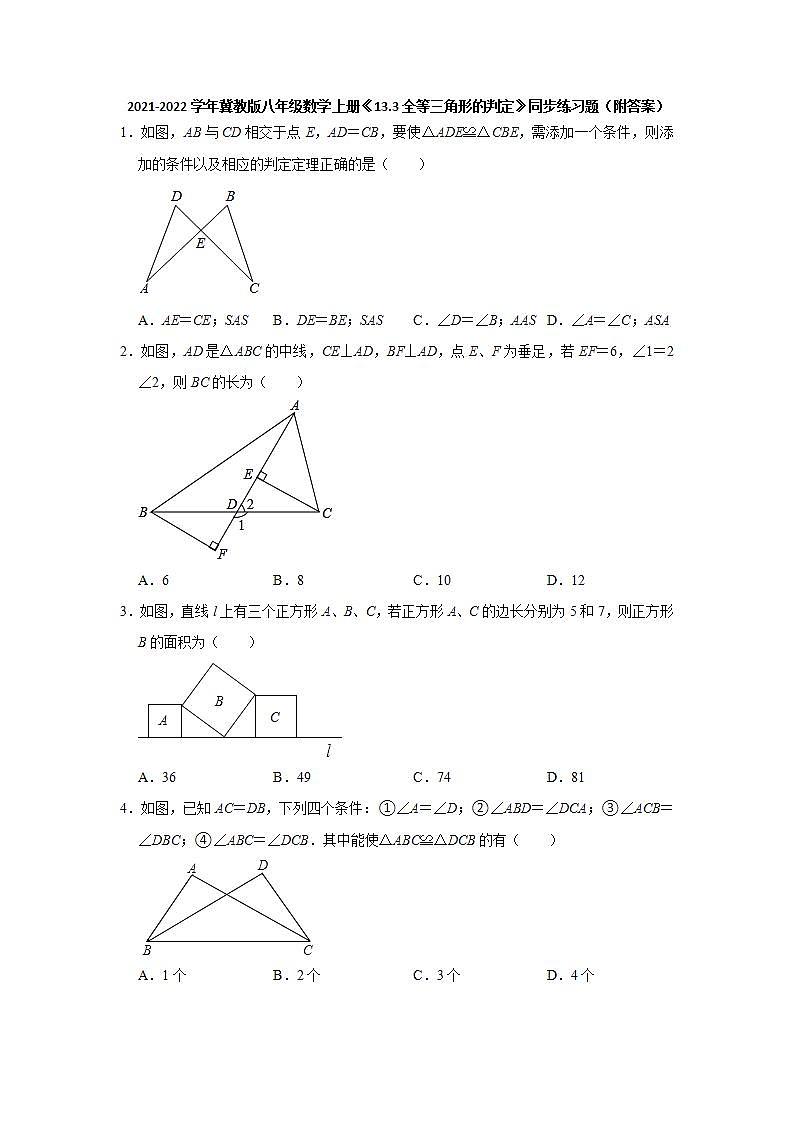
A．AE＝CE；SASB．DE＝BE；SASC．∠D＝∠B；AASD．∠A＝∠C；ASA
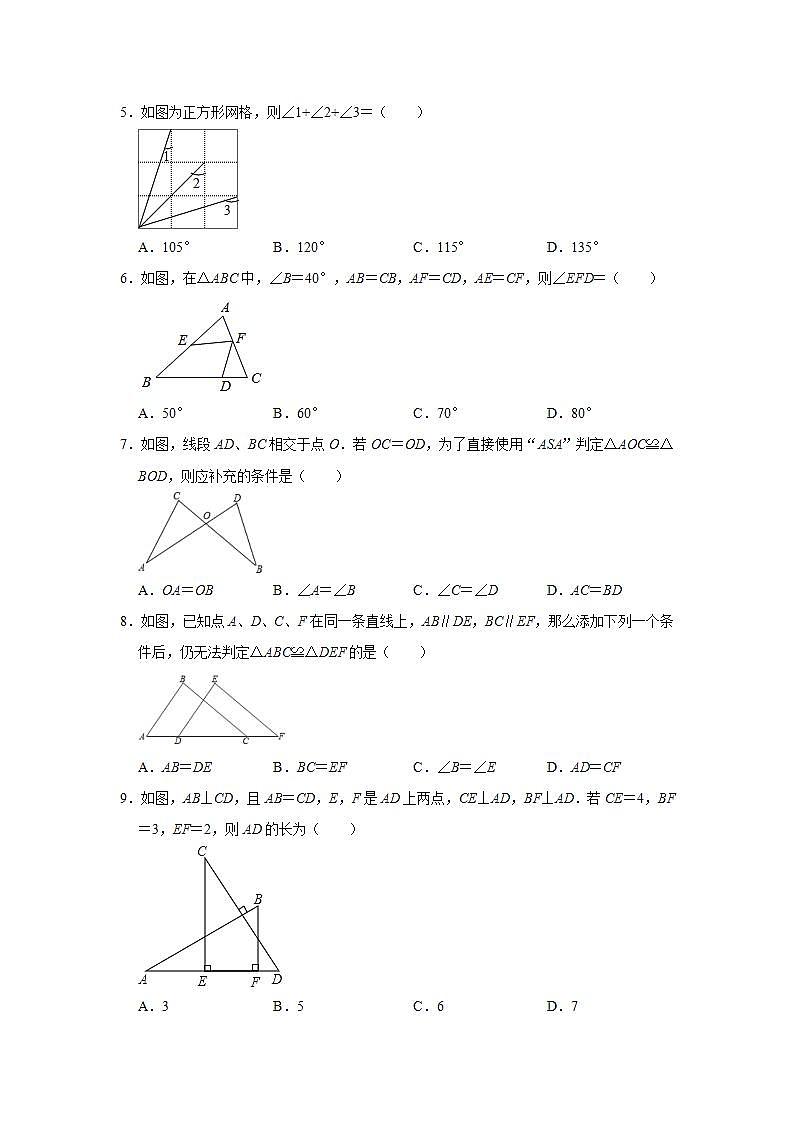
2．如图，AD是△ABC的中线，CE⊥AD，BF⊥AD，点E、F为垂足，若EF＝6，∠1＝2∠2，则BC的长为（ ）
A．6B．8C．10D．12
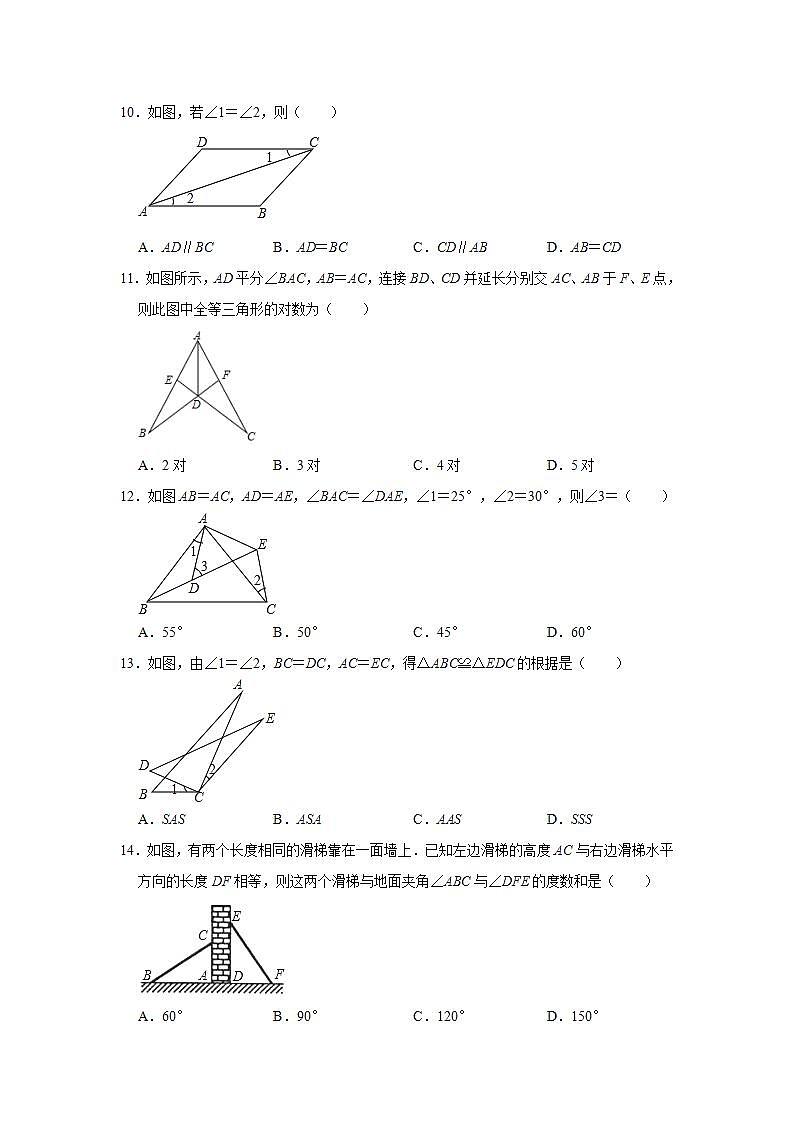
3．如图，直线l上有三个正方形A、B、C，若正方形A、C的边长分别为5和7，则正方形B的面积为（ ）
A．36B．49C．74D．81
4．如图，已知AC＝DB，下列四个条件：①∠A＝∠D；②∠ABD＝∠DCA；③∠ACB＝∠DBC；④∠ABC＝∠DCB．其中能使△ABC≌△DCB的有（ ）
A．1个B．2个C．3个D．4个
5．如图为正方形网格，则∠1+∠2+∠3＝（ ）
A．105°B．120°C．115°D．135°
6．如图，在△ABC中，∠B＝40°，AB＝CB，AF＝CD，AE＝CF，则∠EFD＝（ ）
A．50°B．60°C．70°D．80°
7．如图，线段AD、BC相交于点O．若OC＝OD，为了直接使用“ASA”判定△AOC≌△BOD，则应补充的条件是（ ）
A．OA＝OBB．∠A＝∠BC．∠C＝∠DD．AC＝BD
8．如图，已知点A、D、C、F在同一条直线上，AB∥DE，BC∥EF，那么添加下列一个条件后，仍无法判定△ABC≌△DEF的是（ ）
A．AB＝DEB．BC＝EFC．∠B＝∠ED．AD＝CF
9．如图，AB⊥CD，且AB＝CD，E，F是AD上两点，CE⊥AD，BF⊥AD．若CE＝4，BF＝3，EF＝2，则AD的长为（ ）
A．3B．5C．6D．7
10．如图，若∠1＝∠2，则（ ）
A．AD∥BCB．AD＝BCC．CD∥ABD．AB＝CD
11．如图所示，AD平分∠BAC，AB＝AC，连接BD、CD并延长分别交AC、AB于F、E点，则此图中全等三角形的对数为（ ）
A．2对B．3对C．4对D．5对
12．如图AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝（ ）
A．55°B．50°C．45°D．60°
13．如图，由∠1＝∠2，BC＝DC，AC＝EC，得△ABC≌△EDC的根据是（ ）
A．SASB．ASAC．AASD．SSS
14．如图，有两个长度相同的滑梯靠在一面墙上．已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是（ ）
A．60°B．90°C．120°D．150°
15．如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，有下列结论：①CD＝ED；②AC+BE＝AB；③∠BDE＝∠BAC；④AD平分∠CDE；⑤S△ABD：S△ACD＝AB：AC，其中正确的有（ ）
A．5个B．4个C．3个D．2个
16．如图，已知∠ABC＝∠DCB，要使△ABC≌△DCB，只需要添加一个条件是（ ）
A．∠ABC＝∠ACBB．∠DCB＝∠DC．AC＝BCD．AB＝DC
17．如图，已知∠ABC＝∠DCB，添加以下条件，不能使△ABC≌△DCB的是（ ）
A．AB＝DCB．∠A＝∠DC．AC＝DBD．∠ACB＝∠DBC
18．如图，EB交AC于点M，交FC于点D，AB交FC于点N，∠E＝∠F＝90°，∠B＝∠C，AE＝AF，给出下列结论：其中正确的结论有（ ）
①∠1＝∠2； ②BE＝CF；
③△ACN≌△ABM；
④CD＝DN；
⑤△AFN≌△AEM．
A．2个B．3个C．4个D．5个
19．如图，已知△ABC，下面甲、乙、丙、丁四个三角形中，与△ABC全等的是（ ）
A．B．C．D．
20．如图，AC、BD相交于点E，AB＝DC，AC＝DB，则图中有全等三角形（ ）
A．1对B．2对C．3对D．4对
21．如图，在△ABC中，点D、E、F分别是BC、AB、AC上的点，若AB＝AC，BE＝CD，BD＝CF，∠EDF＝54°，则∠A的度数为（ ）
A．54°B．72°C．80°D．108°
22．如图，在△ABC中，∠A＝90°，DE⊥BC，垂足为E．若AD＝DE且∠C＝50°，则∠ABD＝ °．
23．如图，在△ABC和△DBC中，∠ACB＝∠DBC＝90°，E是BC的中点，DE⊥AB，垂足为点F，且AB＝DE．若BD＝8cm，则AC的长为 ．
24．如图，已知∠1＝∠2，请你添加一个条件 ，使得△ABD≌△ACD．（添一个即可）
25．如图，点B在AE上，∠CBE＝∠DBE，要使△ABC≌△ABD，还需添加一个条件是 （填上适当的一个条件即可）
26．如图所示，AB＝AC，AD＝AE，∠BAC＝∠DAE，∠1＝25°，∠2＝30°，则∠3＝ ．
27．如图，点C，A，O，B四点在同一条直线上，点D在线段OE上，且OA＝OD，AC＝DE，连接CD，AE．
（1）求证AE＝CD；
（2）写出∠1，∠2和∠C三者间的数量关系，并说明理由．
28．王强同学用10块高度都是2cm的相同长方体小木块，垒了两堵与地面垂直的木墙，木墙之间刚好可以放进一个等腰直角三角板（AC＝BC，∠ACB＝90°），点C在DE上，点A和B分别与木墙的顶端重合，求两堵木墙之间的距离．
29．在△ABC中，AD⊥BC于点D，点E为AD上一点，连接CE，CE＝AB，ED＝BD．
（1）求证：△ABD≌△CED；
（2）若∠ACE＝22°，则∠B的度数为 ．
30．如图，△ABF中，E是边AF的中点，点C在BF上，作AD∥BF交CE的延长线于点D．
（1）求证：△ADE≌△FCE．
（2）若∠CEF＝90°，AD＝5，CE＝4，求点E到BF的距离．
参考答案
1．解：A．添加的条件不能推出△ADE≌△CBE，故本选项不符合题意；
B．添加的条件不能推出△ADE≌△CBE，故本选项不符合题意；
C．∵在△ADE和△CBE中，
，
∴△ADE≌△CBE（AAS），故本选项符合题意；
D．∵在△ADE和△CBE中，
，
∴△ADE≌△CBE（AAS），故本选项不符合题意；
故选：C．
2．解：∵∠1＝2∠2，∠1+∠2＝180°，
∴∠2＝60°，
∴∠DCE＝30°，
∵AD是△ABC的中线，
∴BD＝CD，
∵CE⊥AD，BF⊥AD，
∴∠BFD＝∠CED＝90°，
∵∠BDF＝∠CDE，
∴△BFD≌△CED（AAS），
∴DE＝DF，
∵EF＝6，
∴DE＝DF＝3，
∴CD＝6，
∴BC＝12，
故选：D．
3．解：如图，
根据正方形的性质得出∠EFG＝∠EGH＝∠HMG＝90°，EG＝GH，
∵∠FEG+∠EGF＝90°，∠EGF+∠HGM＝90°，
∴∠FEG＝∠HGM，
在△EFG和△GMH中，
，
∴△EFG≌△GMH（AAS），
∴FG＝MH，GM＝EF，
∵正方形A，C的边长分别为5和7，
∴EF2＝52＝25，HM2＝72＝49，
∴B的面积为EG2＝EF2+FG2＝EF2+HM2＝25+49＝74，
故选：C．
4．解：根据SAS，条件③，可以使得△ABC≌△DCB，
故选：A．
5．解：∵在△ABC和△AEF中，，
∴△ABC≌△AEF（SAS），
∴∠4＝∠3，
∵∠1+∠4＝90°，
∴∠1+∠3＝90°，
∵AD＝MD，∠ADM＝90°，
∴∠2＝45°，
∴∠1+∠2+∠3＝135°，
故选：D．
6．解：∵∠B＝40°，AB＝CB，
∴∠A＝∠C＝（180°﹣40°）＝70°，
在△AEF和△CFD中，
，
∴△AEF≌△CFD（SAS），
∴∠AFE＝∠CDF，
∵∠AFE+∠EFD+∠CFD＝180°，∠C+∠CDF+∠CFD＝180°，
∴∠EFD＝∠C＝70°．
故选：C．
7．解：∵CO＝DO，∠AOC＝∠BOD，
∴当∠C＝∠D时，△AOC≌△BOD（ASA），
故选：C．
8．解：A、添加AB＝DE可用AAS进行判定，故本选项错误；
B、添加BC＝EF可用AAS进行判定，故本选项错误；
C、添加∠B＝∠E不能判定△ABC≌△DEF，故本选项正确；
D、添加AD＝CF，得出AC＝DF，然后可用ASA进行判定，故本选项错误；
故选：C．
9．解：∵AB⊥CD，CE⊥AD，BF⊥AD，
∴∠AFB＝∠CED＝90°，∠A+∠D＝90°，∠C+∠D＝90°，
∴∠A＝∠C，∵AB＝CD，
∴△ABF≌△CDE（AAS），
∴AF＝CE＝4，BF＝DE＝3，
∵EF＝2，
∴AD＝AF+DF＝4+（3﹣2）＝5，
故选：B．
10．解：如图，若∠1＝∠2，则CD∥AB；
故选：C．
11．解：图中全等三角形的对数有4对，有△ADB≌△ADC，△ABF≌△ACE，△AED≌△AFD，△EDB≌△FDC，
理由是：∵AD平分∠BAC，
∴∠BAD＝∠CAD，
在△ADB和△ADC中
∴△ADB≌△ADC（SAS），
∴∠B＝∠C，∠ADB＝∠ADC，
∵∠EDB＝∠FDC，
∴∠ADB﹣∠EDB＝∠ADC﹣∠FDC，
∴∠ADE＝∠ADF，
在△AED和△AFD中
∴△AED≌△AFD（ASA），
∴AE＝AF，
在△ABF和△ACE中
∴△ABF≌△ACE（SAS），
∵AB＝AC，AE＝AF，
∴BE＝CF，
在△EDB和△FDC中
∴△EDB≌△FDC（AAS），
故选：C．
12．解：∵∠BAC＝∠DAE，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
∴∠1＝∠EAC，
在△BAD和△EAC中，，
∴△BAD≌△EAC（SAS），
∴∠2＝∠ABD＝30°，
∵∠1＝25°，
∴∠3＝∠1+∠ABD＝25°+30°＝55°，
故选：A．
13．解：∵∠1＝∠2，
∴∠1+∠DCA＝∠2+∠DCA，
即∠BCA＝∠DCE，
在△ABC和△ECD中
，
∴△ABC≌△ECD（SAS），
故选：A．
14．解：∵滑梯、墙、地面正好构成直角三角形，
∵BC＝EF，AC＝DF，
∴Rt△ABC≌Rt△DEF，
∴∠2＝∠3，∠1＝∠4，
∵∠3+∠4＝90°，
∴∠ABC+∠DFE＝90°．
故选：B．
15．解：①正确，因为角平分线上的点到两边的距离相等知；
②正确，因为由HL可知△ADC≌△ADE，所以AC＝AE，即AC+BE＝AB；
③正确，因为∠BDE和∠BAC都与∠B互余，根据同角的补角相等，所以∠BDE＝∠BAC；
④正确，因为由△ADC≌△ADE可知，∠ADC＝∠ADE，所以AD平分∠CDE；
⑤正确，因为CD＝ED，△ABD和△ACD的高相等，所以S△ABD：S△ACD＝AB：AC．
所以正确的有五个，故选：A．
16．解：A、根据∠ABC＝∠DCB，BC＝CB和∠ABC＝∠ACB不能推出△ABC≌△DCB，故本选项不符合题意；
B、根据∠DCB＝∠D，BC＝CB和∠ABC＝∠ACB不能推出△ABC≌△DCB，故本选项不符合题意；
C、根据∠AC＝BC，BC＝CB和∠ABC＝∠ACB不能推出△ABC≌△DCB，故本选项不符合题意；
D、根据BC＝CB，∠ABC＝∠ACB，AB＝DC能推出△ABC≌△DCB，故本选项符合题意；
故选：D．
17．解：∵∠ABC＝∠DCB，BC＝CB，
要使得△ABC≌△DCB，
可以添加：∠A＝∠D，AB＝DC，∠ACB＝∠DBC，
故选：C．
18．解：∵∠E＝∠F＝90°，∠B＝∠C，AE＝AF，
∴△ABE≌△ACF（AAS），
∴BE＝CF，AF＝AE，故②正确，
∠BAE＝∠CAF，
∠BAE﹣∠BAC＝∠CAF﹣∠BAC，
∴∠1＝∠2，故①正确，
∵△ABE≌△ACF，
∴AB＝AC，
又∠BAC＝∠CAB，∠B＝∠C
△ACN≌△ABM（ASA），故③正确，
CD＝DN不能证明成立，故④错误
∵∠1＝∠2，∠F＝∠E，AF＝AE，
∴△AFN≌△AEM（ASA），故⑤正确，
故选：C．
19．解：在△ABC中，∠B＝180°﹣58°﹣72°＝50°，
根据“SAS”可判断图甲的三角形与△ABC全等．
故选：A．
20．解：∵AB＝DC，AC＝DB，BC＝CB，
∴△ABC≌△DCB（SSS），△ABD≌△DCA（SSS），
∴∠BAC＝∠CDB，
∵AB＝CD，∠AEB＝∠DEC，
∴△ABE≌△DCE（AAS）．
故选：C．
21．解：∵AB＝AC，
∴∠B＝∠C，
在△BDE和△CFD中
，
∴△BDE≌△CFD（SAS），
∴∠BED＝∠CDF，∠BDE＝∠CFD，
∴∠BED+∠BDE＝∠CDF+∠CFD，
∵∠BED+∠BDE+∠B＝∠CDF+∠CFD+∠EDF＝180°，
∴∠B＝∠EDF＝54°，
∴∠A＝180°﹣2×54°＝72°，
故选：B．
22．解：∵∠C＝50°，∠A＝90°，
∴∠ABC＝40°，
∵DE⊥BC，
∴∠A＝∠BED＝90°，
在Rt△ABD和Rt△EBD中，
，
∴Rt△ABD≌Rt△EBD（HL），
∴∠ABD＝∠DBE，
∴∠ABD＝∠ABC＝20°，
故答案为：20．
23．解：∵DE⊥AB，可得∠BFE＝90°，
∴∠ABC+∠DEB＝90°，
∵∠ACB＝90°，
∴∠ABC+∠A＝90°，
∴∠A＝∠DEB，
在△ABC和△EDB中，
，
∴△ABC≌△EDB（AAS），
∴BD＝BC，AC＝BE，
∵E是BC的中点，BD＝8cm，
∴BE＝BC＝BD＝4cm．
故答案为：4cm
24．解：添加AB＝AC，
∵在△ABD和△ACD中，
∴△ABD≌△ACD（SAS），
故答案为：AB＝AC．
25．解：BC＝BD，
理由是：∵∠CBE＝∠DBE，∠CBE+∠ABC＝180°，∠DBE+∠ABD＝180°，
∴∠ABC＝∠ABD，
在△ABC和△ABD中
∴△ABC≌△ABD，
故答案为：BC＝BD．
26．解：∵∠BAC＝∠DAE，
∴∠BAC﹣∠DAC＝∠DAE﹣∠DAC，
∴∠1＝∠EAC，
在△BAD和△CAE中，
∴△BAD≌△CAE（SAS），
∴∠2＝∠ABD＝30°，
∵∠1＝25°，
∴∠3＝∠1+∠ABD＝25°+30°＝55°，
故答案为：55°．
27．（1）证明：∵OA＝OD，AC＝DE，
∴OC＝OE，
在△AOE和△DOC中，
，
∴△AOE≌△DOC（SAS），
∴AE＝CD；
（2）解：∠2＝∠1+∠C，理由：
∵△AOE≌△DOC，
∴∠C＝∠E，
∵∠2＝∠1+∠E，
∴∠2＝∠1+∠C．
28．解：由题意得：AC＝BC，∠ACB＝90°，AD⊥DE，BE⊥DE，
∴∠ADC＝∠CEB＝90°，
∴∠ACD+∠BCE＝90°，∠ACD+∠DAC＝90°，
∴∠BCE＝∠DAC，
在△ADC和△CEB中，
，
∴△ADC≌△CEB（AAS）；
由题意得：AD＝EC＝6cm，DC＝BE＝14cm，
∴DE＝DC+CE＝20（cm），
答：两堵木墙之间的距离为20cm．
29．证明：（1）∵AD⊥BC，
∴∠ADB＝∠CDE＝90°，
在Rt△ADB与Rt△CDE中，
，
∴Rt△ADB≌Rt△CDE（HL）；
（2）∵Rt△ADB≌Rt△CDE，
∴AD＝CD，
∴△ADC是等腰直角三角形，
∴∠ACD＝45°，
∴∠ECD＝∠ACD﹣∠ACE＝45°﹣22°＝23°，
∴∠CED＝90°﹣23°＝67°，
∴∠B＝∠CED＝67°，
故答案为：67°．
30．（1）证明：∵AD∥CF，
∴∠D＝∠FCE，
∵E是AF的中点，
∴AE＝EF，
在△ADE和△FCE中，
，
∴△ADE≌△FCE（AAS）．
（2）解：如图，过点E作EH⊥BF于H．
∵△ADE≌△FCE，
∴CF＝AD＝5，
∵∠CEF＝90°，
∴EF＝＝＝3，
∵S△ECF＝•CF•EH＝•EC•EF，
∴EH＝＝．