







数学基础模块上册3.3 函数的实际应用举例精品课件ppt
展开【课题】4.1实数指数幂(1)
【教学目标】
知识目标:
⑴ 复习整数指数幂的知识;
⑵ 了解n次根式的概念;
⑶ 理解分数指数幂的定义.
能力目标:
⑴ 掌握根式与分数指数幂之间的转化;
⑵ 会利用计算器求根式和分数指数幂的值;
⑶ 培养计算工具使用技能.
情感目标:
⑴ 体验计算器带来的便利,享受成功的快乐;
⑵ 经历合作学习的过程,树立团队合作意识.
【教学重点】
分数指数幂的定义.
【教学难点】
根式和分数指数幂的互化.
【教学设计】
⑴ 通过复习二次根式而拓展到n次根式,为分数指数幂的介绍做好知识铺垫;
⑵ 复习整数指数幂知识以做好衔接;
⑶ 利用课件介绍分数指数幂的概念,字母动感闪耀强化位置关系;
⑷ 加大学生动手计算的练习,巩固知识;
⑸ 小组讨论、学习计算器的使用,培养计算工具使用技能.
【教学备品】
教学课件.
【课时安排】
2课时.(90分钟)
【教学过程】
教 学 过 程 | 教师 行为 | 学生 行为 | 教学 意图 | 时间 |
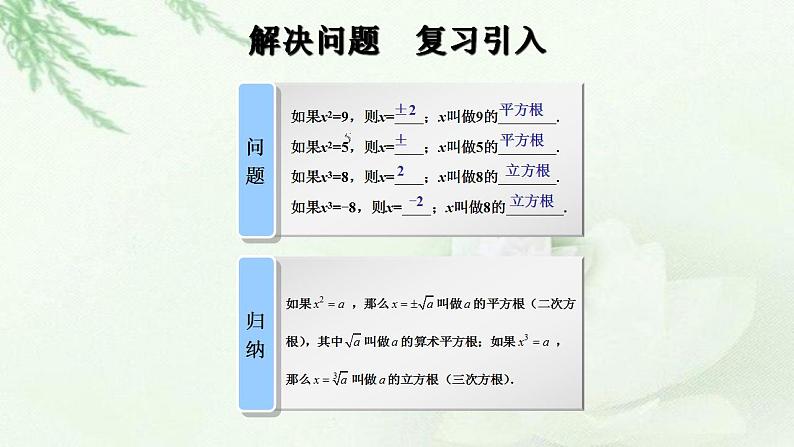
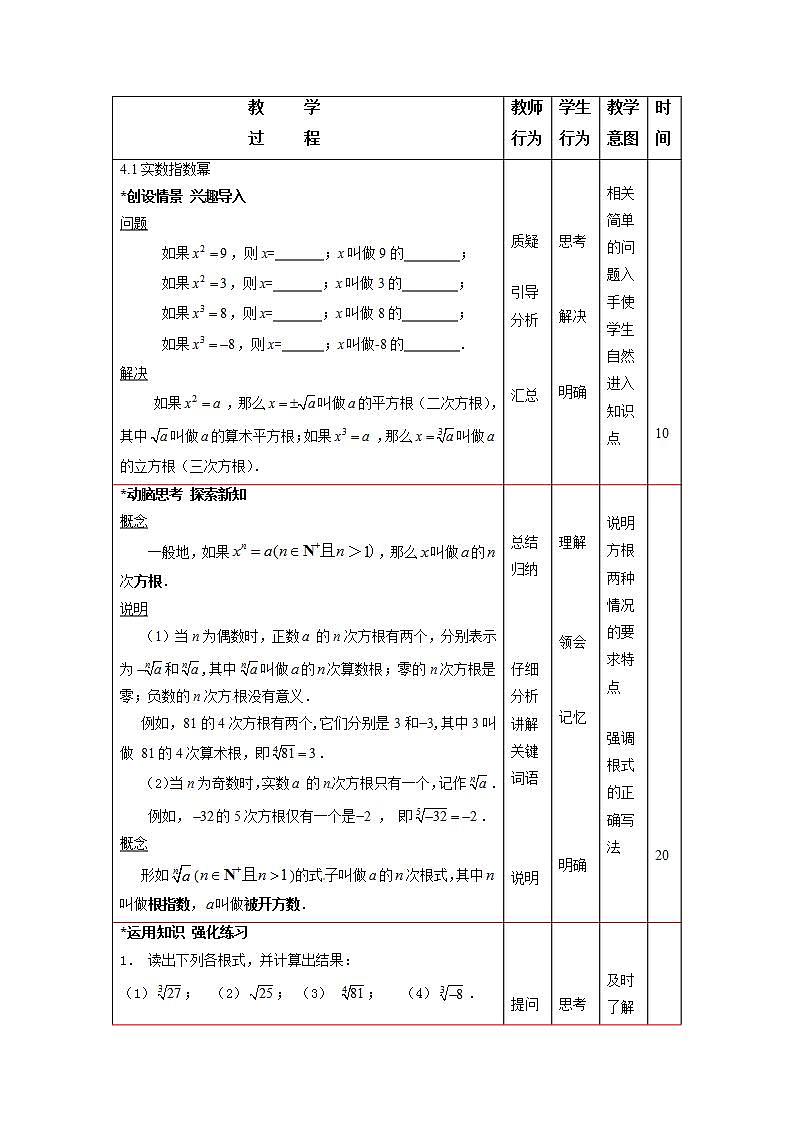
*揭示课题 4.1实数指数幂 *创设情景 兴趣导入 问题 如果,则x= ;x叫做9的 ; 如果,则x= ;x叫做3的 ; 如果,则x= ;x叫做8的 ; 如果,则x= ;x叫做-8的 . 解决 如果,那么叫做的平方根(二次方根),其中叫做的算术平方根;如果,那么叫做的立方根(三次方根). |
介绍
质疑
引导 分析
汇总
|
了解
思考
解决
明确 |
相关 简单 的问 题入 手使 学生 自然 进入 知识 点 |
10 |
*动脑思考 探索新知 概念 一般地,如果>,那么叫做的次方根. 说明 (1)当n为偶数时,正数的n次方根有两个,分别表示为和,其中叫做的次算数根;零的n次方根是零;负数的n次方根没有意义. 例如,81的4次方根有两个,它们分别是3和−3,其中3叫做 81的4次算术根,即. (2)当n为奇数时,实数的n次方根只有一个,记作. 例如,的5次方根仅有一个是−2 , 即. 概念 形如()的式子叫做的次根式,其中叫做根指数,叫做被开方数. |
总结 归纳
仔细 分析 讲解 关键 词语
说明 |
理解
领会
记忆
明确 | [来源:
说明 方根 两种 情况 的要 求特 点
强调 根式 的正 确写 法 |
20 |
*运用知识 强化练习 1. 读出下列各根式,并计算出结果: (1); (2); (3) ; (4). 2. 填空: (1)25的3次方根可以表示为 ,其中根指数为 ,被开方数为 ; (2)12的4次算术根可以表示为 ,其中根指数为 ,被开方数为 ; (3)-7的5次方根可以表示为 ,其中根指数为 ,被开方数为 ; (4)8的平方根可以表示为 ,其中根指数为 ,被开方数为 . |
提问
巡视
指导
答疑 |
思考
动手 求解
交流 |
及时 了解 学生 知识 掌握 情况
出现 的问 题明 确强 调 |
30 |
*自我探索 使用工具 准备计算器. 观察计算器上的按键并阅读相关的使用说明书,小组完成计算器计算根式的方法. 计算下列各题(精确到0.0001): (1); (2); (3); (4). |
质疑
巡视
汇总 |
小组 讨论
探究 | 计算 器的 使用 方法 教给 学生 自我 研究 |
45 |
*知识回顾 复习导入 问题 计算: = ;= ;= ; = ;= . 解决 整数指数幂,当时,= ; 并且规定当时,= ; = . 探究 将整数指数幂的概念进行推广:= . |
[来源:Z+xx+k.Com]
质疑
引导
分析 说明 |
求解
总结 理解
思考 | 引导 学生 解决[来源:Z。xx。k.Com] 整数 指数 幂问 题并 顺利 过渡 分数 指数 幂 |
[来源:学§科§网]
55 |
*动脑思考 探索新知 概念 规定:,其中>1.当为奇数时,;当为偶数时,. 当有意义,且,>1时,规定: 这样就将整数指数幂推广到有理数指数幂. |
总结 归纳
强调 关键 字母
|
理解
领会
记忆
|
分数 指数 幂的 定义 式重 点要 明确 字母 位置 |
60 |
*巩固知识 典型例题 例1 将下列各分数指数幂写成根式的形式: (1); (2); (3). 分析 要把握好形式互化过程中字母的位置对应关系,按照规定,先正确找出公式中的m与n,再进行形式的转化. 解 (1),,故; (2),,故; (3),,故. 例2 将下列各根式写成分数指数幂的形式: (1); (2); (3). 分析 要把握好形式互化过程中字母位置的对应关系,按照规定逆向进行形式的转化. 解 (1),,故; (2),,故; (3),,故. 说明:将根式写成分数指数幂的形式或将分数指数幂写成根式的形式时,要注意规定中的m、n的对应位置关系,分数指数的分母为根式的根指数,分子为根式中被开方数的指数. |
说明
分析
引领
讲解
质疑
引领
讲解
归纳 强调
|
观察
思考
主动 求解
领会
思考
理解
明确 记忆 |
通过 例题 进一 步明 确分 数指 数幂 的定 义式
注意 观察 学生 是否 掌握 知识 点
可以 交给 学生 自我 总结 |
70 |
*运用知识 强化练习 教材练习4.1.1 1.将下列各根式写成分数指数幂的形式: (1); (2); (3); (4). 2.将下列各分数指数幂写成根式的形式: (1); (2); (3) ; (4). |
提问
巡视[来源:学#科#网]
答疑 指导 |
动手 求解
交流 |
及时 指导 学生 练习 加深 理解 |
75 |
*自我探索 使用工具 准备计算器,观察计算器上的按键并阅读相关的使用说明书,小组完成利用计算器计算分数指数幂的方法. 利用计算器求下列各式的值(精确到0.0001): (1); (2); (3). 练习教材4.1.1 3.利用计算器求下列各式的值(精确到0.0001): (1); (2); (3). |
质疑
巡视
汇总 |
小组 讨论
探究
交流 |
继续 引导 学生 自我 探索 计算 器的 使用 |
80 |
*归纳小结 强化思想 本次课学了哪些内容?重点和难点各是什么?
*自我反思 目标检测 本次课采用了怎样的学习方法? 你是如何进行学习的? 你的学习效果如何? |
引导
提问
|
回忆
反思 交流 | 培养 学生 总结 反思 学习 过程 能力 |
85 |
*继续探索 活动探究 (1)读书部分: 教材章节4.1; (2)书面作业: 学习与训练4.1; (3)实践调查: 了解计算器的其他计算使用方法. |
说明 |
记录 |
|
90 |
中职数学高教版(2021·十四五)基础模块 下册5.1 实数指数幂完美版ppt课件: 这是一份中职数学高教版(2021·十四五)基础模块 下册5.1 实数指数幂完美版ppt课件,共35页。PPT课件主要包含了有理数指数幂,实数指数幂等内容,欢迎下载使用。
高中数学高教版(中职)基础模块上册4.1.2 实数指数幂及其运算法则一等奖课件ppt: 这是一份高中数学高教版(中职)基础模块上册4.1.2 实数指数幂及其运算法则一等奖课件ppt,文件包含高教版数学基础模块上册42指数函数PPT课件pptx、高教版数学基础模块上册42指数函数教案doc等2份课件配套教学资源,其中PPT共17页, 欢迎下载使用。
高中数学高教版(中职)基础模块上册4.1.2 实数指数幂及其运算法则完整版课件ppt: 这是一份高中数学高教版(中职)基础模块上册4.1.2 实数指数幂及其运算法则完整版课件ppt,文件包含高教版数学基础模块上册412实数指数幂PPT课件pptx、高教版数学基础模块上册412实数指数幂2教案doc等2份课件配套教学资源,其中PPT共18页, 欢迎下载使用。












