2021学年1.4 集合的运算课前预习课件ppt

这是一份2021学年1.4 集合的运算课前预习课件ppt，共21页。PPT课件主要包含了复习提问，创境导入，概念感知，概念形成，概念深化，学以致用，自学探究，综合应用，可以用韦恩图表示，全集常用U表示等内容，欢迎下载使用。

真子集：如果集合 A 是集合 B 的子集，并且 B 中　　　　至少有一个元素不属于 A，那么集合 A 　　　　叫做集合 B 的真子集．
1．子集与真子集的区别是什么？
不含任何元素的集合叫做空集．
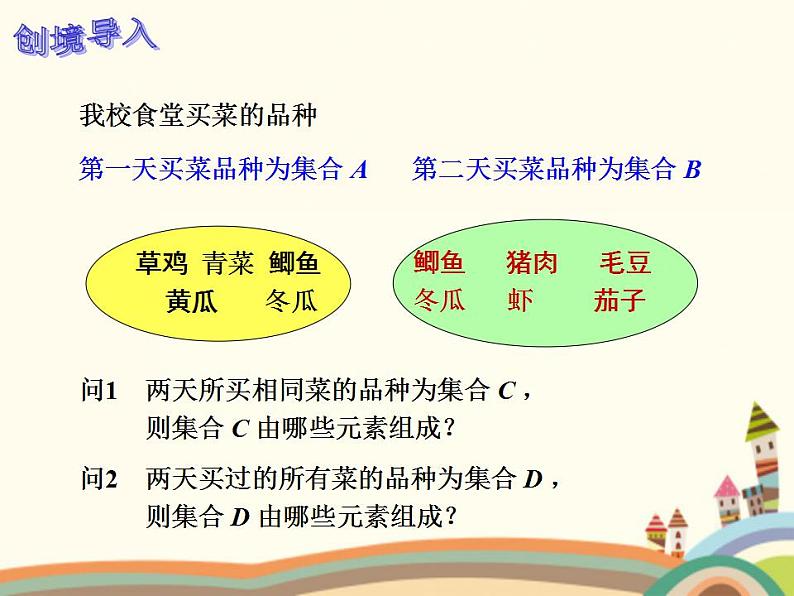
第二天买菜品种为集合 B
第一天买菜品种为集合 A
问1 两天所买相同菜的品种为集合 C ， 则集合 C 由哪些元素组成？问2 两天买过的所有菜的品种为集合 D ， 则集合 D 由哪些元素组成？
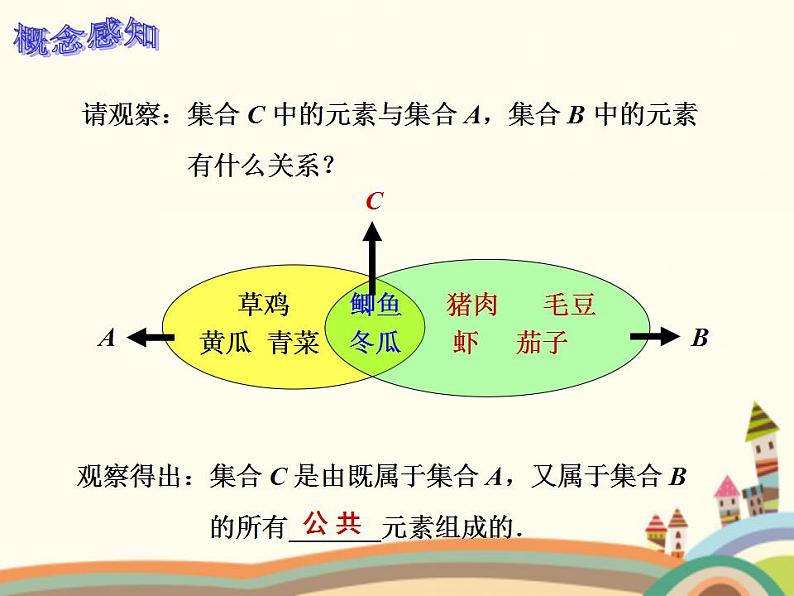
请观察：集合 C 中的元素与集合 A，集合 B 中的元素　　　　　有什么关系？
观察得出：集合 C 是由既属于集合 A，又属于集合 B 的所有 元素组成的．
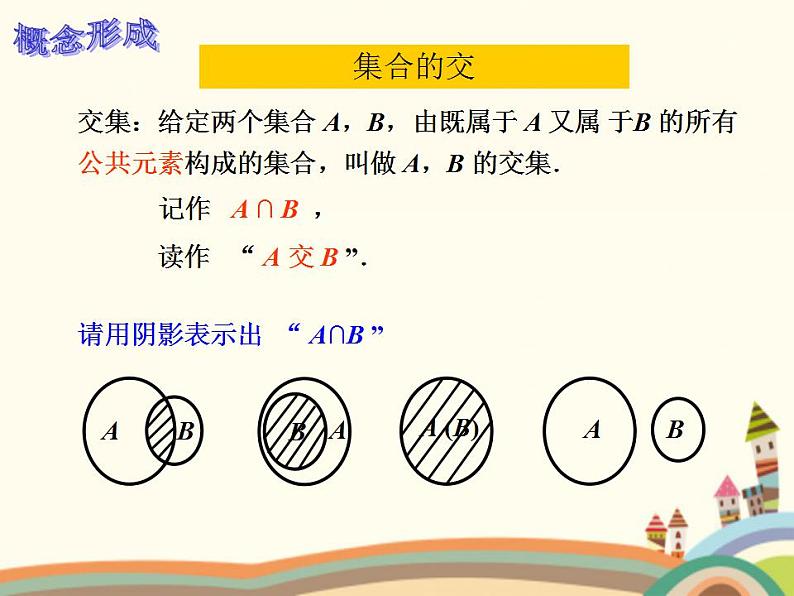
读作 “ A 交 B ”．
交集：给定两个集合 A，B，由既属于 A 又属 于B 的所有公共元素构成的集合，叫做 A，B 的交集．
记作 A ∩ B ，
请用阴影表示出 “ A∩B ”
A B
A B
想一想： 如果 A  B ，那么 A ∩ B = ．
(1) A ∩ B B ∩ A ；(2) ( A ∩ B )∩ C A ∩( B ∩ C )；(3) A ∩ A = ； (4) A ∩  =  A = ；
根据交集的定义和图示，填写交集的性质.
例1 已知：A = {-2,0，3 ，5,8}，B = { -1,0,3，5 }， 求A ∩ B．解： A ∩ B = ；
例2 已知 A = { x | x>0 }，B = { x | x≤1 }， 求 A ∩B．解： A∩ B = ；
{ x︱0＜ x≤1 }
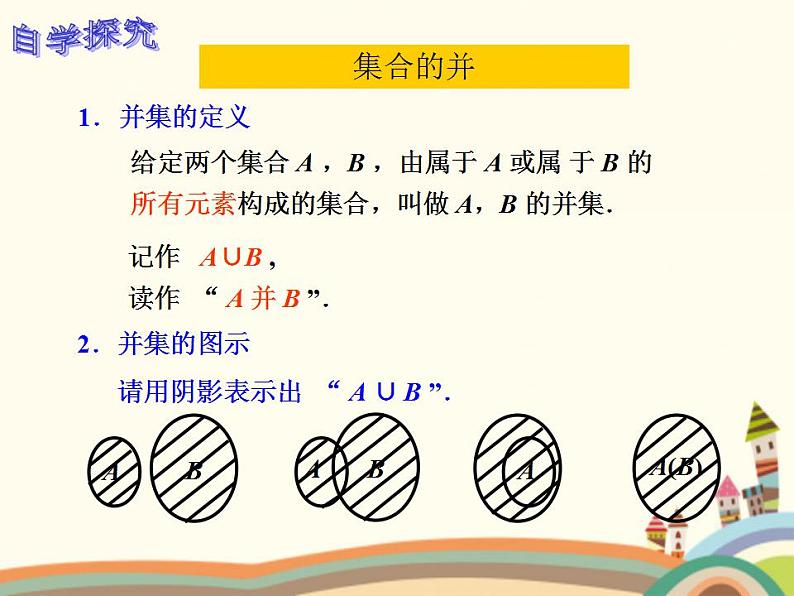
给定两个集合 A ，B ，由属于 A 或属 于 B 的所有元素构成的集合，叫做 A，B 的并集．
记作 A∪B ,读作 “ A 并 B ”．
2．并集的图示 请用阴影表示出 “ A ∪ B ”．
(1) A ∪ B B ∪ A ；(2) ( A ∪ B ) ∪ C A ∪( B ∪ C )；(3) A ∪ A = ；(4) A ∪  =  A = ．
想一想： 如果 A  B ，那么 A ∪ B ＝ ．
例 3 已知： A = {3，4，6,7 }，B = { 2，3，5，7 }， 求 A ∪ B．解 A ∪ B = ；
{ 2，3，4，5 ，6,7}
例4 已知 A = { x | x＜1 }，B = { x | x≥1 }，　　 求 A∩ B．
解：A ∪ B = R．
练习 已知 A = {x | x 是平行四边形}，　　　　　 B = {x | x 是菱形}，　　　求 A∩B； A∪B．
解：A∩B = {x | x 是平行四边形}∩{x | x 是菱形} = {x | x 是菱形} = B； A∪B = {x | x 是平行四边形}∪{x | x 是菱形} = {x | x 是平行四边形} = A．
练习 已知 A = {x | x 是菱形}，B = {x | x 是矩形}， 求 A∩B．
解：A∩B = {x | x 是菱形}∩{x | x 是矩形} = {x | x 是正方形}．
观察下列三个集合：U＝{本班全体同学}A＝{本班所有男同学}B＝{本班所有女同学}
问：这三个集合之间有何关系？
一般的，如果一个集合含有我们所研究问题中涉及的所有元素，那么就称这个集合为全集.
设U是全集,A是U的一个子集,
则由U中所有不属于A的元素组
成的集合叫作U中子集A的补集
例1 设全集U={0,1,2,3,4,5,6,7},A={1,3,5}B={2,4,7},求CUA,CUB.
解:根据题意可知,U={1,2,3,4,5,6,7,0}, 所以 CUA={0,2,4,6,7} CUB={0,1,3,5,6} .
2. 设全集为R,