语文版（中职）基础模块上册6.2 平面向量的运算课前预习ppt课件

这是一份语文版（中职）基础模块上册6.2 平面向量的运算课前预习ppt课件，共14页。PPT课件主要包含了向量的定义，向量的表示，字母表示，几何表示，向量的模与零向量，三种向量关系，相等向量，相反向量，平行的向量，向量的加法等内容，欢迎下载使用。

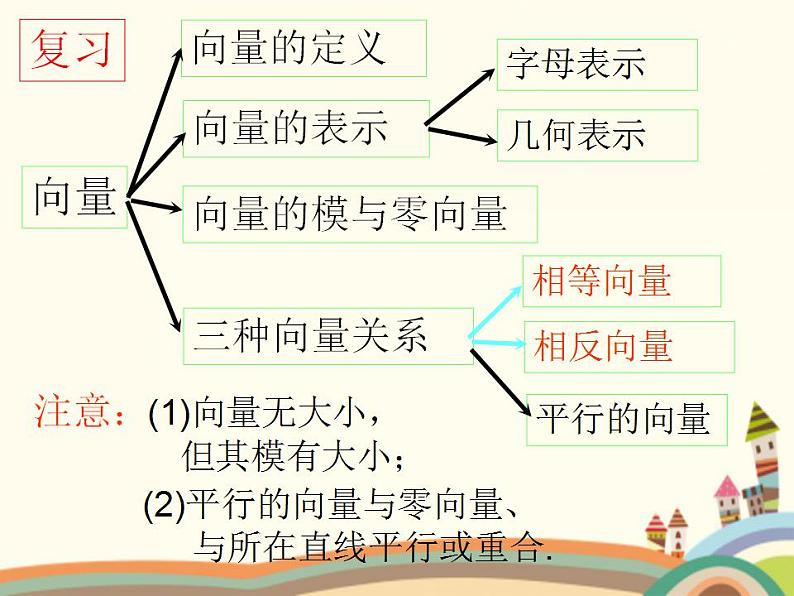
注意：(1)向量无大小， 但其模有大小；
(2)平行的向量与零向量、 与所在直线平行或重合.
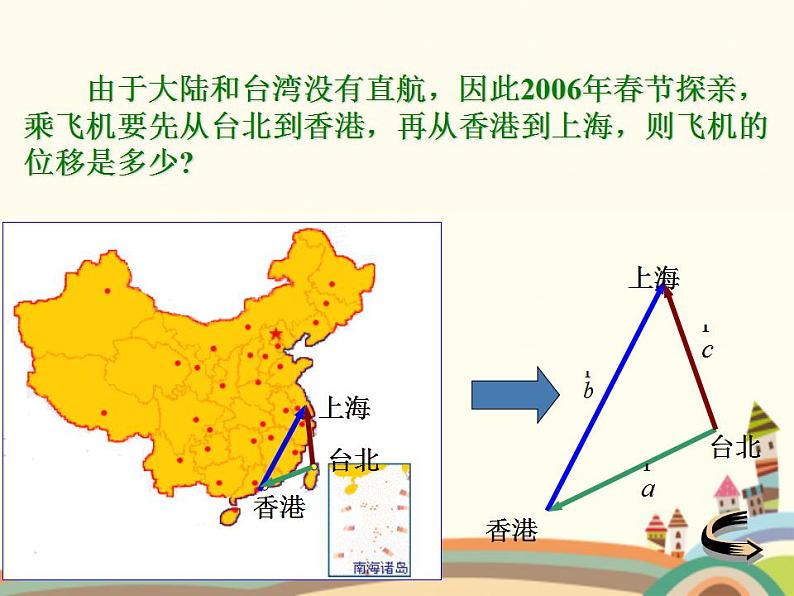
由于大陆和台湾没有直航，因此2006年春节探亲，乘飞机要先从台北到香港，再从香港到上海，则飞机的位移是多少?
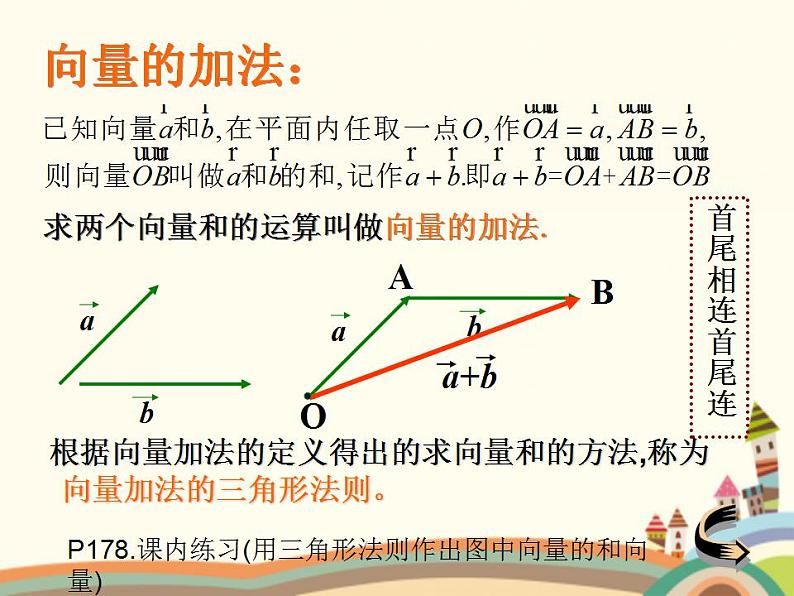
求两个向量和的运算叫做向量的加法.
根据向量加法的定义得出的求向量和的方法,称为
向量加法的三角形法则。
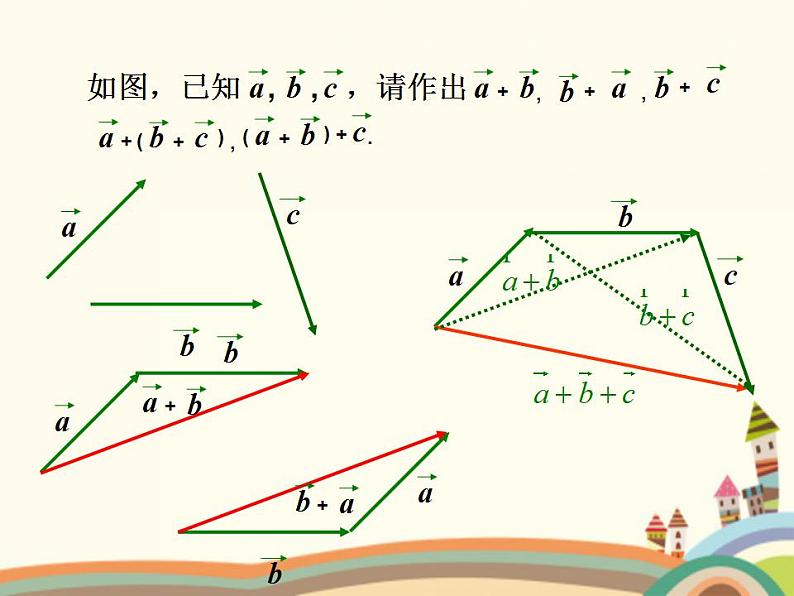
P178.课内练习(用三角形法则作出图中向量的和向量)
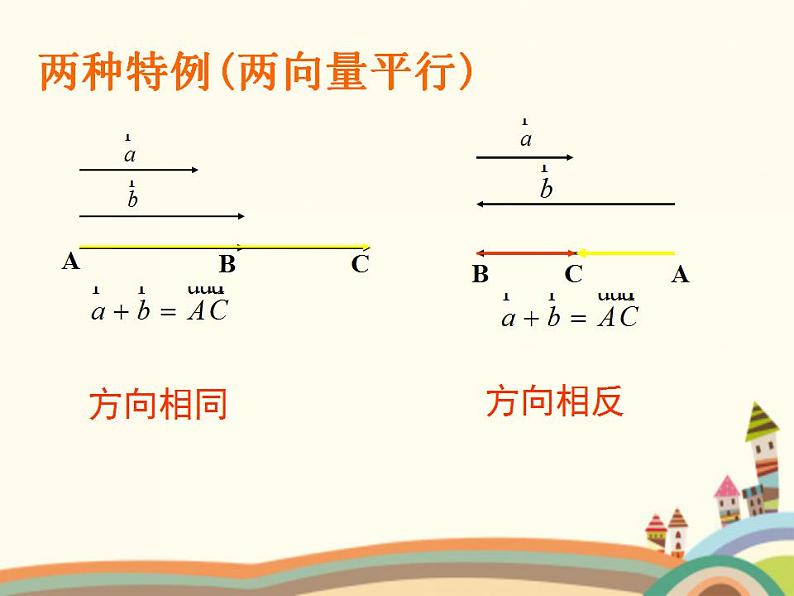
两种特例(两向量平行)
1.若两向量互为相反向量,则它们的和是多少?
向量加法的平行四边形法则
向量加法的平行四边形法则:
以两个向量为邻边构成平行四边形,则以共同起点出发的对角线所在的向量即为这两个向量的和向量.
如图,已知 用向量加法的平行四边形法则作出
三角形法则：将两个向量起点移到同一点处后，若两个向量相减，它们与差向量构成三角形，第三条边所在的向量即为它们的差向量，箭头指向与被减向量一致。
P179.课内练习1课外练习1