2020-2021学年第六单元 平面向量6.4 平面向量的内积教课内容ppt课件

这是一份2020-2021学年第六单元 平面向量6.4 平面向量的内积教课内容ppt课件，共13页。PPT课件主要包含了向量的直角坐标运算，向量的坐标，若向量，特别地，你知道为什么吗，你会求吗等内容，欢迎下载使用。

两个向量和与差的坐标分别等于这两个向量相应坐标的和与差.
实数与向量乘积的坐标等于用这个实数乘以向量相应的坐标.
一个向量的坐标等于向量终点的坐标减去始点的相应坐标．
用向量的坐标表示向量平行的条件
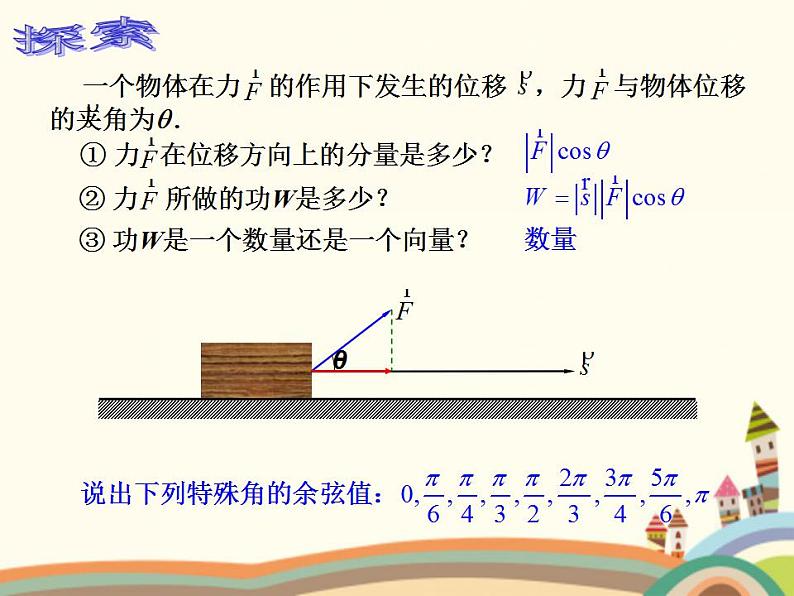
③ 功W是一个数量还是一个向量？
说出下列特殊角的余弦值：
两个非零向量夹角的概念
在两向量的夹角定义中，两向量必须是同起点的．
向量的内积(数量积)的概念
②两个向量的内积是一个实数，不是向量，符号由csθ 的符号所决定．
①这是一种新的运算，以前所学的运算律、 性质是否适用需要验证．
根据向量内积的定义，我们可得到一些常用结论：
可以验证，向量内积满足以下运算律
向量的数量积运算不满足结合律.