2020-2021学年5.1一元一次方程教学演示课件ppt

这是一份2020-2021学年5.1一元一次方程教学演示课件ppt，共29页。PPT课件主要包含了课堂讲解，课时流程，逐点导讲练，课堂小结，作业提升，知识点，方程的定义，①②③⑤⑥⑦，①③⑤⑥⑦，一元一次方程等内容，欢迎下载使用。

方程的定义一元一次方程方程的解列方程
琳琳和李华在玩游戏，琳琳说：“你想一个数，按我告诉你的做，只要你回答结果，我就知道你想的数是几. ”李华说：“好吧！”琳琳：“乘以3，再加上6，结果是？”李华：“18. ”琳琳：“你想的是4. ”李华：“你真神啊，你能告诉我原因吗？”琳琳：“学习这一节，只要认真学习，你会更神奥！”
像2x+4(35－x)=94, 3x+(9－x)=21这样含有未知数的等式叫做方程.
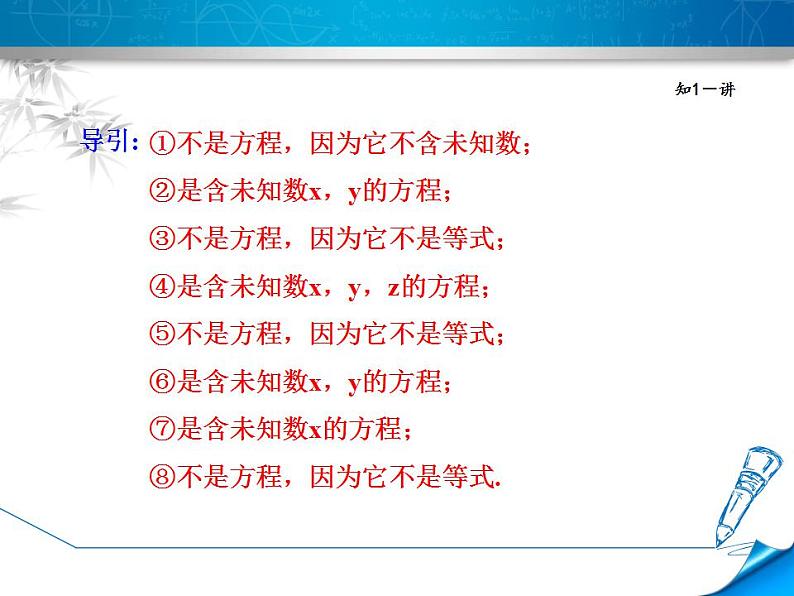
例1 下列式子：①8－7＝1＋0；② x－y＝x2； ③a－b；④6x＋y＋z＝0；⑤x＋2；⑥ ＝3； ⑦x＝5；⑧x－2＞1，其中是方程的有(　　)A．3个　　　B．4个　　　C．5个　　　D．6个
①不是方程，因为它不含未知数；②是含未知数x，y的方程；③不是方程，因为它不是等式；④是含未知数x，y，z的方程；⑤不是方程，因为它不是等式；⑥是含未知数x，y的方程；⑦是含未知数x的方程；⑧不是方程，因为它不是等式.
判断是不是方程，必须紧扣方程的两个要素：等式、未知数，两者缺一不可． 如题中③⑤⑧不是等式，①不含未知数．
下列式子中_______________________是等式，______________________是方程．(填序号)①7x－6＝2； ②4－2＝2；③ x－6＝x2； ④a＋1；⑤9x2＋2y2－z2＝4；⑥ ＝7； ⑦x＝0；⑧x＋6＜9；⑨y≠3； ⑩π≈3.14.
下列各式是方程的是(　　)A．3x＋8 B．3＋5＝8C．a＋b＝b＋a D．x＋3＝7下列各式中不是方程的是(　　)A．2x＋3y＝1 B．－x＋y＝4C．x＝8 D．3π＋5≠7
如果方程中含有一个未知数(也称元)，并且所含未知数的项的次数是 1，那么我们就把这样的方程叫做一元一次方程.
一元一次方程的条件：(1)等号两边都是整式；(2)是方程；(3)只含一个未知数；(4)未知数的次数是1.
例2 下列方程中是一元一次方程的是(　　)A．x2－4x＋3＝0 B．3x－4y＝7C．3x＋2＝0 D. ＝9
A中未知数的最高次数为2；B中含有两个未知数；D中等号左边不是整式；C是一元一次方程.
识别一个方程是不是一元一次方程，必须注意这几点：(1)等号的两边都是整式；(2)所含未知数只有一个；(3)未知数的最高次数为1，(4)未知数的系数不为0.这四个条件缺一不可.
下列方程：①x－3＝ ；②0.5x＝1；③x－4x＝3；④ ＝5x＋2；⑤x＝6；⑥3y＋x＝0；⑦2x2－x＋2＝x2＋2x.其中是一元一次方程的有(　　)A．2个　　B．3个C．4个 D．5个
下列方程是一元一次方程的是(　　)A．x2－x＝4 B．2x－y＝0C．2x＝1 D. ＝2下列各式是一元一次方程的有(　　)① x＝ ；②3x－2；③ y－ ＝ －1；④1－7y2＝2y；⑤3(x－1)－3＝3x－6；⑥ ＋3＝2；⑦4(t－1)＝2(3t＋1)．A．1个 B．2个 C．3个 D．4个
能使方程两边相等的未知数的值，叫做方程的解.
例3 下列说法中正确的是(　　)A．y＝4是方程y＋4＝0的解B．x＝0.000 1是方程200x＝2的解C．t＝3是方程|t|－3＝0的解D．x＝1是方程 ＝－2x＋1的解
A.把y＝4代入方程左边得4＋4＝8，方程右边是0，故y＝4不是方程y＋4＝0的解；B.把x＝0.000 1代入方程左边得200×0.000 1＝0.02，方程右边是2，故x＝0.000 1不是方程200x＝2的解；C.把t＝3代入方程左边得|3|－3＝0，方程右边也是0，故t＝3是方程|t|－3＝0的解；D.把x＝1分别代入方程左、右两边，左边得 ，右边得－1，故x＝1不是方程 ＝－2x＋1的解.
检验方程的解的步骤：第一步：将数值分别代入原方程的左、右两边进行 计算；第二步：比较方程左、右两边的值；第三步：根据方程的解的意义下结论．
方程：①2x－3＝1；② x＝1；③ x－ ＝ ；④4(x－1)(x＋1)＝3中，解为x＝2的一元一次方程有(　　)A．1个　B．2个　C．3个　D．4个
写出一个一元一次方程，同时满足下列两个条件：①未知数的系数是2；②方程的解为3，则这个方程为_______________________．x＝3是下列哪个方程的解(　　)A．2x＋7＝11 B．5x－8＝2x＋1C．3x＝1 D．－x＝3
2x＋1＝7(答案不唯一)
例4 某市举行中学生足球比赛，规定平局时不再进行加时赛，并且胜一场得3分，平一场得1分，负一场得0分.实验中学足球队参加了 10场比赛，只负了1场，共得21分.该校足球队胜了几场？
该校足球队得分满足相等关系3×胜的场数+1×平的场数+0×负的场数=21，即 3×胜的场数+1×(10－1－胜的场数) =21.
设实验中学足球队胜了 x场，那么 3x+(9－x) = 21.解得 x=6.答：实验中学胜了 6场.
列实际问题中的一元一次方程的一般步骤：(1)弄清问题中的数量关系，运用建模思想将其转化 为数学问题；(2)设适当未知数；(3)找出能够表示问题中全部含义的一个主要相等关 系；(4)列一元一次方程．
一个物体现在的速度是7 m/s，其速度每秒增加2 m/s，则再经过多少秒，它的速度为19 m/s？(只列方程)
设再经过x s，它的速度为19 m/s，根据题意得7＋2x＝19.
【中考·南平】闽北某村原有林地120公顷，旱地60公顷，为适应产业结构调整，需把一部分旱地改造为林地，改造后，旱地面积占林地面积的20%，设把x公顷旱地改造为林地，则可列方程为(　　)A．60－x＝20%(120＋x)B．60＋x＝20%×120C．180－x＝20%(60＋x)D．60－x＝20%×120
【中考·绥化】一个长方形的周长为30 cm，若这个长方形的长减少1 cm，宽增加2 cm就可成为一个正方形，设长方形的长为x cm，可列方程为(　　)A．x＋1＝(30－x)－2 B．x＋1＝(15－x)－2C．x－1＝(30－x)＋2 D．x－1＝(15－x)＋2
1. 判断一个方程是不是一元一次方程要做到“两看”：一 看原方程必须具备：方程两边是整式，只含有一个未知 数；二看化简后的方程必须具备：未知数的次数为1， 系数不为0. 2. 代入检验法是检验方程解的一种有效的数学方法．它 的一般步骤为：(1)把未知数的值分别代入方程的左右 两边；(2)分别计算出左边的值和右边的值；(3)若左右 两边的值相等，即是方程的解，反之不是方程的解．上 述步骤可简化为：“一代二算三判”．