2021年内蒙古包头市中考数学一模试卷

这是一份2021年内蒙古包头市中考数学一模试卷，共34页。试卷主要包含了下列计算结果为正数的是，小明的作业本上有以下四题，下列命题正确的是等内容，欢迎下载使用。
2021年内蒙古包头市中考数学一模试卷
一．选择题：本大题共有12小题每小题0分，共36分。每小题只有一个正确选项请将答题卡上对应题目的答案标号涂黑。
1．下列计算结果为正数的是（　　）
A．﹣|﹣2| B．﹣（﹣1）0 C．（﹣1）﹣2 D．﹣32
2．某种福利彩票特等奖的中奖率为科学记数法表示为（　　）
A．5×10﹣7 B．5×10﹣6 C．2×10﹣7 D．2×10﹣6
3．如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示该位置上小正方体的个数，则该几何体的左视图是（　　）

A． B．
C． D．
4．若代数式有意义，则x的取值范围是（　　）
A．x≥0 B．x≠1 C．x≥0且x≠1 D．x＞1
5．小明的作业本上有以下四题：①﹣（a﹣1）＝1﹣a；②（a2）3﹣（﹣a3）2＝0；③a5+a5＝2a5；④（2a）3＝6a3，做错的题是（　　）
A．① B．② C．③ D．④
6．在安全教育知识党赛中，某校对学生成绩进行了抽样调查被抽取的7名学生的成绩如下（单位：分）：85，92，93，87，95，94，92，则这组数据的中位数和众数分别是（　　）
A．92，92 B．92，93 C．93，92 D．87，92
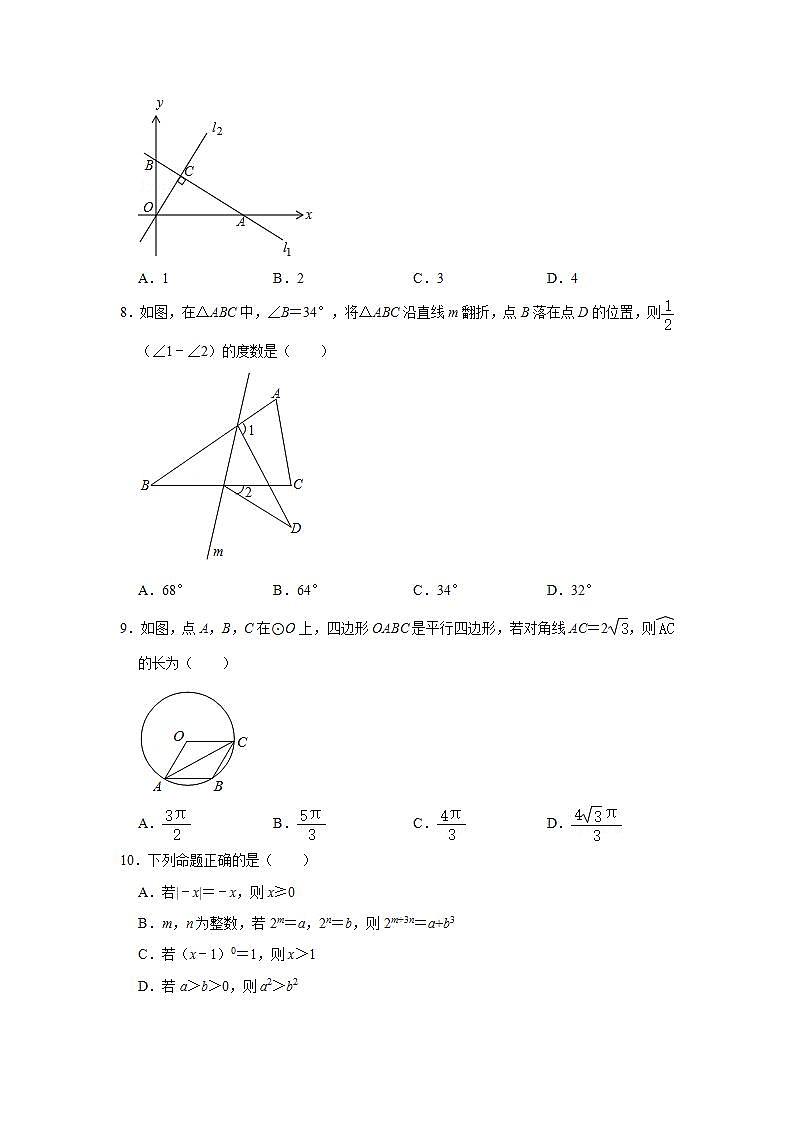
7．如图，在平面直角坐标系中，直线l1：y＝﹣x+5与x轴、y轴分别交于点A和点B，直线l2经过坐标原点，且l2⊥l1，垂足为C，则点C到y轴的距离为（　　）

A．1 B．2 C．3 D．4
8．如图，在△ABC中，∠B＝34°，将△ABC沿直线m翻折，点B落在点D的位置，则（∠1﹣∠2）的度数是（　　）

A．68° B．64° C．34° D．32°
9．如图，点A，B，C在⊙O上，四边形OABC是平行四边形，若对角线AC＝2，则的长为（　　）

A． B． C． D．
10．下列命题正确的是（　　）
A．若|﹣x|＝﹣x，则x≥0
B．m，n为整数，若2m＝a，2n＝b，则2m+3n＝a+b3
C．若（x﹣1）0＝1，则x＞1
D．若a＞b＞0，则a2＞b2
11．如图，ABCD的顶点A，C在反比例函数y＝的图象上，顶点B、D在反比例函数y＝的图象上，CD∥y轴，对角线AC，BD的交点恰好是坐标原点O．若▱ABCD＝24，k1＝﹣2k2，则k1的值为（　　）

A．﹣4 B．﹣6 C．﹣8 D．﹣10
12．如图，在正方形ABCD中，E是对角线BD上一点（BE＜DE），将线段CE绕点C按顺时针方向旋转90°得到线段CE′，连接AE′，DE‘，EE′．
下列结论：
①若∠BAE＝20°，则∠DE′E＝70°；
②BE2+DE2＝2AE2；
③若∠BAE＝30°，则DE＝BE；
④若BC＝9，EC＝10，则sin∠DEC＝．
其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
二、填空题：本大题共有8小题，每小题0分，共24分。请把答案填在答题卡上对应的横线上。
13．已知y＝x﹣3，则代数式x2﹣2xy+y2的值为 　 　．
14．若不等式组的解集是x＞3，则m的取值范围是 　 　．
15．六个学生进行投篮比赛，投进的个数分别为14，15，15，17，17，18，这六个数的平均数是 　 　．
16．化简：＝　 　．
17．如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，且AD＝，DE∥BC，∠DBE＝90°，连接AE．若AC＝3，BC＝4，则AE的长为 　 　．

18．如图，在等边三角形ABC中，点D，E分别在边AB，AC上，把△ABC沿着DE翻折，使点A恰好落在边BC上的点P处．若△BDP的周长为4，△CPE的周长为5，则的值为 　 　．

19．如图，在菱形ABCD中，∠ABC＝30°，AD＝6，点P，M分别是边AB和对角线BD上的动点，则AM+PM的最小值为 　 　．

20．在平面直角坐标系中，点A和点B的坐标分别为（0，2）和（4，2），若抛物线y＝ax2﹣2ax+3（a＜0）与线段AB有且只有一个交点，则a的取值范围是 　 　．
三、解答题：本大题共有6小题，共60分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置
21．如图，一个可以自由转动的质地均匀的转盘，被分成三个面积相等的扇形，每个扇形分别标有数字﹣3，1，2．转动转盘两次，待转盘自动停止后，指针指向扇形内的数字分别作为关于x的一元二次方程ax2+2x+c＝0中的a，c的值（若指针指向两个扇形的交线，则不计该次转动，重新转动转盘，直到指针指向一个扇形的内部为止）．其中第一次转动转盘后指针指向扇形内的数字记为a，第二次转动转盘后指针指向扇形内的数字记为c．
（1）请用列表或画树状图的方法写出（a，c）所有可能出现的结果；
（2）求出关于x的一元二次方程ax2+2x+c＝0有两个实数根的概率．

22．如图，数学实践活动小组想测量塔CD的高度．一测量人员在A处仰望塔顶，测得仰角为30°，再往塔的方向前进60米至B处，测得仰角为75°（测量人员身高不计）．
（1）求塔CD的高度．
（2）求测量人员在B处时，他到塔CD的距离．

23．某水果店销售一种水果，经市场调查发现，这种水果的日销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示．这种水果的进价为a（元/千克），日销售利润为w（元），当销售单价为14元，日销售利润为384元．
（1）求y关于x的函数关系式及a的值；
（2）当这种水果的销售单价是多少时，日销售获得的利润最大？
（3）若该水果店一次性购进这种水果50千克，这种水果的保质期为10天，按照（2）中获得最大利润的方式进行销售，能否销售完这批水果？请说明理由．

24．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作MN⊥AC，垂足为M，交AB的延长线于点N，过点B作BG⊥MN，垂足为G，连接CM．
（1）求证：直线MN是⊙O的切线；
（2）求证：BD2＝AC•BG；
（3）若BN＝OB，⊙O的半径为1，求tan∠ANC的值．

25．如图，在矩形ABCD中，AB＝4，BC＝6，E是AD上一点，且AE＝2，M是AB上一动点N是射线BC上一动点，连接ME并延长交CD的延长线于点F，连接EN，当∠MEN＝90°时，连接NF．
（1）如图1，当点N在点C的左侧时，连接MN，NF与AD相交于点H，点K在EF上，连接HK．
①若NC＝2，求AM的长．
②在①的条件下，若KF＝，求证：KH∥MN；
（2）如图2，当点N在点C的右侧时，过点E作EG⊥NF，垂足为G．若CN＝1，求MF+EG的值．

26．如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴交于A（﹣2，0），B（3，0）两点，与y轴交于点C，连接AC，BC．
（1）求此抛物线的解析式及对称轴；
（2）D是抛物线的对称轴上一点，且位于x轴的下方若S△ACD＝6，求点D的坐标；
（3）取点E（0，2），连接AE，在第四象限内的抛物线上是否存在一点F，使得∠BCF＝∠CAE？若存在，求出点F的坐标；若不存在，请说明理由．


2021年内蒙古包头市中考数学一模试卷
参考答案与试题解析
一．选择题：本大题共有12小题每小题0分，共36分。每小题只有一个正确选项请将答题卡上对应题目的答案标号涂黑。
1．下列计算结果为正数的是（　　）
A．﹣|﹣2| B．﹣（﹣1）0 C．（﹣1）﹣2 D．﹣32
【分析】根据绝对值的意义，有理数的乘方，零指数幂，负整数指数幂的运算法则进行计算，从而作出判断．
【解答】解：A、﹣|﹣2|＝﹣2＜0，结果为负数，故此选项不符合题意；
B、﹣（﹣1）0＝﹣1＜0，结果为负数，故此选项不符合题意；
C、（﹣1）﹣2＝1＞0，结果为正数，故此选项符合题意；
D、﹣32＝﹣9＜0，结果为负数，故此选项不符合题意；
故选：C．
2．某种福利彩票特等奖的中奖率为科学记数法表示为（　　）
A．5×10﹣7 B．5×10﹣6 C．2×10﹣7 D．2×10﹣6
【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．
【解答】解：＝0.0000002＝2×10﹣7．
故选：C．
3．如图是由几个大小相同的小正方体搭成的几何体的俯视图，小正方形中的数字表示该位置上小正方体的个数，则该几何体的左视图是（　　）

A． B．
C． D．
【分析】根据俯视图中每列正方形的个数，再画出从正面，左面看得到的图形即可．
【解答】解：从该几何体的俯视图中得到：该几何体有两层，两列组成，
该几何体的左视图是：
．
故选：D．
4．若代数式有意义，则x的取值范围是（　　）
A．x≥0 B．x≠1 C．x≥0且x≠1 D．x＞1
【分析】根据二次根式和分式有意义的条件列出不等式组求解．
【解答】解：由题意可得，
解得：x≥0且x≠1，
故选：C．
5．小明的作业本上有以下四题：①﹣（a﹣1）＝1﹣a；②（a2）3﹣（﹣a3）2＝0；③a5+a5＝2a5；④（2a）3＝6a3，做错的题是（　　）
A．① B．② C．③ D．④
【分析】根据去括号法则判断①；根据幂的乘方法则判断②；根据合并同类项法则判断③；根据积的乘方法则判断④．
【解答】解：①﹣（a﹣1）＝1﹣a，正确；②（a2）3﹣（﹣a3）2＝0，正确；③a5+a5＝2a5，正确；④（2a）3＝8a3，错误；
故选：D．
6．在安全教育知识党赛中，某校对学生成绩进行了抽样调查被抽取的7名学生的成绩如下（单位：分）：85，92，93，87，95，94，92，则这组数据的中位数和众数分别是（　　）
A．92，92 B．92，93 C．93，92 D．87，92
【分析】先把数据从小到大（或从大到小）排列，再得出中位数和众数即可．
【解答】解：数据从小到大排列为：85，87，92，92，93，94，95，97，
所以这组数据的中位数是92，众数是92，
故选：A．
7．如图，在平面直角坐标系中，直线l1：y＝﹣x+5与x轴、y轴分别交于点A和点B，直线l2经过坐标原点，且l2⊥l1，垂足为C，则点C到y轴的距离为（　　）

A．1 B．2 C．3 D．4
【分析】过点C作CD⊥y轴于点D，由直线AB的解析式求出点A和点B的坐标，得到OA和OB的长度，利用勾股定理求出AB的长度，再结合等面积法求出OC的长度，然后继续利用勾股定理求BC，最后再次利用等面积法求CD．
【解答】解：对直线y＝﹣x+5，当x＝0时，y＝5，当y＝0时，x＝10，
∴A（10，0），B（0，5），
∴OA＝10，OB＝5，
∴AB＝5，
∵S△ABO＝OA•OB＝OC•AB，
∴×10×5＝×5×OC，
∴OC＝2，
∴BC＝＝，
过点C作CD⊥x轴于点D，
∵S△CBO＝CD•OB＝OC•BC，
∴×2×＝×5×CD，
∴CD＝2，即点C到y轴的距离为2．
故选：B．

8．如图，在△ABC中，∠B＝34°，将△ABC沿直线m翻折，点B落在点D的位置，则（∠1﹣∠2）的度数是（　　）

A．68° B．64° C．34° D．32°
【分析】由折叠的性质可得到∠B与∠D的关系，再利用外角与内角的关系求出（∠1﹣∠2）的度数．
【解答】解：∵△EFD是由△EFB沿m翻折后的图形，
∴∠D＝∠B＝34°．
∵∠1＝∠B+∠3，∠3＝∠2+∠D，
∴∠1＝∠B+∠2+∠D＝68°+∠2．
∴∠1﹣∠2＝68°．
∴（∠1﹣∠2）＝34°．
故选：C．

9．如图，点A，B，C在⊙O上，四边形OABC是平行四边形，若对角线AC＝2，则的长为（　　）

A． B． C． D．
【分析】根据平行四边形的性质和OC＝OA得出四边形OABC是菱形，再根据垂径定理和三角函数求出圆心角和半径，即可求出答案．
【解答】解：连接OB，交AC于D，

∵四边形OABC是平行四边形，OC＝OA，
∴四边形OABC是菱形，OB⊥AC，
∵OA＝OB＝BC，
∴△OAB是等边三角形，∠AOB＝60°，
在Rt△OAD中，AD＝AC＝，
∴OA＝＝2，
∴的长是＝．
故选：C．
10．下列命题正确的是（　　）
A．若|﹣x|＝﹣x，则x≥0
B．m，n为整数，若2m＝a，2n＝b，则2m+3n＝a+b3
C．若（x﹣1）0＝1，则x＞1
D．若a＞b＞0，则a2＞b2
【分析】利用绝对值的意义对A进行判断；根据同底数幂的乘法法则和幂的乘方对B进行判断；根据零指数幂的意义对C进行判断；根据乘方的意义对D进行判断．
【解答】解：A．若|﹣x|＝﹣x，则x≤0，所以A选项不符合题意；
B．m，n为整数，若2m＝a，2n＝b，则2m+3n＝2m•23n＝2m•（2n）3＝ab3，所以B选项不符合题意；
C．若（x﹣1）0＝1，则x≠1，所以C选项不符合题意；
D．若a＞b＞0，则a2＞b2，所以D选项不符合题意．
故选：D．
11．如图，ABCD的顶点A，C在反比例函数y＝的图象上，顶点B、D在反比例函数y＝的图象上，CD∥y轴，对角线AC，BD的交点恰好是坐标原点O．若▱ABCD＝24，k1＝﹣2k2，则k1的值为（　　）

A．﹣4 B．﹣6 C．﹣8 D．﹣10
【分析】根据反比例函数的中心对称性对称四边形ABCD是平行四边形，从而得出S△COD＝S四边形ABCD＝6，然后根据反比例函数系数k的几何意义得到S△COD＝（|k1|+|k2|）＝6，由k1＝﹣2k2，即可求得k1＝﹣8．
【解答】解：由题意可知OA＝OC，OB＝OD，
∴四边形ABCD是平行四边形，
∴S△COD＝S四边形ABCD＝6，
∵CD∥y轴，
∴S△COD＝（|k1|+|k2|）＝6，
∵k1＝﹣2k2，
∴3|k2|＝12，
∵k2＞0，
∴k2＝4，
∴k2＝﹣2×4＝﹣8，
故选：C．
12．如图，在正方形ABCD中，E是对角线BD上一点（BE＜DE），将线段CE绕点C按顺时针方向旋转90°得到线段CE′，连接AE′，DE‘，EE′．
下列结论：
①若∠BAE＝20°，则∠DE′E＝70°；
②BE2+DE2＝2AE2；
③若∠BAE＝30°，则DE＝BE；
④若BC＝9，EC＝10，则sin∠DEC＝．
其中正确的结论有（　　）

A．4个 B．3个 C．2个 D．1个
【分析】首先通过SAS证明△BCE≌△DCE'，可证△DEE'是直角三角形，从而∠DEE'＝∠BCE＝∠BAE，故①正确；在Rt△E'CE中，E'E2＝CE'2+CE2＝2CE2，由正方形的对称性可知AE＝CE，故②正确；若∠BAE＝30°，则∠DEE'＝∠BCE＝∠BAE＝30°，在Rt△E'DE中，DE＝DE'，可知③错误；过点C作CM⊥BD，交BD于点M，在Rt△CME中，sin∠DEC＝，故④正确．
【解答】解：∵四边形ABCD是正方形，
∴BC＝CD，∠BCD＝90°，
∵线段CE绕点C按顺时针方向旋转90°得到线段CE′，
∴CE＝CE'，∠ECE'＝90°，
∴△ECE'是等腰直角三角形，
∴∠EE'C﹣∠E'EC＝45°，
∴∠BCD﹣∠ECD＝∠ECE'﹣∠ECD，
∴∠BCE＝∠DCE'，
在△BCE与△DCE'中，
，
∴△BCE≌△DCE'（SAS），
∴∠CDE'＝∠EBC＝45°，DE'＝BE，
∴∠EDE'＝∠EDC+∠CDE'＝45°+45°＝90°，
∴△DEE'是直角三角形，
∵四边形ABCD是正方形，E在对角线BD上，
∴∠BCE＝∠BAE，
∵∠DEC＝∠DEE'+∠E'EC＝∠EBC+∠BCE，∠E'EC＝∠EBC＝45°，
∴∠DEE'＝∠BCE＝∠BAE，
①∵∠BAE＝20°，
∴∠DE'E＝90°﹣∠DEE'＝70°，
故①正确；
②在Rt△E'DE中，
E'E2＝E'D2+DE2＝BE2+DE2，
在Rt△E'CE中，
E'E2＝CE'2+CE2＝2CE2，
∵四边形ABCD是正方形，E在对角线BD上，
∴AE＝CE，
∴E'E2＝2CE'2＝2AE2，
∴BE2+DE2＝2AE2，
故②正确；
③若∠BAE＝30°，则∠DEE'＝∠BCE＝∠BAE＝30°，
在Rt△E'DE中，DE＝DE'，
∵BE＝DE'，
∴DE＝BE，
故③错误；
④如图，过点C作CM⊥BD，交BD于点M，

∵四边形ABCD是正方形，BC＝9，
∴CM＝9，
在Rt△CME中，sin∠DEC＝，
故④正确，
故选：B．
二、填空题：本大题共有8小题，每小题0分，共24分。请把答案填在答题卡上对应的横线上。
13．已知y＝x﹣3，则代数式x2﹣2xy+y2的值为 　9　．
【分析】求出x﹣y＝3，根据完全平方公式得出x2﹣2xy+y2＝（x﹣y）2，再代入求出答案即可．
【解答】解：∵y＝x﹣3，
∴x﹣y＝3，
∴x2﹣2xy+y2
＝（x﹣y）2
＝32
＝9，
故答案为：9．
14．若不等式组的解集是x＞3，则m的取值范围是 　m≤3　．
【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小找不到确定不等式组的解集．
【解答】解：解不等式x+5＜3x﹣1，得：x＞3，
∵x＞m且不等式组的解集为x＞3，
∴m≤3，
故答案为m≤3．
15．六个学生进行投篮比赛，投进的个数分别为14，15，15，17，17，18，这六个数的平均数是 　16　．
【分析】先根据平均数的定义列出算式，再求出平均数即可．
【解答】解：平均数为×（14+15+15+17+17+18）＝16，
故答案为：16．
16．化简：＝　﹣　．
【分析】根据分式的减法和除法可以解答本题．
【解答】解：
＝（﹣）•
＝•
＝•
＝﹣，
故答案为：﹣．
17．如图，在Rt△ABC中，∠ACB＝90°，D是AB上一点，且AD＝，DE∥BC，∠DBE＝90°，连接AE．若AC＝3，BC＝4，则AE的长为 　　．

【分析】根据勾股定理得到AB＝＝＝5，根据相似三角形的性质得到BE＝2，根据勾股定理即可得到AE＝．
【解答】解：∵∠ACB＝90°，AC＝3，BC＝4，
∴AB＝＝＝5，
∵AD＝，
∴BD＝AB﹣AD＝，
∵DE∥BC，
∴∠ABC＝∠BDE，
∵∠C＝∠DBE＝90°，
∴△ACB∽△EBD，
∴＝，
∴＝，
∴BE＝2，
∴AE＝＝＝，
故答案为：．
18．如图，在等边三角形ABC中，点D，E分别在边AB，AC上，把△ABC沿着DE翻折，使点A恰好落在边BC上的点P处．若△BDP的周长为4，△CPE的周长为5，则的值为 　　．

【分析】由折叠的性质可得AD＝DP，AE＝PE，∠A＝∠DPE＝60°，通过证明△BDP∽△CPE，由相似三角形的性质可求解．
【解答】解：∵△ABC是等边三角形，
∴∠B＝∠C＝∠A＝60°，
∵把△ABC沿着DE翻折，
∴△ADE≌△PDE，
∴AD＝DP，AE＝PE，∠A＝∠DPE＝60°，
∵∠DPC＝∠B+∠BDP＝∠DPE+∠EPC，
∴∠BDP＝∠EPC，
∴△BDP∽△CPE，
∴＝，
∴＝，
故答案为：．
19．如图，在菱形ABCD中，∠ABC＝30°，AD＝6，点P，M分别是边AB和对角线BD上的动点，则AM+PM的最小值为 　3　．

【分析】连接CM，先说明△ABM≌△CBM（SAS），得AM＝CM，即AM+PM的最小值就是CM+PM的最小值，当P、M、C三点共垂线时，AM+PM的最小，即可求解．
【解答】解：连接CM，
∵四边形ABCD是菱形，
∴BD平分∠ABC，AB＝CB，
∴ABM＝∠CBM，
∵BM＝BM，
∴△ABM≌△CBM（SAS），
∴AM＝CM，
∴AM+PM的最小值就是CM+PM的最小值，
当P、M、C三点共垂线时，AM+PM的最小，
在Rt△BPC中，∠ABC＝30°，
∴PC＝＝6＝3．
故答案为：3．

20．在平面直角坐标系中，点A和点B的坐标分别为（0，2）和（4，2），若抛物线y＝ax2﹣2ax+3（a＜0）与线段AB有且只有一个交点，则a的取值范围是 　a≤﹣　．
【分析】根据抛物线的对称轴公式：x＝﹣计算抛物线的对称轴为：直线x＝1，得抛物线y＝ax2﹣2ax+3与y轴交于点（0，3），先计算过边界点B时，a＝﹣，对于抛物线y＝ax2﹣2ax+3，当a＜0时，无论a取何值，抛物线的对称轴不变，抛物线与y轴的交点（0，3）都在点A（0，2）的上方，随着|a|的值变大，抛物线的开口越小，可得答案．
【解答】解：抛物线y＝ax2﹣2ax+3的对称轴为直线：x＝﹣＝1，
对于y＝ax2﹣2ax+3，
当x＝0时，y＝3，
∴抛物线y＝ax2﹣2ax+3与y轴交于点（0，3），
∵a＜0，
∴抛物线的开口向下，
∴抛物线y＝ax2﹣2ax+3在平面直角坐标系中的大致位置如图：

当抛物线y＝ax2﹣2ax+3经过点B（4，2）时，2＝a×42﹣2a×4+3，
解得a＝﹣，
对于抛物线y＝ax2﹣2ax+3，当a＜0时，无论a取何值，抛物线的对称轴不变，抛物线与y轴的交点（0，3）都在点A（0，2）的上方，随着|a|的值变大，抛物线的开口越小，
∵抛物线y＝ax2﹣2ax+3与线段AB只有一个交点，
∴|a|≥|﹣|，
又∵a＜0，
∴a≤﹣（两个负数比较大小，绝对值较大的反而小）．
∴a的取值范围是a≤﹣．
故答案为：a≤﹣．
三、解答题：本大题共有6小题，共60分。请将必要的文字说明、计算过程或推理过程写在答题卡的对应位置
21．如图，一个可以自由转动的质地均匀的转盘，被分成三个面积相等的扇形，每个扇形分别标有数字﹣3，1，2．转动转盘两次，待转盘自动停止后，指针指向扇形内的数字分别作为关于x的一元二次方程ax2+2x+c＝0中的a，c的值（若指针指向两个扇形的交线，则不计该次转动，重新转动转盘，直到指针指向一个扇形的内部为止）．其中第一次转动转盘后指针指向扇形内的数字记为a，第二次转动转盘后指针指向扇形内的数字记为c．
（1）请用列表或画树状图的方法写出（a，c）所有可能出现的结果；
（2）求出关于x的一元二次方程ax2+2x+c＝0有两个实数根的概率．

【分析】（1）画树状图，即可求解；
（2）共有9种等可能的结果，使关于x的一元二次方程ax2+2x+c＝0有两个实数根的结果有5种，再由概率公式求解即可．
【解答】解：（1）画树状图如下：

共有9种等可能的结果，分别为（﹣3，﹣3），（﹣3，1），（﹣3，2），（1，﹣3），（1，1），（1，2），（2，﹣3），（2，1），（2，2）；
（2）由（1）得：共有9种等可能的结果，使关于x的一元二次方程ax2+2x+c＝0有两个实数根的结果有5种，
∴关于x的一元二次方程ax2+2x+c＝0有两个实数根的概率为．
22．如图，数学实践活动小组想测量塔CD的高度．一测量人员在A处仰望塔顶，测得仰角为30°，再往塔的方向前进60米至B处，测得仰角为75°（测量人员身高不计）．
（1）求塔CD的高度．
（2）求测量人员在B处时，他到塔CD的距离．

【分析】（1）过点B作BE⊥AC于E，由含30°角的直角三角形的性质得BE＝AB＝30（米），则AE＝BE＝30（米），再证CE＝BE＝30米，则AC＝AE+CE＝（30+30）米，然后由含30°角的直角三角形的性质即可求解；
（2）由含30°角的直角三角形的性质AD＝CD＝（45+15）米，即可求解．
【解答】解：（1）过点B作BE⊥AC于E，如图所示：
则∠AEB＝∠CEB＝90°，
∵∠A＝30°，AB＝60米，
∴BE＝AB＝30（米），
∴AE＝BE＝30（米），
∵∠DBC＝∠A+∠BCE＝75°，
∴∠BCE＝75°﹣30°＝45°，
∴△BCE是等腰直角三角形，
∴CE＝BE＝30米，
∴AC＝AE+CE＝（30+30）米，
又∵∠ADC＝90°，∠A＝30°，
∴CD＝AC＝（15+15）米，
答：塔CD的高度为（15+15）米；
（2）∵∠ADC＝90°，∠A＝30°，
∴AD＝CD＝（45+15）米，
∴BD＝AD﹣AB＝（15﹣15）米，
答：测量人员在B处时，他到塔CD的距离为（15﹣15）米．

23．某水果店销售一种水果，经市场调查发现，这种水果的日销售量y（千克）与销售单价x（元/千克）之间的函数关系如图所示．这种水果的进价为a（元/千克），日销售利润为w（元），当销售单价为14元，日销售利润为384元．
（1）求y关于x的函数关系式及a的值；
（2）当这种水果的销售单价是多少时，日销售获得的利润最大？
（3）若该水果店一次性购进这种水果50千克，这种水果的保质期为10天，按照（2）中获得最大利润的方式进行销售，能否销售完这批水果？请说明理由．

【分析】（1）利用待定系数法求解可得，根据“日销售利润＝单件利润×日销售量”列出方程求出a即可求解；
（2）根据“日销售利润＝单件利润×日销售量”列出函数解析式，并配方成顶点式即可得出最大值；
（3）求出在（2）中情况下，求出日销售量56千克，据此求得10天的总销售量，比较即可得出．
【解答】解：（1）设y关于x的函数关系式为y＝kx+b（k≠0），
将（10，80）和（14，48）代入，
得：，
解得：，
∴y关于x的函数关系式为y＝﹣8x+160，
由图可得，（14﹣a）×48＝384，
解得：a＝6，
∴a的值为6；
（2）由题意，得：w＝（x﹣6）（﹣8x+160）＝﹣8（x﹣13）2+392，
∵﹣8＜0，
∴当x＝13时，w有最大值，最大值为392，
∴这种水果的销售单价是13元时，日销售获得的利润最大；
（3）能，理由：
∵按照（2）中获得最大利润的方式进行销售，
由（1）得日销量y＝﹣8×13+160＝56（千克），
∴56＞50，
∴该水果店能销售完这批水果．
24．如图，在△ABC中，AB＝AC，以AB为直径的⊙O交BC于点D，过点D作MN⊥AC，垂足为M，交AB的延长线于点N，过点B作BG⊥MN，垂足为G，连接CM．
（1）求证：直线MN是⊙O的切线；
（2）求证：BD2＝AC•BG；
（3）若BN＝OB，⊙O的半径为1，求tan∠ANC的值．

【分析】（1）由AB是直径得AD⊥BC，又AB＝AC得∠BAD＝∠CAD，由OA＝OD得∠ODA＝∠BAD，进而可推出∠ODM＝90°；
（2）由条件推出BD＝CD，CM＝BG，由△CDM∽△CAD，进一步可得结论；
（3）由条件推得∠BOD＝60°，进而∠ABC＝60°，可得△ABC是等边三角形，从而CO⊥AB，进一步可求得结果．
【解答】证：（1）如图1，

连接AD，OD，
∵AB是⊙O的直径，
∴∠ADB＝∠ACD＝90°，
即AD⊥BC，
∵AB＝AC，
∴∠BAD＝∠CAD，BD＝CD，
∵OA＝OD，
∴∠ODA＝∠BAD，
∴∠OAD＝∠CAD，
∵NM⊥AC，
∴∠AMN＝90°，
∴∠DAC+∠ADM＝90°，
∴∠ODA+∠ADM＝90°，
即∠ODM＝90°，
∴OD⊥MN，
∴直线MN是⊙O的切线；
（2）由（1）知，
∠ADC＝90°，BD＝CD，
∴∠ADC＝∠DMC＝90°，
∵∠ACD＝∠DCM，
∴△CMD∽△CDA，
∴＝，
∴CD2＝AC•CM，
∴BD2＝AC•CM，
在△BGD和△MCD中，
，
∴△BGD≌△CDM（AAS），
∴BG＝CM，
∴BD2＝AC•BG；
（3）如图2，

连接OD，OC，
由（1）∠ODN＝90°，
∵OD＝OB＝BN＝1，
∴cos∠DON＝＝，
∴∠DON＝60°，
∵AB＝AC，
∴△ABC是等边三角形，
∵OA＝OB，
∴CO⊥AB，OC＝AC•cos60°＝，
∴tan∠ANC＝＝．
25．如图，在矩形ABCD中，AB＝4，BC＝6，E是AD上一点，且AE＝2，M是AB上一动点N是射线BC上一动点，连接ME并延长交CD的延长线于点F，连接EN，当∠MEN＝90°时，连接NF．
（1）如图1，当点N在点C的左侧时，连接MN，NF与AD相交于点H，点K在EF上，连接HK．
①若NC＝2，求AM的长．
②在①的条件下，若KF＝，求证：KH∥MN；
（2）如图2，当点N在点C的右侧时，过点E作EG⊥NF，垂足为G．若CN＝1，求MF+EG的值．

【分析】（1）①过点N作NP⊥AD于点P，可得∠NPE＝∠NPD＝90°，利用矩形性质和判定可证四边形PNCD是矩形，进而可证△EAM∽△NPE，求得AM＝1；
②由AB∥CF，可得△AEM∽△DEF，求得DF＝2，FC＝6，由DH∥CN，可证△FHD∽△FNC，可得＝＝，再运用勾股定理求得：EF＝2，EM＝，MF＝3，FK＝，进而可得＝，可证得△FKH∽△FMN，得出∠FKH＝∠FMN即可；
（2）如图2，过点N作NR⊥AD，交AD的延长线于点R，由RN＝DC＝4，CN＝1，DE＝4，可得DR＝CN＝1，ER＝5，运用勾股定理得EN＝，可证△AME∽△REN，得出ME＝，再由△AME∽△DFE，可得FE＝，FE＝EN，再利用三角函数定义即可求得答案．
【解答】解：（1）如图1，
①过点N作NP⊥AD于点P，
∴∠NPE＝∠NPD＝90°，
∵四边形ABCD是矩形，
∴∠ADC＝∠BCD＝90°，CD＝AB＝4，AD＝BC＝6，
∵∠PDC＝∠NCD＝∠DPN＝90°，
∴四边形PNCD是矩形，
∴NP＝CD＝4，
∵NC＝2，
∴DP＝2，
∵AE＝2，
∴EP＝AD﹣AE﹣DP＝6﹣2﹣2＝2，
∵∠MEN＝90°
∴∠AEM+∠PEN＝90°，
∵∠PNE+∠PEN＝90°，
∴∠AEM＝∠PNE，
∵∠EAM＝∠NPE＝90°，
∴△EAM∽△NPE，
∴＝，
∴AM＝＝＝1．
②证明：∵AB∥CF，
∴∠AME＝∠DFE，
∵∠AEM＝∠DEF，
∴△AEM∽△DEF，
∴＝，
∵AE＝2，DE＝4，AM＝1，
∴DF＝＝＝2，
∴FC＝CD+FD＝6，
∵DH∥CN，
∴∠FHD＝∠FNC，∠HFD＝∠NFC，
∴△FHD∽△FNC，
∴＝＝，
在Rt△EDF中，EF＝＝＝2，
在Rt△EAM中，EM＝＝＝，
∴MF＝EM+EF＝+2＝3，
∵FK＝，
∴＝＝，
∴＝，
∵∠KFH＝∠MFN，
∴△FKH∽△FMN，
∴∠FKH＝∠FMN，
∴KH∥MN．
（2）如图2，过点N作NR⊥AD，交AD的延长线于点R，
则∠R＝∠NCD＝∠CDR＝90°，
∴四边形CDRN是矩形，
∴RN＝DC＝4，
∵CN＝1，DE＝4，
∴DR＝CN＝1，
∴ER＝ED+DR＝5，
在Rt△ERN中，EN＝＝＝，
∵∠AEM+∠REN＝90°，∠AME+∠AEM＝90°，
∴∠AME＝∠REN，
∵∠MAE＝∠∠ERN＝90°，
∴△AME∽△REN，
∴＝，
∴ME＝＝＝，
∵△AME∽△DFE，
∴＝，
∴FE＝＝＝，
∴FE＝EN，
∵∠NEF＝90°，
∴∠EFG＝45°，
在Rt△EGF中，EG＝EF•sin45°＝，
∵MF+ME+EF＝，
∴MF+EG＝+×＝2．


26．如图，在平面直角坐标系中，抛物线y＝ax2+bx+3（a≠0）与x轴交于A（﹣2，0），B（3，0）两点，与y轴交于点C，连接AC，BC．
（1）求此抛物线的解析式及对称轴；
（2）D是抛物线的对称轴上一点，且位于x轴的下方若S△ACD＝6，求点D的坐标；
（3）取点E（0，2），连接AE，在第四象限内的抛物线上是否存在一点F，使得∠BCF＝∠CAE？若存在，求出点F的坐标；若不存在，请说明理由．

【分析】（1）将A（﹣2，0），B（3，0）代入y＝ax2+bx+3，用待定系数法可得抛物线的解析式为y＝﹣x2+x+3，即得对称轴为直线x＝；
（2）过D作DE∥AC交x轴于E，连接CE，由y＝﹣x2+x+3得C（0，3），设直线AC为y＝kx+3，将A（﹣2，0）代入可求出直线AC为y＝x+3，设D（，m），m＜0，可得直线DE为y＝x+m﹣，即得E（﹣m，0），AE＝﹣m，故S△ACE＝AE•OC＝﹣m，而DE∥AC，S△ACD＝6，可得﹣m＝6，即得D（，﹣）；
（3）作A关于y轴的对称点G，作直线CG交抛物线于F，由A（﹣2，0），E（0，2），可得∠CAE＝45°﹣∠ACE，由B（3，0），C（0，3），得∠BCF＝45°﹣∠GCO，根据A、G关于y轴对称，知∠ACE＝∠GCO，G（2，0），故∠BCF＝∠CAE，即F是满足条件的点，设直线CG为y＝tx+3，将G（2，0）代入得直线CG为y＝﹣x+3，解得F（4，﹣3）．
【解答】解：（1）将A（﹣2，0），B（3，0）代入y＝ax2+bx+3得：
，解得，
∴抛物线的解析式为y＝﹣x2+x+3，
而﹣＝﹣＝，
∴对称轴为直线x＝；
（2）过D作DE∥AC交x轴于E，连接CE，如图：，

由y＝﹣x2+x+3得C（0，3），
设直线AC为y＝kx+3，将A（﹣2，0）代入得：0＝﹣2k+3，
∴k＝，
∴直线AC为y＝x+3，
设D（，m），m＜0，
由DE∥AC可设直线DE为y＝x+b，
将D（，m）代入得：m＝+b，
∴b＝m﹣，
∴直线DE为y＝x+m﹣，
在y＝x+m﹣中，令y＝0得x+m﹣＝0，
∴x＝﹣m，
∴E（﹣m，0），
∴AE＝（﹣m）﹣（﹣2）＝﹣m，
∴S△ACE＝AE•OC＝×（﹣m）×3＝﹣m，
∵DE∥AC，
∴S△ACD＝S△ACE，
∵S△ACD＝6，
∴﹣m＝6，
∴m＝﹣，
∴D（，﹣）；
（3）存在一点F，使得∠BCF＝∠CAE，理由如下：
作A关于y轴的对称点G，作直线CG交抛物线于F，如图：

∵A（﹣2，0），E（0，2），
∴△AOE是等腰直角三角形，
∴∠AEO＝45°，
∴∠CAE＝∠AEO﹣∠ACE＝45°﹣∠ACE，
∵B（3，0），C（0，3），
∴∠BCO＝45°，
∴∠BCF＝∠BCO﹣∠GCO＝45°﹣∠GCO，
∵A、G关于y轴对称，
∴∠ACE＝∠GCO，G（2，0），
∴∠BCF＝∠CAE，即F是满足条件的点，
设直线CG为y＝tx+3，将G（2，0）代入得0＝2t+3，
∴t＝﹣，
∴直线CG为y＝﹣x+3，
解得或，
∴F（4，﹣3）．