2020-2021学年2.1古典概型的特征和概率计算公式教案及反思
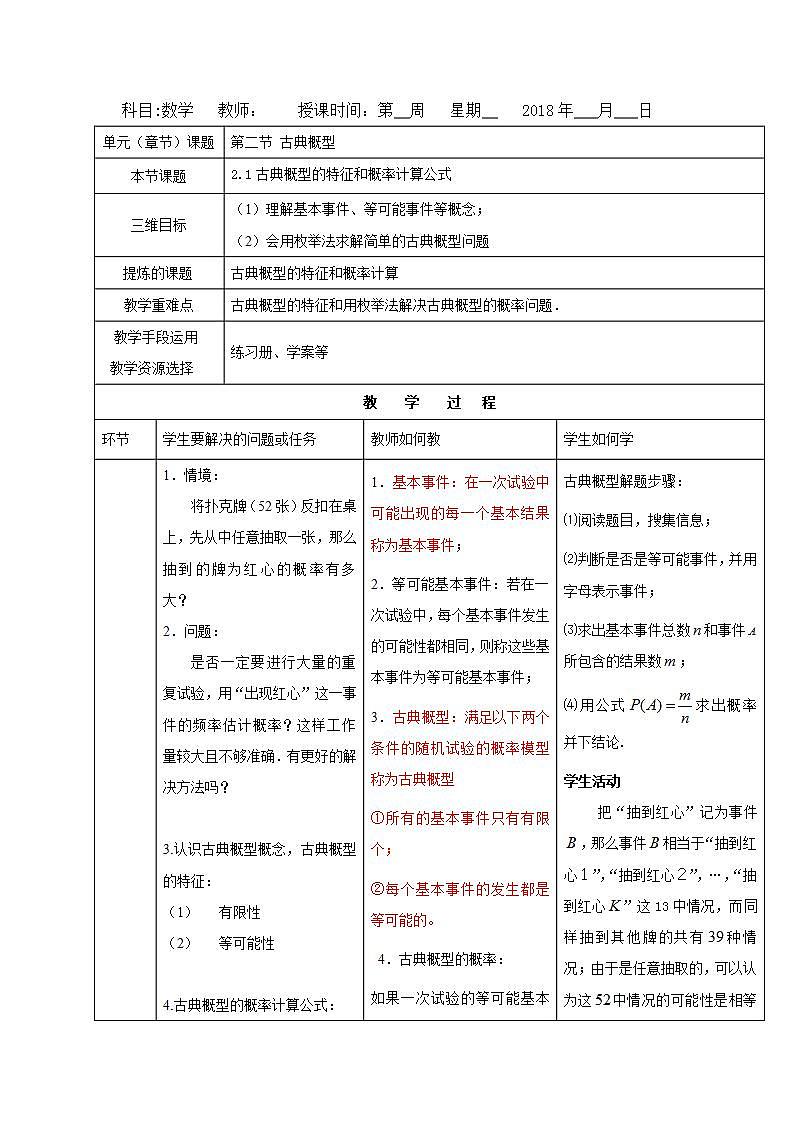
展开科目:数学 教师: 授课时间:第 周 星期 2018年 月 日
单元(章节)课题 | 第二节 古典概型 | |||
本节课题 | 2.1古典概型的特征和概率计算公式 | |||
三维目标 | (1)理解基本事件、等可能事件等概念; (2)会用枚举法求解简单的古典概型问题 | |||
提炼的课题 ] | 古典概型的特征和概率计算 | |||
教学重难点 | 古典概型的特征和用枚举法解决古典概型的概率问题. | |||
教学手段运用 学 ] 教学资源选择 . .X.X. ] | 练习册、学案等 | |||
教 学 过 程 | ||||
环节 | 学生要解决的问题或任务 | 教师如何教 | 学生如何学 | |
| 1.情境: 将扑克牌(52张)反扣在桌上,先从中任意抽取一张,那么抽到的牌为红心的概率有多大? 2.问题: 是否一定要进行大量的重复试验,用“出现红心”这一事件的频率估计概率?这样工作量较大且不够准确.有更好的解决方法吗?
3.认识古典概型概念,古典概型的特征: (1) 有限性 (2) 等可能性
4.古典概型的概率计算公式:
5.古典概型概率计算的应用。
| 1.基本事件:在一次试验中可能出现的每一个基本结果称为基本事件; 2.等可能基本事件:若在一次试验中,每个基本事件发生的可能性都相同,则称这些基本事件为等可能基本事件; 3.古典概型:满足以下两个条件的随机试验的概率模型称为古典概型 ①所有的基本事件只有有限个; ②每个基本事件的发生都是等可能的。 4.古典概型的概率: 如果一次试验的等可能基本事件共有个,那么每一个等可能基本事件发生的概率都是,如果某个事件包含了其中个等可能基本事件,那么事件发生的概率为. 例1.一个口袋内装有大小相同的5只球,其中3只白球,2只黑球,从中一次摸出两个球, (1)共有多少个基本事件? (2)摸出的两个都是白球的概率是多少? 例2、课本132例1
| 古典概型解题步骤: ⑴阅读题目,搜集信息; ⑵判断是否是等可能事件,并用字母表示事件; ⑶求出基本事件总数和事件所包含的结果数; ⑷用公式求出概率并下结论. 学生活动 把“抽到红心”记为事件,那么事件相当于“抽到红心1”,“抽到红心2”,…,“抽到红心”这13中情况,而同样抽到其他牌的共有种情况;由于是任意抽取的,可以认为这中情况的可能性是相等的。
一般用列举法列出所有基本事件的结果,画树状图是列举法的基本方法. 学 。X。X。 ]
| |
课堂检测内容 | 课本134页练习1.2.3.4 | |||
课后作业布置 | 课本147页1.2.3 | |||
预习内容布置 | 课本134—137页 | |||
北师大版必修32.2建立概率模型教案: 这是一份北师大版必修32.2建立概率模型教案,共2页。
高中北师大版1.2生活中的频率教案设计: 这是一份高中北师大版1.2生活中的频率教案设计,共2页。教案主要包含了第三章等内容,欢迎下载使用。
高中数学北师大版必修32.1古典概型的特征和概率计算公式教学设计及反思: 这是一份高中数学北师大版必修32.1古典概型的特征和概率计算公式教学设计及反思,共8页。













