高中数学人教A版 (2019)选择性必修 第三册8.3 分类变量与列联表集体备课课件ppt

这是一份高中数学人教A版 (2019)选择性必修 第三册8.3 分类变量与列联表集体备课课件ppt，共42页。PPT课件主要包含了新知探究，临界值，答案A，答案B等内容，欢迎下载使用。
山东省教育厅大力推行素质教育，增加了高中生的课外活动时间，某校调查了学生的课外活动方式，结果整理成下表：
问题　如何判定“喜欢体育还是文娱与性别是否有联系”？提示　可通过表格与图形进行直观分析，也可通过统计分析定量判断．
χ2 统计量也可以用来作相关性的度量．χ2 越小说明变量之间越独立，χ2越大说明变量之间越相关
2．独立性检验基于小概率值α的检验规则是：当χ2≥xα时，我们就推断H0不成立，即认为X和Y不独立，该推断犯错误的概率不超过α；当χ2＜xα时，我们没有充分证据推断H0不成立 ，可以认为X和Y独立．这种利用χ2的取值推断分类变量X和Y是否独立的方法称为χ2独立性检验，读作“卡方独立性检验”，简称独立性检验(test f independence)．
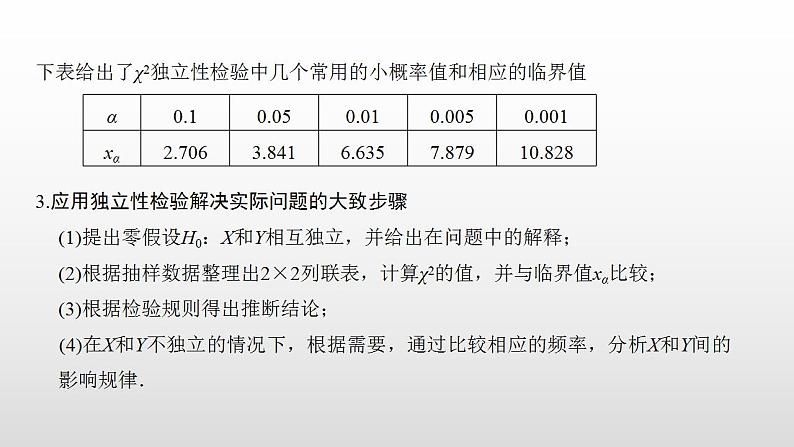
下表给出了χ2独立性检验中几个常用的小概率值和相应的临界值
3.应用独立性检验解决实际问题的大致步骤(1)提出零假设H0：X和Y相互独立，并给出在问题中的解释；(2)根据抽样数据整理出2×2列联表，计算χ2的值，并与临界值xα比较；(3)根据检验规则得出推断结论；(4)在X和Y不独立的情况下，根据需要，通过比较相应的频率，分析X和Y间的影响规律．
拓展深化[微判断]1．概率值α越小，临界值xα越大． ( )2．独立性检验的思想类似于反证法． ( )3．独立性检验的结论是有多大的把握认为两个分类变量有关系． ( )
[微训练]1．如果根据小概率α＝0.01的χ2检测试验，认为H0成立，那么具体算出的数据满足(　　)附表：
A.χ2＞6.635 B．χ2＞5.024C．χ2＞7.879 D．χ2＞3.841答案　A
2．某校为了研究“学生的性别”和“对待某一活动的态度”是否有关，运用2×2列联表进行独立性检验，经计算χ2＝7.069，则认为“学生性别与支持某项活动有关系”的犯错误的概率不超过(　　)A．0.1% B．1%C．99% D．99.9%
解析　∵χ2＝7.069>6.635＝x0.01，∴认为“学生性别与支持某项活动有关系”的犯错误的概率不超过1%.答案　B
[微思考]1．有人说：“在犯错误的概率不超过0.01的前提下认为吸烟和患肺病有关，是指每100个吸烟者中就会有99个患肺病的．”你认为这种观点正确吗？为什么？提示　观点不正确．犯错误的概率不超过0.01说明的是吸烟与患肺病有关的程度，不是患肺病的百分数．2．应用独立性检验的基本思想对两个变量间的关系作出的推断一定是正确的吗？提示　不一定．所有的推断只代表一种可能性，不代表具体情况．
题型一　有关“相关的检验”【例1】　某校对学生课外活动进行调查，结果整理成下表，用你所学过的知识进行分析，能否在犯错误的概率不超过0.005 的前提下，认为“喜欢体育还是文娱与性别有关系”？
解　零假设为H0：喜欢体育还是喜欢文娱与性别没有关系∵a＝21，b＝23，c＝6，d＝29，n＝79，
根据小概率值α＝0.005的χ2独立性检验，我们推断H0不成立，即认为喜欢体育还是喜欢文娱与性别有关系，此推断犯错误的概率不大于0.005.
【训练1】　打鼾不仅影响别人休息，而且可能与患某种疾病有关．下表是一次调查所得的数据：
根据独立性检验，能否在犯错误的概率不超过0.001的前提下认为每一晚都打鼾与患心脏病有关系？
解　零假设为H0：打鼾与患心脏病无关系由列联表中的数据，得
≈68.033>10.828＝x0.001.根据小概率值α＝0.001的χ2独立性检验，我们推断H0不成立，即认为打鼾与患心脏病有关系，此推断犯错误的概率不大于0.001.
题型二　有关“无关的检验”【例2】　为了探究学生选报文、理科是否与对外语的兴趣有关，某同学调查了361名高二在校学生，调查结果如下：理科生对外语有兴趣的有138人，无兴趣的有98人，文科生对外语有兴趣的有73人，无兴趣的有52人．试分析学生选报文、理科与对外语的兴趣是否有关？解　零假设为H0：选报文、理科与对外语的兴趣无关．列出2×2列联表
代入公式得χ2的观测值
∵1.871×10－4＜2.706＝x0.1，根据小概率值α＝0.1的χ2独立性检验，没有充分证据推断H0不成立，即选报文、理科与对外语的兴趣无关.
规律方法　独立性检验的关注点在2×2列联表中，如果两个分类变量没有关系，则应满足ad－bc≈0，因此|ad－bc|越小，关系越弱；|ad－bc|越大，关系越强．
【训练2】　某教育机构为了研究成年人具有大学专科以上学历(包括大学专科)和对待教育改革态度的关系，随机抽取了392名成年人进行调查，所得数据如下表所示：
解　零假设为H0：成年人具有大学专科以上学历(包括大学专科)和对待教育改革态度无关．根据表中数据，计算得
因为1.78