






人教版新课标B选修1-13.3.2利用导数研究函数的极值教案配套ppt课件
展开新知探求 素养养成
函数y=f(x)在区间[a,b]内的图象如图所示:
问题1:y=f(x)在x1,x2,x3,x4处的导数等于多少?答案:都等于零.问题2:在x=x1和x=x2附近两侧导数f′(x)的符号有什么特点?答案:f′(x)在x=x1左侧符号为正,右侧符号为负;在x=x2左侧符号为负,右侧符号为正.问题3:函数的极大值一定大于极小值吗?在区间内可导函数的极大值和极小值是否唯一?答案:函数的极大值不一定大于极小值,如图所示极大值f(x1)小于极小值f(x4).函数的极大值和极小值并不唯一如f(x1),f(x3)都是极大值;f(x2),f(x4)都是极小值.问题4:导数等于零的点一定是极值点吗?导数为零是该点为极值点的什么条件?答案:导数等于零的点不一定是极值点,如y=x3在x=0处的导数为零,但x=0不是极值点;极值点的导数一定为零,因此导数为零是该点为极值点的必要不充分条件.
梳理 1.函数的极小值与极小值点若函数f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点的函数值 ,且f′(a)=0,而且在x=a附近的左侧 ,右侧 ,则点a叫做函数的极小值点,f(a)叫做函数的极小值.2.函数的极大值与极大值点若函数f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点的函数值 ,且f′(b)=0,而且在x=b附近的左侧 ,右侧 ,则点b叫做函数的极大值点,f(b)叫做函数的极大值.
求定义域→求f′(x)→求方程f′(x)=0的根→列表检验f′(x)在f′(x)=0的根的附近两侧的符号→下结论.名师点津:(1)对于可导函数f(x),f′(x0)=0是函数f(x)在x=x0处有极值的必要不充分条件.(2)f′(x0)=0时,x0不一定是极值点.
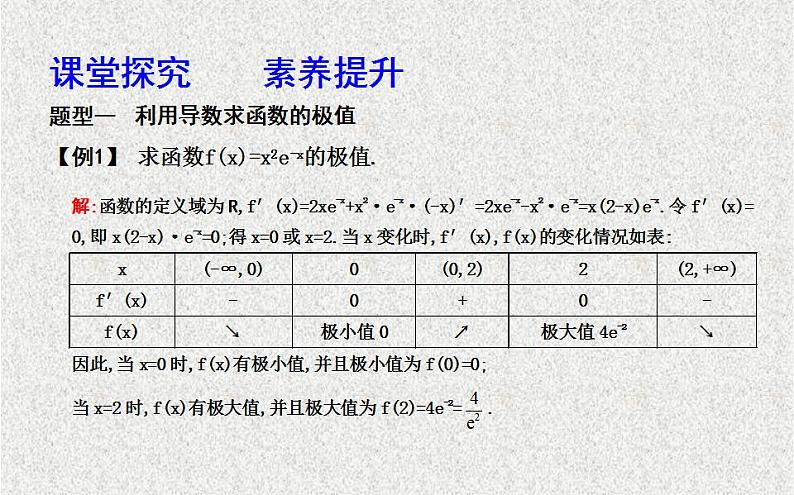
课堂探究 素养提升
【例1】 求函数f(x)=x2e-x的极值.
方法技巧 求可导函数f(x)的极值的步骤(1)确定定义域,求导函数f′(x);(2)求解不等式f′(x)>0得增区间,求解f′(x)<0得减区间,再判断f′(x) =0的解左右f′(x)的正负得极值点;(3)求出极值.
【例2】 (2017·马山县期末)设x=-2与x=4是函数f(x)=x3+ax2+bx的两个极值点.(1)求常数a,b;(2)判断x=-2,x=4是函数f(x)的极大值点还是极小值点,并说明理由.
解:(1)f′(x)=3x2+2ax+b.可知x=-2和x=4是方程f′(x)=0的两根,则a=-3,b=-24.(2)x=-2是f(x)的极大值点,x=4是f(x)的极小值点.理由如下:f′(x)=3(x+2)(x-4),得当x<-2时,f′(x)>0;当-2
方法技巧 已知函数的极值点,求参数问题的解题步骤(1)求函数的导数f′(x);(2)由极值点的导数为0,列出方程(组),求解参数.(3)当求出参数多于一组解时,一定要验证是否满足题目的条件.
即时训练2:(2016·四川卷)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5),[0.5,1),…,[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中a的值;(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
解:(1)由频率分布直方图,可知:月均用水量在[0,0.5)的频率为0.08×0.5=0.04.同理,在[0.5,1),[1.5,2),[2,2.5),[3,3.5),[3.5,4),[4,4.5]各组的频率分别为0.08,0.21,0.25,0.06,0.04,0.02.由1-(0.04+0.08+0.21+0.25+0.06+0.04+0.02)=0.5×a+0.5×a,解得a=0.30.(2)由(1)知,100位居民月均用水量不低于3吨的频率为0.06+0.04+0.02=0.12.由以上样本的频率分布,可以估计该市30万居民中月均用水量不低于3吨的人数为300 000×0.12=36 000.
(3)估计居民月均用水量的中位数.
解:(3)设中位数为x吨.因为前5组的频率之和为0.04+0.08+0.15+0.21+0.25=0.73>0.5,而前4组的频率之和为0.04+0.08+0.15+0.21=0.48<0.5,所以2≤x<2.5.由0.50×(x-2)=0.5-0.48,解得x=2.04.故可估计居民月均用水量的中位数为2.04吨.
【例3】 a为何值时,方程x3-3x2-a=0恰有一个实根、两个不等实根、三个不等实根,有没有可能无实根?
解:令f(x)=x3-3x2,y=a.f(x)的定义域为R.方程x3-3x2-a=0的根的个数即x3-3x2=a根的个数,f(x)=x3-3x2与y=a交点个数.由f′(x)=3x2-6x=0.得x=0或x=2,所以当x<0或x>2时,f′(x)>0;当0
即时训练3:(2018·郑州高二监测)已知函数f(x)的定义域为[-1,5],部分对应值如表:
f(x)的导函数y=f′(x)的图象如图所示.(1)f(x)的极小值为 ;
(2)若函数y=f(x)-a有4个零点,则实数a的取值范围为 .
解析:(2)y=f(x)的图象如图所示:若函数y=f(x)-a有4个零点,则a的取值范围为1≤a<2.答案:(2)[1,2)
易错辨析——忽视函数极值存在的条件致误
【例4】 (2018·贵阳高二检测)已知函数f(x)=x3+3mx2+nx+m2在x=-1时有极值0,则m+n= .
纠错:导数等于零的点不一定是函数的极值点,需要判断f′(x)在该点左右两侧的符号是否相反.
高中数学人教版新课标B选修1-13.3.3导数的实际应用评课ppt课件: 这是一份高中数学人教版新课标B选修1-13.3.3导数的实际应用评课ppt课件,共36页。PPT课件主要包含了答案B,答案4,方法技巧等内容,欢迎下载使用。
数学选修1-13.3.3导数的实际应用授课ppt课件: 这是一份数学选修1-13.3.3导数的实际应用授课ppt课件,共30页。PPT课件主要包含了解析答案,反思与感悟,此时y′0,分类讨论思想的应用,解后反思,答案D等内容,欢迎下载使用。
高中数学人教版新课标B选修1-13.3.2利用导数研究函数的极值课前预习ppt课件: 这是一份高中数学人教版新课标B选修1-13.3.2利用导数研究函数的极值课前预习ppt课件,共30页。PPT课件主要包含了极值点,端点处,最大值,最小值,解析答案,反思与感悟,解后反思,分类讨论思想的应用,解得0<a<e,-71等内容,欢迎下载使用。













